- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Критические точки функции, максимумы и минимумы , 10 класс.
Содержание
- 1. Презентация: Критические точки функции, максимумы и минимумы , 10 класс.
- 2. Эпиграф. “При изучении наук примеры не менее
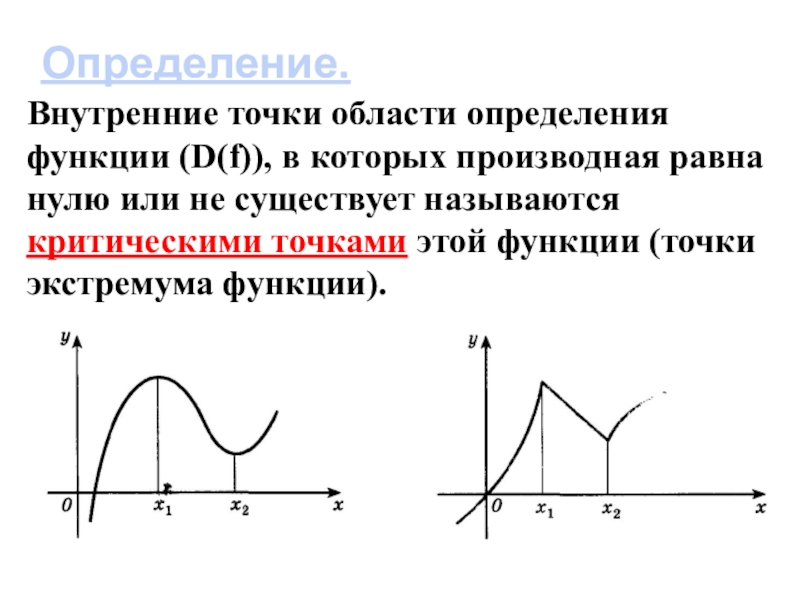
- 3. Определение.Внутренние точки области определения функции (D(f)), в
- 4. Теорема Ферма (необходимое условие экстремума)
- 5. Пьер де Ферма́ (фр. Pierre de Fermat,
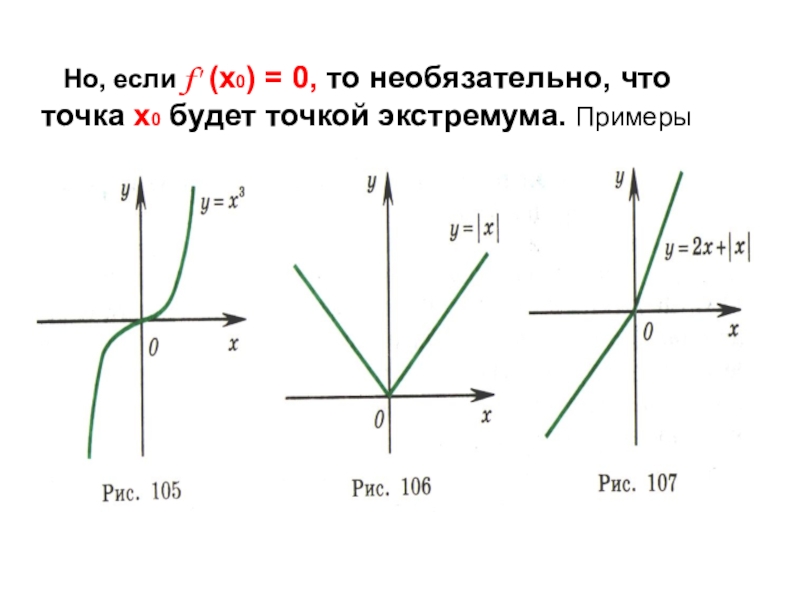
- 6. Но, если f' (х0) =
- 7. Признак максимума функции.x0maxxf′(x)f(x)+ - ba
- 8. x0minxf′(x)f(x)- + Признак минимума функции.ab
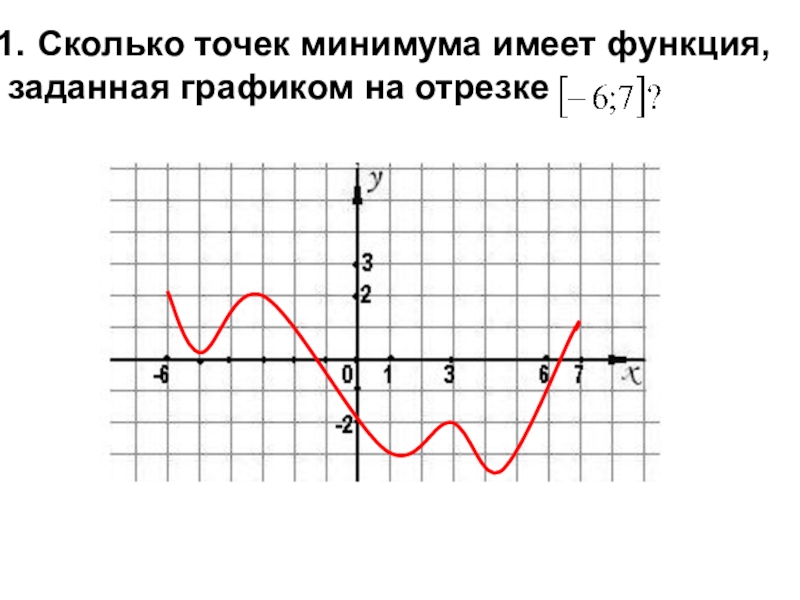
- 9. № 1.Найдите точки экстремума и экстремумы функции: f(x)=3x-x3.
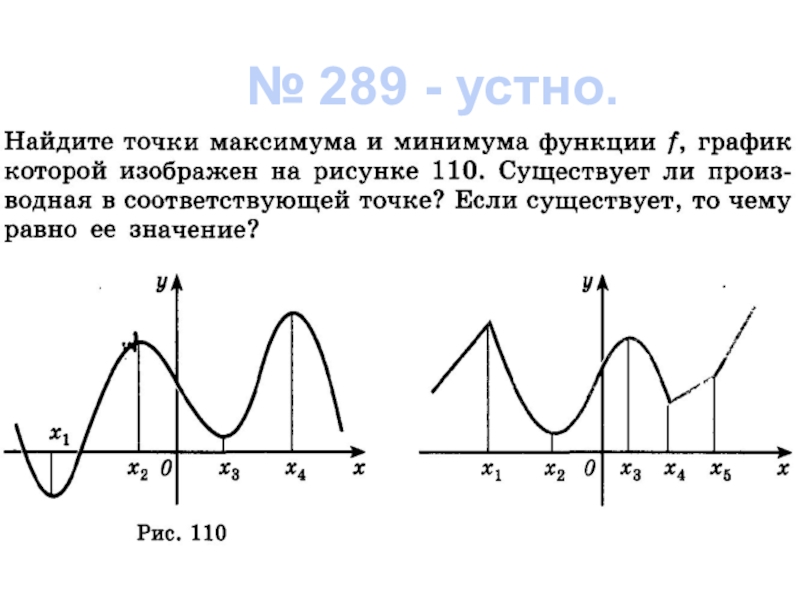
- 10. № 289 - устно.
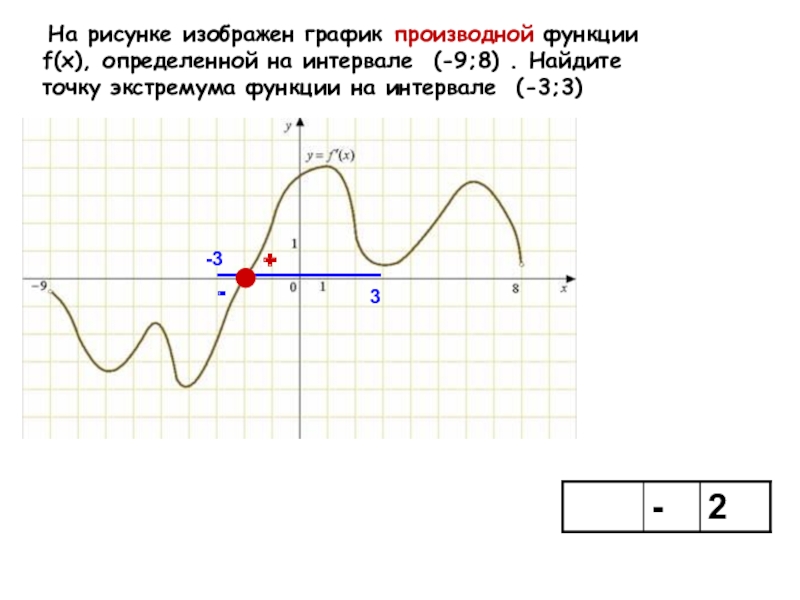
- 11. На рисунке изображен график производной функции f(x),
- 12. Слайд 12
- 13. На рисунке изображен график функции y=f(x)
- 14. Домашняя работа.№ 288 (в;г) 290 (б;в).
Эпиграф. “При изучении наук примеры не менее поучительны, нежели правила”. “Примеры учат больше, чем теория”. ( И. Ньютон , М. Ломоносов )
Слайд 2Эпиграф.
“При изучении наук примеры не менее поучительны, нежели правила”.
“Примеры
учат больше, чем теория”.
( И. Ньютон , М. Ломоносов )
( И. Ньютон , М. Ломоносов )
Слайд 3Определение.
Внутренние точки области определения функции (D(f)), в которых производная равна нулю
или не существует называются критическими точками этой функции (точки экстремума функции).
Слайд 5Пьер де Ферма́ (фр. Pierre de Fermat, 17 августа 1601 —
12 января 1665) — французский математик, один из создателей аналитической геометрии, математического анализа, теории вероятностей и теории чисел. По профессии юрист, с 1631 года — советник парламента в Тулузе. Блестящий полиглот. Наиболее известен формулировкой Великой теоремы Ферма.
Слайд 11 На рисунке изображен график производной функции f(x), определенной на интервале (-9;8)
. Найдите точку экстремума функции на интервале (-3;3)
-3
3
+
-
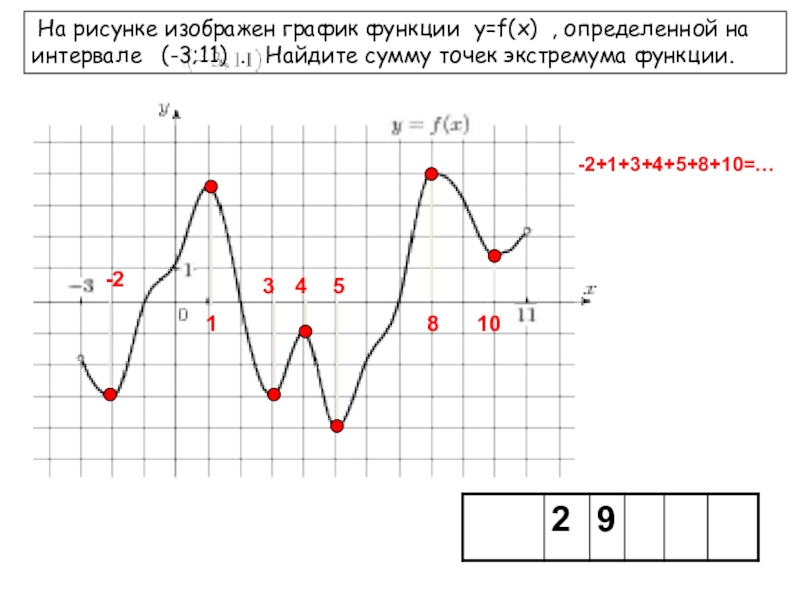
Слайд 13 На рисунке изображен график функции y=f(x) , определенной на интервале
(-3;11) . Найдите сумму точек экстремума функции.
3
-2+1+3+4+5+8+10=…