- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад конкурса по математике, 7 класс
Содержание
- 1. Презентация конкурса по математике, 7 класс
- 2. Первый тур20 минут
- 3. Натуральное число a увеличили на 1, при
- 4. Решение задачи №1(5 баллов)Ответ: 1009.Решение. (а+1)2-а2=2019,
- 5. Задача №2Вася получил список книг на летние
- 6. Решение задачи №2(5 баллов) Ответ: на две
- 7. Решение задачи №2(5 баллов) Ответ: на две
- 8. Задача №3Сумма двух сторон прямоугольника равна
- 9. Решение задачи №3(5 баллов). .Ответ: 12 см или
- 10. Второй тур20 минут
- 11. Задача №1Простым или составным является число 1002 + 201?
- 12. Решение задачи №1(6 баллов) Ответ: составным.
- 13. Задача №2В разноцветной семейке было поровну
- 14. Решение задачи №2(6 баллов) ..
- 15. Задача №3Дана последовательность, в которой пропущено
- 16. Решение задачи №3(6 баллов) Ответ:
- 17. Третий тур25 минут
- 18. Задача №1Вася увидел в музее странные
- 19. Решение задачи №1(7 баллов) Ответ:
- 20. Задача №2На середине дороги от Васиного
- 21. Решение задачи №2(7 баллов)Ответ: 20 минут.Решение.
- 22. Задача №3На стороне ВС треугольника АВС
- 23. Решение задачи №3(7 баллов) Решение. Так
- 24. Маршрут пройден. Спасибо всем за участие в регате!!!
Первый тур20 минут
Слайд 3Натуральное число a увеличили на 1, при этом его квадрат увеличился
на 2019. Чему равно a?
Задача №1
Слайд 5Задача №2
Вася получил список книг на летние каникулы (12 недель). Он
поставил себе цель их прочитать и решил, что каждую неделю он будет читать одно и то же количество книг. Но каждую неделю Вася читал на одну книгу меньше запланированного, поэтому выполнил свой план на 3 недели позже, чем хотел. На сколько недель раньше срока Вася прочитал бы весь список, если бы каждую неделю читал на одну книгу больше, чем планировал?
.
.
Слайд 6Решение задачи №2
(5 баллов)
Ответ: на две недели.
Решение. Первый способ
За 12 недель Вася не успел прочитать 12 книг. Их он прочитает за 3 недели, то есть Вася в реальности читал по 4 книги в неделю, а планировал читать по 5 книг. Следовательно, в списке – 60 книг. Если бы он читал по 6 книг в неделю, то справился бы за 10 недель, то есть на две недели раньше срока.
.
Слайд 7Решение задачи №2
(5 баллов)
Ответ: на две недели.
Решение. Второй способ
Пусть Вася хотел читать по х книг в неделю, тогда в его списке – 12x книг. В реальности, он каждую неделю читал х – 1 книгу и потратил на это 15 недель, то есть в списке 15(х – 1) книг. Таким образом, 12x = 15(х – 1), откуда x = 5. Значит, в списке – 60 книг. Поэтому если читать по 6 книг в неделю, то хватит 60 : 6 = 10 недель, то есть Вася прочитал бы весь список на 12 – 10 = 2 недели раньше окончания каникул.
Слайд 8
Задача №3
Сумма двух сторон прямоугольника равна 7 см, а сумма
трёх его сторон равна 9,5 см. Найдите периметр прямоугольника.
Слайд 9Решение задачи №3
(5 баллов)
.
.
Ответ: 12 см или 13 см или 14
см.
Решение. Пусть а и b – длины сторон прямоугольника, тогда Р = 2(а + b) – его периметр. По условию: 2а + b = 9,5. Далее возможны три случая:
1) 2а = 7, тогда а = 3,5; b = 2,5; Р = 12 (см).
2)2b = 7, тогда b = 3,5; а = 3; Р = 13 (см).
3) а + b = 7, тогда а = 2,5; b = 4,5; Р = 14 (см).
Решение. Пусть а и b – длины сторон прямоугольника, тогда Р = 2(а + b) – его периметр. По условию: 2а + b = 9,5. Далее возможны три случая:
1) 2а = 7, тогда а = 3,5; b = 2,5; Р = 12 (см).
2)2b = 7, тогда b = 3,5; а = 3; Р = 13 (см).
3) а + b = 7, тогда а = 2,5; b = 4,5; Р = 14 (см).
Слайд 12
Решение задачи №1
(6 баллов)
Ответ: составным.
Решение.
1002 + 201
= 1002 + 2100 + 1 = (100 + 1)2 = 1012.
Следовательно, данное число делится на 101,
то есть оно составное.
Следовательно, данное число делится на 101,
то есть оно составное.
Слайд 13
Задача №2
В разноцветной семейке было поровну белых, синих и полосатых
детей-осьминожков. Когда несколько синих осьминожков стали полосатыми, папа решил посчитать детей. Синих и белых вместе взятых оказалось 10, зато белых и полосатых вместе взятых — 18. Сколько детей в разноцветной семейке?
Слайд 14Решение задачи №2
(6 баллов)
.
.
Ответ. 21.
Первое решение. Заметим, что белых осьминожков было треть от общего количества, и они не перекрашивались. Если сложить 10 и 18, то получится количество всех детей вместе, к которому прибавлено количество белых, то есть 4/3 от количества всех детей. Значит, 4/3 от количества детей в семейке равно 28, то есть всего детей 21.
Второе решение. После перекрашивания полосатых осьминожков стало на 18 − 10 = 8 больше, чем синих. Значит, полосатыми стали 8 : 2 = 4 синих осьминожка. Белых и «старых полосатых» было 18 − 4 = 14, то есть по 14 : 2 = 7 каждого цвета. А всего в разноцветной семейке 3 · 7 = 21 ребёнок.
Слайд 15
Задача №3
Дана последовательность, в которой пропущено ровно пять чисел:
102;
105; 111; 114; 120; 123; 129; ___; ___; ___; ___; ___; 201; 204; 210; 213; 219.
Вставьте пропущенные числа.
Вставьте пропущенные числа.
Слайд 16
Решение задачи №3
(6 баллов)
Ответ: пропущены числа 141; 147;
159; 174; 186.
Решение: Для того, чтобы восстановить пропущенные числа, необходимо заметить, что каждый член данной последовательности, начиная со второго, получается в результате сложения предыдущего члена и суммы его цифр: 111 = 105 + 6; 114 = 111 + 3; и т. д. Искомые числа: 141 = 129 + 12; 147 = 141 + 6; 159 = 147 + 12; 174 = 159 + 15; 186 = 174 + 12.
Решение: Для того, чтобы восстановить пропущенные числа, необходимо заметить, что каждый член данной последовательности, начиная со второго, получается в результате сложения предыдущего члена и суммы его цифр: 111 = 105 + 6; 114 = 111 + 3; и т. д. Искомые числа: 141 = 129 + 12; 147 = 141 + 6; 159 = 147 + 12; 174 = 159 + 15; 186 = 174 + 12.
Слайд 18
Задача №1
Вася увидел в музее странные часы (см. рисунок). Они
отличаются от обычных часов тем, что на их циферблате нет цифр и вообще непонятно, где у часов верх; да ещё секундная, минутная и часовая стрелки имеют одинаковую длину. Какое время показывали часы? (Стрелки А и Б на рисунке смотрят ровно на часовые отметки, а стрелка В чуть-чуть не дошла до часовой отметки.)
Слайд 19
Решение задачи №1
(7 баллов)
Ответ: Без десяти пять.
Решение.
Подумаем, какая из стрелок часовая. Если бы часовая стрелка смотрела ровно на часовую отметку, минутная и секундная стрелка смотрели бы ровно на отметку «12» — но на картинке нет совпадающих стрелок. Значит, часовая стрелка — стрелка В. Оставшиеся 2 стрелки указывают ровно на часовые отметки, поэтому сейчас сколько-то часов и целое число минут — в частности, секундная стрелка указывает на 12. Если секундная стрелка — стрелка А, то на часах немного меньше семи часов (судя по часовой стрелке), а с другой стороны — сейчас на 10 минут больше, чем сколько-то часов (судя по минутной). Так быть не может. Если же секундная стрелка — стрелка Б, то на часах около пяти часов (судя по часовой стрелке), а судя по минутной стрелке — на 10 минут меньше, чем сколько-то часов. Значит, на часах без десяти пять.
Слайд 20
Задача №2
На середине дороги от Васиного дома до школы стоит
светофор. В понедельник Вася попал на зеленый сигнал светофора. Во вторник он шел с той же скоростью, но простоял на светофоре 5 минут, а после этого увеличил скорость вдвое. И в понедельник, и во вторник он потратил на путь от дома до школы одинаковое время. Какое?
Слайд 21
Решение задачи №2
(7 баллов)
Ответ: 20 минут.
Решение. Пусть в понедельник Вася
шел со скоростью v м/мин и затратил на путь от дома до школы 2t минут, тогда длина половины пути от дома до школы равна vt метров. Во вторник, вторую половину пути Вася шел со скоростью 2v м/мин и затратил на 5 минут меньше, то есть (t – 5) минут. Следовательно, , откуда t = 10.
Слайд 22
Задача №3
На стороне ВС треугольника АВС отмечена точка E, а
на биссектрисе BD – точка F, таким образом, что EF || AC и AF = AD. Докажите, что AВ = ВЕ.
Слайд 23
Решение задачи №3
(7 баллов)
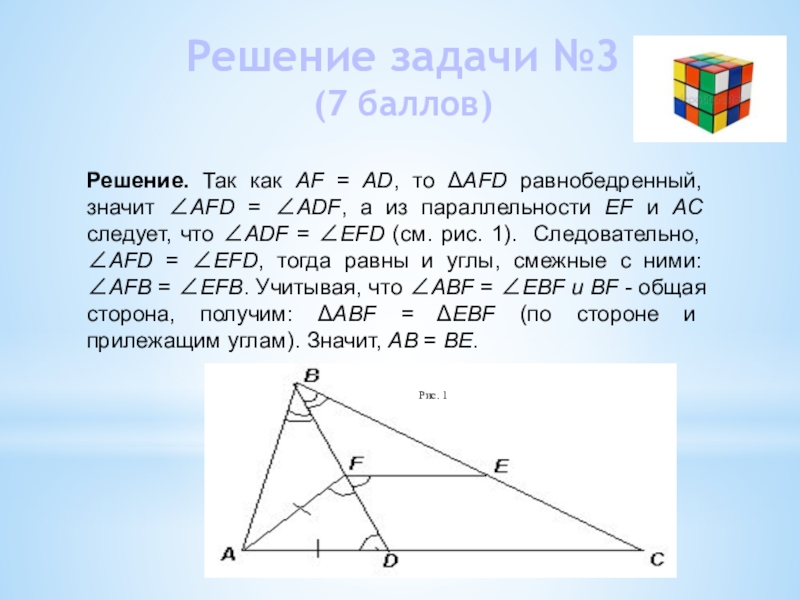
Решение. Так как AF = AD,
то АFD равнобедренный, значит АFD = АDF, а из параллельности EF и AC следует, что АDF = ЕFD (см. рис. 1). Следовательно, АFD = ЕFD, тогда равны и углы, смежные с ними: АFВ = ЕFВ. Учитывая, что АВF = ЕВF и BF - общая сторона, получим: АВF = ЕВF (по стороне и прилежащим углам). Значит, AВ = ВЕ.