- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку: Тригонометрические упражнения.
Содержание
- 1. Презентация к уроку: Тригонометрические упражнения.
- 2. Цель изучения темы: Изучить понятие обратной функции,
- 3. Арксинус и его свойстваАрксинусом числа a (|a|≤1)
- 4. Область опрделения функции y = arcsin x
- 5. Арккосинус и его свойстваАрккосинусом числа a (|a|≤1)
- 6. Область опрделения функции y = arccos x
- 7. Уравнение sin t = a0xy2. Отметить точку
- 8. Частные случаи уравнения sin t = axysint = 0sint = -1sint = 1
- 9. Уравнение cos t = a0xy2. Отметить точку
- 10. Частные случаи уравнения cos t = axyсos t = 0сos t = -1сos t = 1
- 11. Примеры уравнений0xy-11cos x = ½
- 12. Неравенство cos t > a0xy1. Отметить на
- 13. Неравенство cos t ≤ a0xy1. Отметить на
- 14. Неравенство sin t > a0xy1. Отметить на
- 15. Неравенство sin t ≤ a0xy1. Отметить на
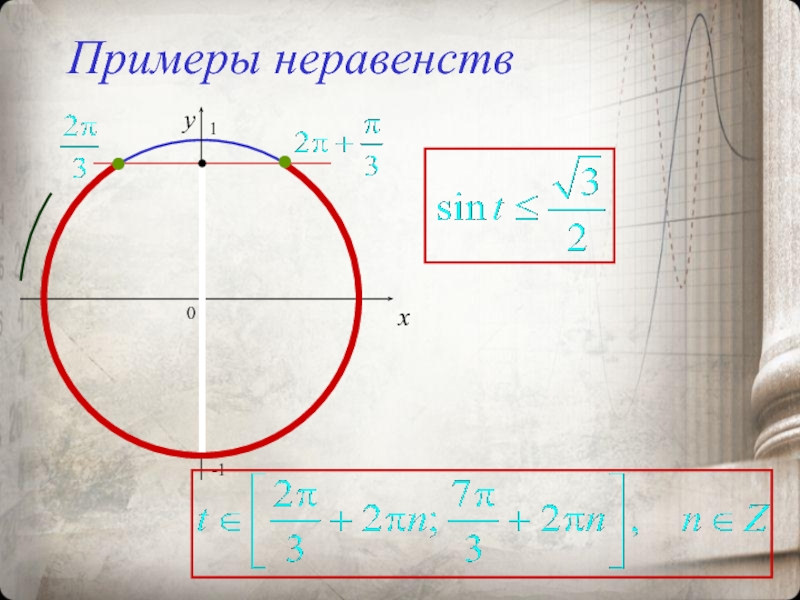
- 16. Примеры неравенств0xy-11
- 17. Спасибо за внимание!
Слайд 2
Цель изучения темы:
Изучить понятие обратной функции, обратных тригонометрических функций. Рассмотреть
Ввести понятие тригонометрического уравнения и неравенства.
Научиться решать простейшие уравнения и неравенства и отдельные виды тригонометрических уравнений, которые приводятся к простейшим.
Знать:
формулы общего решения простейших тригонометрических уравнений
Уметь:
решать тригонометрические уравнения, простейшие тригонометрические неравенства
Слайд 3Арксинус и его свойства
Арксинусом числа a (|a|≤1) называется такой угол α,
Обозначается этот угол arcsin a. Читается так: угол, синус которого равен a .
![Арксинус и его свойстваАрксинусом числа a (|a|≤1) называется такой угол α, принадлежащий отрезку [-π/2; π/2], синус которого](/img/thumbs/4cd02f3fd807df0ccdbce33bee31dedc-800x.jpg "Презентация к уроку: Тригонометрические упражнения. Арксинус и его свойстваАрксинусом числа a (|a|≤1) называется такой угол α,")
Слайд 4Область опрделения функции y = arcsin x – отрезок [-1;1]
Область значений
График функции y = arcsin x симметричен графику функции y = sin x, относительно прямой y = x.
![Область опрделения функции y = arcsin x – отрезок [-1;1]Область значений – отрезок [-π/2; π/2].График функции y](/img/thumbs/c464c51673db03ddcac2a464d10359e8-800x.jpg "Презентация к уроку: Тригонометрические упражнения. Область опрделения функции y = arcsin x – отрезок [-1;1]Область значений")
Слайд 5Арккосинус и его свойства
Арккосинусом числа a (|a|≤1) называется такой угол α,
Обозначается этот угол arccos a. Читается так: угол, косинус которого равен a .
![Арккосинус и его свойстваАрккосинусом числа a (|a|≤1) называется такой угол α, принадлежащий отрезку [0; π], косинус которого](/img/thumbs/f195850cb11ee86ec2e6227dcdce5f65-800x.jpg "Презентация к уроку: Тригонометрические упражнения. Арккосинус и его свойстваАрккосинусом числа a (|a|≤1) называется такой угол α,")
Слайд 6Область опрделения функции y = arccos x – отрезок [-1;1]
Область значений
График функции y = arccos x симметричен графику функции y = cos x, относительно прямой y = x
![Область опрделения функции y = arccos x – отрезок [-1;1]Область значений – отрезок [0; π].График функции y](/img/thumbs/08c1b4618d7a6a63b9e496c8aff510df-800x.jpg "Презентация к уроку: Тригонометрические упражнения. Область опрделения функции y = arccos x – отрезок [-1;1]Область значений")
Слайд 7Уравнение sin t = a
0
x
y
2. Отметить точку а на оси ординат.
3.
4. Отметить точки пересечения перпендикуляра с окружностью.
5. Полученные точки – решение уравнения sint = a.
6. Записать общее решение уравнения.
1. Проверить условие | a | ≤ 1
a
t1
-t1
-1
1
t =
Слайд 9Уравнение cos t = a
0
x
y
2. Отметить точку а на оси абсцисс.
3.
4. Отметить точки пересечения перпендикуляра с окружностью.
5. Полученные точки – решение уравнения cost = a.
6. Записать общее решение уравнения.
1. Проверить условие | a | ≤ 1
a
t1
-t1
-1
1
t = ± arccos a +2πn; nєZ
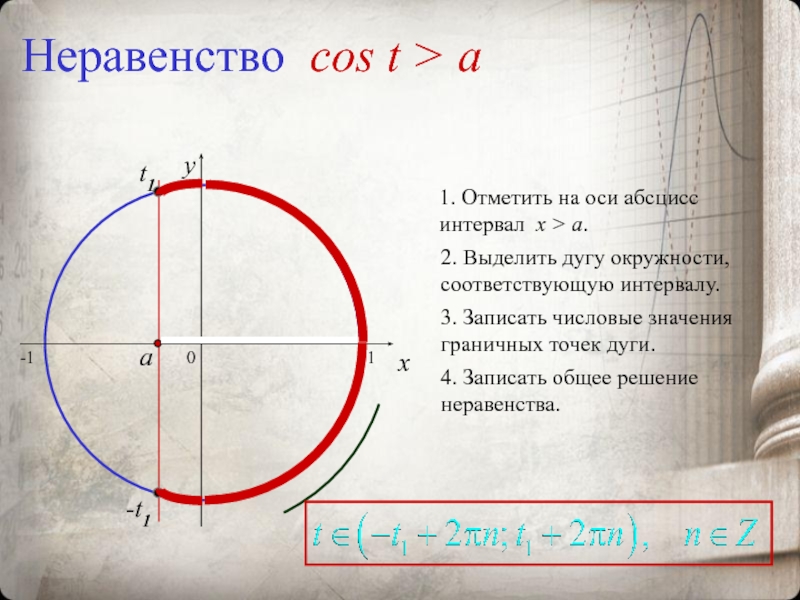
Слайд 12Неравенство cos t > a
0
x
y
1. Отметить на оси абсцисс интервал x
2. Выделить дугу окружности, соответствующую интервалу.
3. Записать числовые значения граничных точек дуги.
4. Записать общее решение неравенства.
a
t1
-t1
-1
1
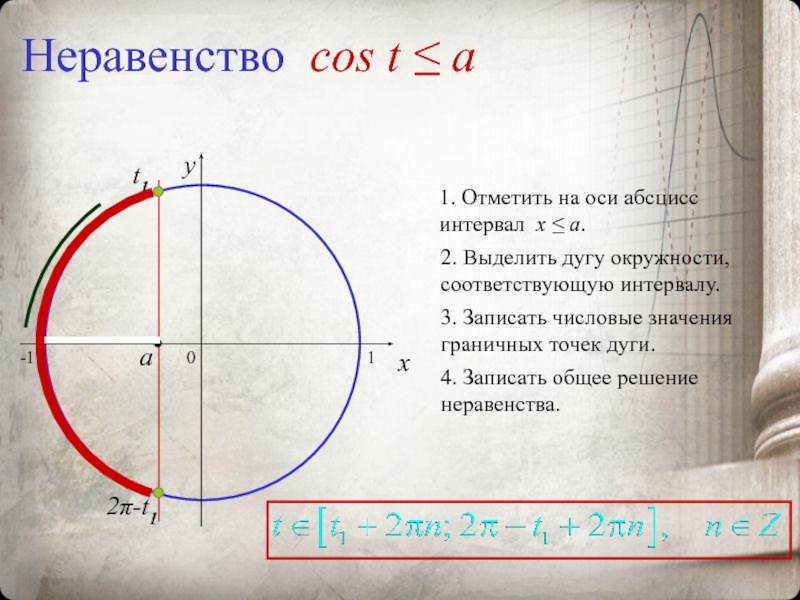
Слайд 13Неравенство cos t ≤ a
0
x
y
1. Отметить на оси абсцисс интервал x
2. Выделить дугу окружности, соответствующую интервалу.
3. Записать числовые значения граничных точек дуги.
4. Записать общее решение неравенства.
a
t1
2π-t1
-1
1
Слайд 14Неравенство sin t > a
0
x
y
1. Отметить на оси ординат интервал y
2. Выделить дугу окружности, соответствующую интервалу.
3. Записать числовые значения граничных точек дуги.
4. Записать общее решение неравенства.
a
t1
π-t1
-1
1
Слайд 15Неравенство sin t ≤ a
0
x
y
1. Отметить на оси ординат интервал y≤a.
2.
3. Записать числовые значения граничных точек дуги.
4. Записать общее решение неравенства.
a
3π-t1
t1
-1
1
