- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Тригонометрические функции. Формулы тригонометрии. 10 класс
Содержание
- 1. Презентация к уроку Тригонометрические функции. Формулы тригонометрии. 10 класс
- 2. Цели урока:Закрепление материала по теме «Тригонометрические функции,
- 3. История тригонометрииЗарождение тригонометрии относится к глубокой древности.
- 4. Может ли синус равняться:
- 5. 185° 102°- 102° 250°- 250°6.
- 6. sin128° > 0cos212° >0tg365° > 0 ctg290°
- 7. 1. sinα > 0
- 8. 1.sin213°tg46°cos389° 2.cos819°sin119°tg512° 3. tg212°cos200°sin89° 4. cos72°sin179°cos600°Определите знак выражения:
- 9. 7. tg90° не сущ. 8.
- 10. 2cos0° - 4sin90° + 5tg180° 2ctg90°
- 11. Продолжите равенство: sin(-α) =
- 12. 120°=135°=240°=150°=1. 3π/4=2. 5π/3=3. 7π/6=4. 2π/3=Перевести градусы в радианы, а радианы в градусы:
- 13. 2sinπ/3 + tgπ/4sin(-π) – cos(-3π/2)
- 14. .Найдите :sinα, tgα, ctgα, если cosα= - 5/13π/2
- 15. Слайд 15
- 16. cos²α – ( ctg²α + 1)sin²αsin⁴α +
- 17. sin(π/2 – α) 6. sin(270°
- 18. Вычислите:tg225°cos330°ctg120°sin240°( 3 балла)Упростите выражение:1.tg (3π/2-α)tg(π-α) - sin(2π-α)cos(3π/2-α)
- 19. Формулы тригонометрииcos107°cos17 + sin107°sin17° = cos90°=0sin63°cos27° +
- 20. С п а с и б о
Слайд 1Тема урока:
«Тригонометрические функции. Основные тригонометрические формулы.»
МКОУ «Захаровская СОШ»
Клетского района Волгоградской области
Могутова
Слайд 2Цели урока:
Закрепление материала по теме «Тригонометрические функции, формулы тригонометрии»;
Проверка знаний в
Развитие внимания, логического мышления, навыков контроля и самоконтроля;
Воспитание серьезного отношения к учебному труду.
»
Слайд 3История тригонометрии
Зарождение тригонометрии относится к глубокой древности. Само название «тригонометрия» греческого
Одним из основоположников тригонометрии считается древнегреческий астроном Гиппарх, живший во 2 веке до нашей эры. Гиппарх (Hípparchos) (около 180—190 до н. э., Никея, — 125 до н. э., Родос), древнегреческий учёный
Гиппарх является автором первых тригонометрических таблиц и одним из основоположников астрономии.
Слайд 4
Может ли синус равняться:
a)√2 б)
Найдите наибольшее и наименьшее
значение:
а) 1 + 3sinα б) 2 - cosα
Значения тригонометрических функций.
Слайд 5
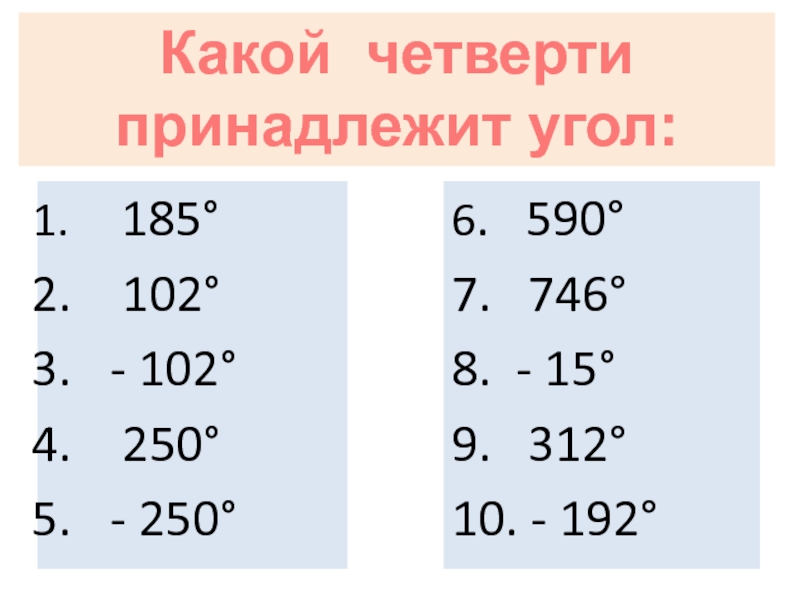
185°
102°
- 102°
250°
- 250°
6. 590°
7. 746°
8. -
9. 312°
10. - 192°
Какой четверти принадлежит угол:
Слайд 6
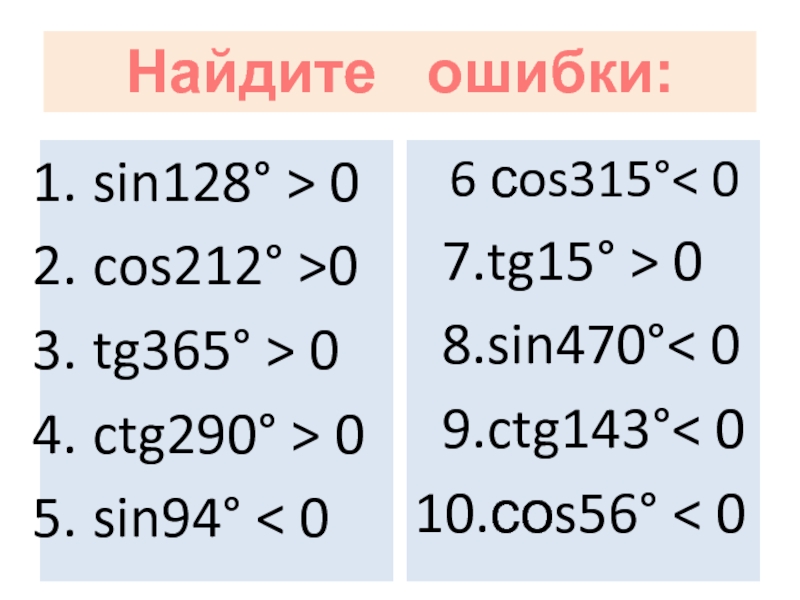
sin128° > 0
cos212° >0
tg365° > 0
ctg290° > 0
sin94° < 0
6
7.tg15° > 0
8.sin470°< 0
9.ctg143°< 0
10.соs56° < 0
Найдитe ошибки:
Слайд 7
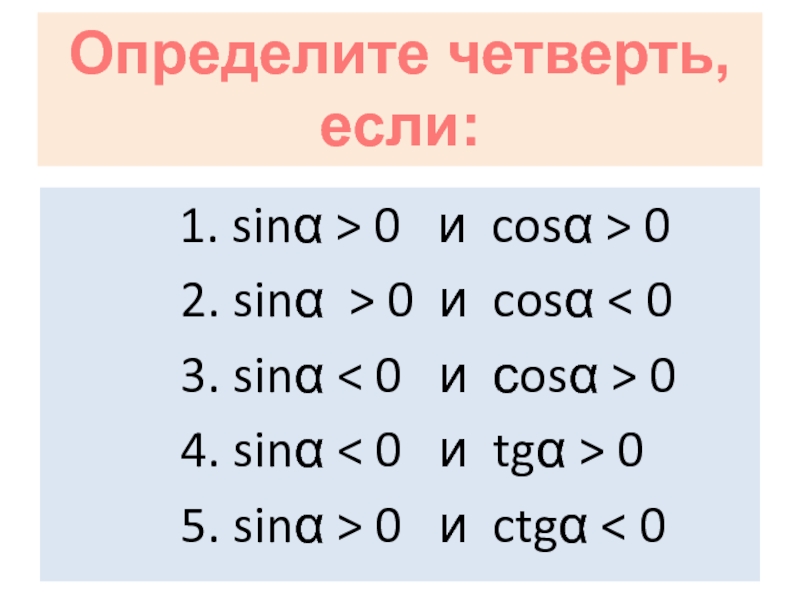
1. sinα > 0 и cosα >
2. sinα > 0 и cosα < 0
3. sinα < 0 и сosα > 0
4. sinα < 0 и tgα > 0
5. sinα > 0 и ctgα < 0
Определите четверть,
если:
Слайд 8
1.sin213°tg46°cos389°
2.cos819°sin119°tg512°
3. tg212°cos200°sin89°
Определите знак выражения:
Слайд 9
7. tg90° не сущ.
8. cos270°= 0
9. ctg60
10. sin90° = 1
tg45° = 1
cos180° = -1
sin60° = √3/2
cos90° = 0
tg180°= 0
ctg30° = √3
sin270° = -1
cos45° = √2/2
Знание табличных значений:
Слайд 10
2cos0° - 4sin90° + 5tg180°
2ctg90° - 3cos270° + 5sin180°
4sin90° - 3cos180°
8cos90° + 7sin360° + 12tg180°
Найдите значение выражения:
Слайд 11
Продолжите равенство:
sin(-α) = -sinα
cos(-α) = cosα ctg(-α) = - ctgα
Найдите значение:
1. sin(-30°) = - 1/2 4. ctg(-30°)= - √3
2. cos(-60°) = 1/2 5. sin(-90°) = - 1
3. tg(-45°) = -1 6. cos(-180°) = -1
Четность функций.
Слайд 12
120°=
135°=
240°=
150°=
1. 3π/4=
2. 5π/3=
3. 7π/6=
4. 2π/3=
Перевести градусы в радианы, а радианы
Слайд 13
2sinπ/3 + tgπ/4
sin(-π) – cos(-3π/2) + 2sin2π – tgπ
2sinπ
3sin2,5π + 2tg(-π/4) + cos4,5π
6sin13π/6 – 7cos13π/3 – tg(-17π/4)
3sin²π/2 – 4tg²π/4 -3cos²π/6
Вычислите:
Слайд 14
.
Найдите :
sinα, tgα, ctgα,
если
cosα= - 5/13
π/2
если
tgα= 2
π<α<3π/2
Основные тригонометрические формулы.
Слайд 15
1.
2. sin²α + cos²α + tg²α
3. tgαctgα + ctg²α
4. 1 – cos²α - sin²α
5. (sinα + cosα)² - 2sinαcosα
6. sin²α – tgαctgα
7. sinαctgα cosαtgα
8. 2sin²αcos²α + sin⁴α + cos⁴α
Упростите выражение:
Слайд 16
cos²α – ( ctg²α + 1)sin²α
sin⁴α + cos⁴α + 2sin²αcos²α
cos²tg²(-α) –
Докажите тождество:
(tgα + ctgα)² - (tgα – ctgα)² = 4
sin²αcos²β – cos²αsin²β = sin²α - sin²β
Тригонометрические формулы.
Слайд 17
sin(π/2 – α) 6. sin(270° - α)
cos(3π/2 –α)
tg(π + α) 8. cos(π – α)
cos(2π –α) 9. ctg(90°- α)
ctg(π/2 + α) 10. sin(180°+α)
Замените функцией угла α :
Слайд 18Вычислите:
tg225°cos330°ctg120°sin240°( 3 балла)
Упростите выражение:
1.tg (3π/2-α)tg(π-α) - sin(2π-α)cos(3π/2-α) +
+cos²(π/2-α) (1 балл)
2.ctg(π-α)ctg(3π/2+α) +
3.sin(90°-α)+cos(180°+α)+tg(270°+α) ( 1 балл)
(
Формулы приведения.
Слайд 19Формулы тригонометрии
cos107°cos17 + sin107°sin17° = cos90°=0
sin63°cos27° + cos63°sin27°= sin90°=1
2sin15°cos15°= sin30°=1/2
8sinπ/8cosπ/8 =4sinπ/4=2√2
2cos²15°
cos²22,5° – sin²22,5° = cos45°= √2/2
sin15°cos15 = 1/2sin30° = 1/4