Презентация, доклад к уроку Свойства степени с натуральным показателем

Содержание

1. Презентация к уроку Свойства степени с натуральным показателем
2. «Пусть кто-нибудьпопробует вычеркнутьиз математики степени, и он
3. Цели урока:Общеобразовательные: – знакомство со свойством возведения
4. Закончите фразу1) Произведение n множителей, каждый из
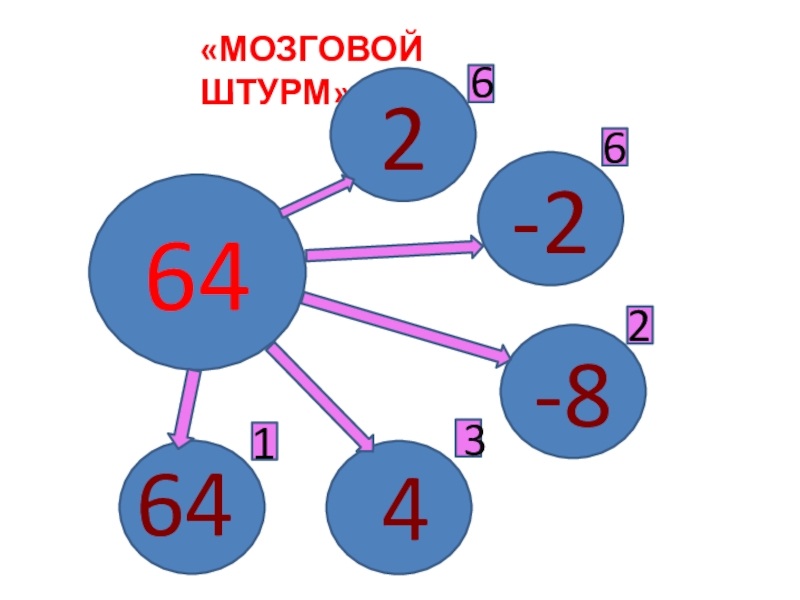
5. «МОЗГОВОЙ ШТУРМ»642-2-836624164
6. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА(25)2 =25•25=25+5=210(32)3 =32•32•32=32+2+2=36(а n) m=
7. Представьте в виде степени1) (32)5 = 2)
8. Си́мон Сте́вин (нидерл. Simon Stevin, 1548—1620) —
9. Современная запись показателя степени введена Декартом в
10. 1. Запишите в виде степени с основанием
11. Вариант 1.
12. Рефлексия
13. Домашнее задание1.Выучить свойства степени с доказательством2.Заполните свободные
14. СПАСИБО ЗА УРОК!!!

«Пусть кто-нибудьпопробует вычеркнутьиз математики степени, и он увидит, чтобез них далеко не уедешь.» М.В. Ломоносов

Главная
Алгебра
Презентация к уроку Свойства степени с натуральным показателем

Слайд 1Свойства степени с
натуральным показателем

Слайд 2«Пусть кто-нибудь
попробует вычеркнуть
из математики степени,
и он увидит, что
без них далеко

не уедешь.»
М.В. Ломоносов

Слайд 3Цели урока:
Общеобразовательные: – знакомство со свойством возведения степени в степень,
отработка

умений систематизировать, обобщать знания о степени с натуральным
показателем, закрепить и усовершенствовать навыки простейших преобразований
выражений, содержащих степени с натуральным показателем.

Развивающие: - развитие математически грамотной речи, логического мышления,
сознательного восприятия учебного материала.

Воспитательные: – воспитание познавательной активности,
культуры общения, культуры диалога, интереса к математике.

Цели урока:Общеобразовательные: – знакомство со свойством возведения степени в степень, отработка умений систематизировать, обобщать знания о степени

Слайд 4Закончите фразу
1) Произведение n множителей, каждый из которых равен a ,

называется…

2) Степенью числа a с натуральным показателем 1 называется …

3) 137; 57; 0,27. Показателем степени служит число …

4) Вставьте знак неравества: а2 … 0, - а2 … 0

5) Частное степеней an : ak=an - k При делении степеней с ___________________________надо основание _______________,

а показатели степеней_____________________.

степень

число а

одинаковыми основаниями

оставить тем же

вычесть

Закончите фразу1) Произведение n множителей, каждый из которых равен a , называется… 2) Степенью числа a

Слайд 5«МОЗГОВОЙ ШТУРМ»
64
2
-2
-8
3
6
6
2
4
1
64

Слайд 6ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
(25)2
=25•25
=25+5

=210
(32)3
=32•32•32
=32+2+2

=36
(а n) m= a mn

При возведении степени

в степень показатели
перемножаются, а основание остаётся неизменным.

Докажем, что

ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА(25)2 =25•25=25+5=210(32)3 =32•32•32=32+2+2=36(а n) m= a mnПри возведении степени в степень показатели перемножаются, а основание

Слайд 7Представьте в виде степени
1) (32)5 =
2) (53)4=
3) (256)3=
4)

(m3)2 =

5) (а4)5=

6) (р6)7 =

7) (ax)y =

8) (вf)n=

310

512

2518

а20

р42

axy

вfn

Представьте в виде степени1) (32)5 = 2) (53)4= 3) (256)3= 4) (m3)2 = 5) (а4)5= 6) (р6)7

Слайд 8Си́мон Сте́вин (нидерл. Simon Stevin, 1548—1620) — фламандский математик-универсал, инженер.
Нидерландский математик

Симон Стевин в 16-17 веках предпринял первые шаги к построению современной теории степени. Он обозначал неизвестную величину кружком, а внутри его указывал показатели степени.

Запись 3(3)+5(2)–4 обозначала такую современную запись

33 + 52 – 4

Си́мон Сте́вин (нидерл. Simon Stevin, 1548—1620) — фламандский математик-универсал, инженер.Нидерландский математик Симон Стевин в 16-17 веках предпринял

Слайд 9Современная запись показателя степени введена Декартом в его «Геометрии» (1637), правда,

только для натуральных степеней, больших 2. Позднее Ньютон распространил эту форму записи на отрицательные и дробные показатели (1676), трактовку которых к этому времени уже предложил Стевин.

Мыслю, следовательно существую.
Рене Декарт

Французский философ и математик.

Современная запись показателя степени введена Декартом в его «Геометрии» (1637), правда, только для натуральных степеней, больших 2.

Слайд 101. Запишите в виде степени с основанием х
А)

(х3)2; Б) (х5)6 ; В) (х7)17

2) Представьте 240 в виде степени с основанием:
А) 28; Б) 210; В) 220

3) Вычислите значение выражения при
заданном значении х = -2
125 - х 4

1. Запишите в виде степени с основанием х А) (х3)2; Б) (х5)6 ;

Слайд 11Вариант 1.

Вариант 2.

ТЕСТ

Слайд 12Рефлексия

Слайд 13Домашнее задание
1.Выучить свойства степени с доказательством
2.Заполните свободные клетки квадрата так, чтобы

произведение выражений каждого столбца, каждой строки и диагонали равнялось

Такой квадрат называется магическим.

Домашнее задание1.Выучить свойства степени с доказательством2.Заполните свободные клетки квадрата так, чтобы произведение выражений каждого столбца, каждой строки

Слайд 14СПАСИБО ЗА УРОК!!!

Скачать презентацию

Презентация, доклад к уроку Свойства степени с натуральным показателем

Содержание

Слайд 1Свойства степени с
натуральным показателем

Слайд 2«Пусть кто-нибудь
попробует вычеркнуть
из математики степени,
и он увидит, что
без них далеко

Слайд 3Цели урока:
Общеобразовательные: – знакомство со свойством возведения степени в степень,
отработка

Слайд 4Закончите фразу
1) Произведение n множителей, каждый из которых равен a ,

Слайд 5«МОЗГОВОЙ ШТУРМ»
64
2
-2
-8
3
6
6
2
4
1
64

Слайд 6ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
(25)2
=25•25
=25+5

=210
(32)3
=32•32•32
=32+2+2

=36
(а n) m= a mn

При возведении степени

Слайд 7Представьте в виде степени
1) (32)5 =
2) (53)4=
3) (256)3=
4)

Слайд 8Си́мон Сте́вин (нидерл. Simon Stevin, 1548—1620) — фламандский математик-универсал, инженер.
Нидерландский математик

Слайд 9Современная запись показателя степени введена Декартом в его «Геометрии» (1637), правда,

Слайд 101. Запишите в виде степени с основанием х
А)

Слайд 11Вариант 1.

Слайд 12Рефлексия

Слайд 13Домашнее задание
1.Выучить свойства степени с доказательством
2.Заполните свободные клетки квадрата так, чтобы

Слайд 14СПАСИБО ЗА УРОК!!!

Что такое shareslide.ru?

Обратная связь

Презентация, доклад к уроку Свойства степени с натуральным показателем

Содержание

Слайд 1Свойства степени с натуральным показателем

Слайд 2«Пусть кто-нибудьпопробует вычеркнутьиз математики степени, и он увидит, чтобез них далеко

Слайд 3Цели урока:Общеобразовательные: – знакомство со свойством возведения степени в степень, отработка

Слайд 4Закончите фразу1) Произведение n множителей, каждый из которых равен a ,

Слайд 5«МОЗГОВОЙ ШТУРМ»642-2-836624164

Слайд 6ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА(25)2 =25•25=25+5=210(32)3 =32•32•32=32+2+2=36(а n) m= a mnПри возведении степени

Слайд 7Представьте в виде степени1) (32)5 = 2) (53)4= 3) (256)3= 4)

Слайд 8Си́мон Сте́вин (нидерл. Simon Stevin, 1548—1620) — фламандский математик-универсал, инженер.Нидерландский математик

Слайд 9Современная запись показателя степени введена Декартом в его «Геометрии» (1637), правда,

Слайд 101. Запишите в виде степени с основанием х А)

Слайд 11Вариант 1.

Слайд 12Рефлексия

Слайд 13Домашнее задание1.Выучить свойства степени с доказательством2.Заполните свободные клетки квадрата так, чтобы

Слайд 14СПАСИБО ЗА УРОК!!!

Похожие презентации

Что такое shareslide.ru?

Обратная связь

Слайд 1Свойства степени с
натуральным показателем

Слайд 2«Пусть кто-нибудь
попробует вычеркнуть
из математики степени,
и он увидит, что
без них далеко

Слайд 3Цели урока:
Общеобразовательные: – знакомство со свойством возведения степени в степень,
отработка

Слайд 4Закончите фразу
1) Произведение n множителей, каждый из которых равен a ,

Слайд 5«МОЗГОВОЙ ШТУРМ»
64
2
-2
-8
3
6
6
2
4
1
64

Слайд 6ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
(25)2
=25•25
=25+5

=210
(32)3
=32•32•32
=32+2+2

=36
(а n) m= a mn

При возведении степени

Слайд 7Представьте в виде степени
1) (32)5 =
2) (53)4=
3) (256)3=
4)

Слайд 8Си́мон Сте́вин (нидерл. Simon Stevin, 1548—1620) — фламандский математик-универсал, инженер.
Нидерландский математик

Слайд 101. Запишите в виде степени с основанием х
А)

Слайд 13Домашнее задание
1.Выучить свойства степени с доказательством
2.Заполните свободные клетки квадрата так, чтобы