- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по теории вероятности
Содержание
- 1. Презентация к уроку по теории вероятности
- 2. РЕШЕНИЕ КОМБИНАТОРНЫХ ЗАДАЧ
- 3. Цели:обучающая: закрепление знаний о теории соединений как
- 4. Что изучает комбинаторика?Комбинаторика – раздел математики, в
- 5. Классическое определение вероятностиСтохастическим называют опыт, если заранее
- 6. Классическое определение вероятностиРавновозможными называют события, если в
- 7. Классическое определение вероятностиНесовместимыми (несовместными) называют события, если
- 8. Классическое определение вероятностиПолной группой событий называется множество
- 9. Самый простой метод решения комбинаторных задач –
- 10. Для конечных множеств событий при нахождении m
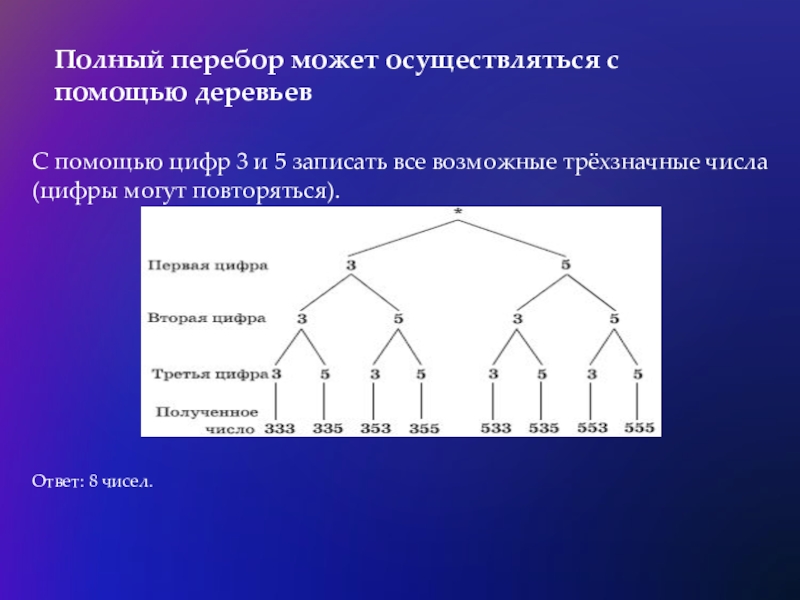
- 11. Полный перебор может осуществляться с помощью деревьевС
- 12. Полный перебор может осуществляться с помощью таблиц
- 13. Задача №2: Сколько пятизначных чисел можно
- 14. Вероятностью случайного события А называется отношение числа
- 15. Задачи открытого банка
- 16. В чемпионате по гимнастике участвуют 50 спортсменок:
- 17. № 1 В чемпионате по гимнастике участвуют
- 18. № 2В среднем из 1000 садовых насосов,
- 19. Благоприятное событие А: выбранный насос не подтекает.К-во
- 20. № 3Фабрика выпускает хрустальные изделия. В среднем
- 21. *Благоприятное событие А: купленное изделиеоказалось качественным.К-во благоприятных
- 22. ВероятностьДва события называются независимыми, если появление одного
- 23. Теорема о сложении вероятностейВероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.
- 24. № 4В кармане у Пети было 4
- 25. Вероятность и правило произведения Решение:Всего 6 монет.
- 26. № 5 В случайном эксперименте бросают три
- 27. № 5 В случайном эксперименте
- 28. № 6 В случайном эксперименте симметричную монету
- 29. * № 6 В случайном эксперименте
- 30. 1 вариант1. В случайном эксперименте бросают две
- 31. 1 вариант1. 0.22. 0.982 вариант1. 0.142. 0.99Ответы
- 32. Основные задачи комбинаторики составление упорядоченных множеств
- 33. Учимся различать виды соединений
- 34. ПерестановкиПерестановками из n элементов называются соединения,
- 35. РазмещенияРазмещениями из m элементов по n
- 36. РазмещенияЗадача 2. Сколькими способами могут занять I,
- 37. СочетанияСочетаниями из n элементов по
- 38. СочетанияЗадача 2. Сколькими способами можносоставить букет из
- 39. Проверь себя1. Сколькими способами 4 вора могут
- 40. 1. В случайном эксперименте бросают две
Слайд 1
«Путь размышлений - самый благородный,
путь
Конфуций
Слайд 3Цели:
обучающая: закрепление знаний о теории соединений как о самостоятельном разделе математики,
развивающая: развитие комбинаторного мышления и познавательного интереса;
воспитательная: овладение аппаратом решения вероятностных задач (умственное воспитание).
Слайд 4Что изучает комбинаторика?
Комбинаторика – раздел математики, в котором исследуются и решаются
Слайд 5Классическое определение вероятности
Стохастическим называют опыт, если заранее нельзя предугадать его результаты.
Пример: выбрасывается игральный кубик (опыт);
выпадает двойка (событие).
Событие, которое обязательно произойдет в результате испытания, называется достоверным, а которое не может произойти, - невозможным.
Пример: Выбрасываются две игральные кости.
Опыт – выбрасывание костей.
Достоверное событие – кости упадут.
Невозможное событие – выпадет 217 очков.
Слайд 6Классическое определение вероятности
Равновозможными называют события, если в результате опыта ни одно
Примеры: 1) Опыт - выбрасывается монета.
Выпадение орла и выпадение решки –
равновозможные события.
2) В урне лежат три шара. Два белых и синий.
Опыт – извлечение шара.
События – извлекли синий шар и извлекли
белый шар - неравно возможны.
Появление белого шара имеет больше шансов..
Слайд 7Классическое определение вероятности
Несовместимыми (несовместными) называют события, если наступление одного из них
Пример: 1) В результате одного выбрасывания выпадает
орел (событие А) или решка (событие В).
События А и В - несовместны.
2) В результате двух выбрасываний выпадает
орел (событие А) или решка (событие В).
События А и В - совместны. Выпадение орла в первый раз
не исключает выпадение решки во второй
Слайд 8Классическое определение вероятности
Полной группой событий называется множество всех событий рассматриваемого опыта,
Пример: 1) Опыт – один раз выбрасывается монета.
Элементарные события: выпадение орла
и выпадение решки образуют полную группу.
События образующие полную группу называют элементарными.
Слайд 9Самый простой метод решения комбинаторных задач – перебор всех возможных вариантов
Подсчитать
Ответ:11
Перечислить виды: 1)треугольников, 2)четырехугольников.
Ответ:1)равносторонний, равнобедренный, разносторонний; остроугольный, прямоугольный, тупоугольный.
2) параллелограмм, прямоугольник, ромб, квадрат, трапеция.
В магазине продают бейсболки трех цветов: синие, красные и черные. Ваня и Андрей покупают себе по одной. Сколько существует различных вариантов покупки?
Ответ:9 вариантов.
Слайд 10Для конечных множеств событий при нахождении m и n широко используют
Задача №1: Сколько двузначных чисел можно
составить, используя цифры 7; 8; 9
(цифры могут повторяться)?
В данном случае легко перебрать все комбинации.
77
78
79
88
87
89
99
97
98
9 вариантов
Слайд 11Полный перебор может осуществляться с помощью деревьев
С помощью цифр 3 и
Ответ: 8 чисел.
Слайд 12Полный перебор может осуществляться с помощью таблиц и графов
Встретились пятеро, каждый
Ответ:10.
С помощью таблицы вариантов
перечислить все возможные
двухбуквенные коды, в которых
используются буквы: x,y,z.
Ответ: 9.
Слайд 13Задача №2: Сколько пятизначных чисел можно
Как видим, в этой задаче перебор довольно затруднителен.
Решим задачу иначе.
На первом месте может стоять
любая из трех цифр – 3 варианта.
На втором месте может стоять
любая из трех цифр – 3 варианта.
На третьем месте может стоять
любая из трех цифр – 3 варианта.
На четвертом месте может стоять
любая из трех цифр – 3 варианта.
На пятом месте может стоять
любая из трех цифр – 3 варианта.
Комбинаторное правило умножения
Слайд 14Вероятностью случайного события А называется отношение числа элементарных событий, которые благоприятствуют
P(A) = m/n
Классическое определение вероятности
Слайд 16В чемпионате по гимнастике участвуют 50 спортсменок: 20 из США, 16
№ 1
Слайд 17№ 1 В чемпионате по гимнастике участвуют 50 спортсменок: 20 из США,
Благоприятное событие А: первой выступает
спортсменка из Канады
К-во благоприятных
событий: m=?
К-во всех событий группы: n=?
Соответствует количеству гимнасток из Канады.
m=50-(20+16)=14
Соответствует количеству всех гимнасток.
n=50
Слайд 18№ 2
В среднем из 1000 садовых насосов, поступивших в продажу, 10
Слайд 19
Благоприятное событие А: выбранный насос не подтекает.
К-во благоприятных
событий: m=?
К-во всех
Соответствует количеству исправных насосов
m=1000-10=990
Соответствует количеству всех насосов.
n=1000
№ 2
В среднем из 1000 садовых насосов, поступивших в продажу, 10 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Слайд 20№ 3
Фабрика выпускает хрустальные изделия.
В среднем на 190 качественных изделий
Результат округлите до сотых.
Слайд 21*
Благоприятное событие А: купленное изделие
оказалось качественным.
К-во благоприятных
событий: m=?
К-во всех событий
Соответствует количеству качественных изделий.
m=190
Соответствует количеству всех изделий.
n=190+8=198
№ 3
Фабрика выпускает хрустальные изделия.
В среднем на 190 качественных изделий приходится восемь со скрытыми дефектами. Найдите вероятность того, что купленное изделие окажется качественным.
Результат округлите до сотых.
Слайд 22Вероятность
Два события называются независимыми, если появление одного из них не влияет
Теорема об умножении вероятностей
Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.
Слайд 23Теорема о сложении вероятностей
Вероятность появления одного из двух несовместных событий равна
Слайд 24№ 4
В кармане у Пети было 4 монеты по рублю и
Петя, не глядя, переложил какие-то три монеты в другой карман.
Найдите вероятность того, что пятирублевые монеты лежат в разных карманах.
Слайд 25Вероятность и правило произведения
Решение:
Всего 6 монет. Возможны варианты перекладывания:
1 карман
5 1 1 5 1 1
1 5 1 1 5 1
1 1 5 1 1 5
P1 = 2/6 * 4/5 * 3/4 = 1/5
«5» «1» «1»
P2 =4/6 * 2/5 * 3/4 = 1/5
«1» «5» «1»
P3 =4/6 * 3/5 * 2/4 = 1/5
«1» «1» «5»
P = P1 + P2 + P3 = 3/5 = 0,6
№ 4
В кармане у Пети было 4 монеты по рублю и 2 монеты по 5 рублей.
Петя, не глядя, переложил какие-то три монеты в другой карман.
Найдите вероятность того, что пятирублевые монеты лежат в
разных карманах.
Слайд 26№ 5 В случайном эксперименте бросают три игральные кости. Найдите вероятность того,
Слайд 27 № 5 В случайном эксперименте бросают три игральные кости. Найдите вероятность того,
*
Благоприятное событие А: в сумме выпало 7 очков.
К-во благоприятных
событий m=?
115
124
133
142
151
214
223
232
241
313
322
331
К-во всех событий группы n=?
1-я кость - 6 вариантов
2-я кость - 6 вариантов
3-я кость - 6 вариантов
412 421
511
Слайд 28№ 6 В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того,
Слайд 29*
№ 6
В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того,
Условие можно трактовать так: какова вероятность того,
что все четыре раза выпадет решка?
К-во благоприятных
событий m=?
К-во всех событий группы n=?
m=1
Четыре раза выпала
решка.
1-й раз - 2 варианта
2-й раз - 2 варианта
3-й раз - 2 варианта
4-й раз - 2 варианта
Слайд 301 вариант
1. В случайном эксперименте бросают две игральные кости. Найдите вероятность
2. В среднем из 150 садовых насосов, поступивших в продажу, 3 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
2 вариант
1. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 6 очков. Результат округлите до сотых
2.В среднем из 1300 садовых насосов, поступивших в продажу, 13 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Самостоятельная работа
Слайд 32Основные задачи комбинаторики
составление упорядоченных множеств (образование перестановок);
составление упорядоченных подмножеств данного множества (образование размещений).
Чтобы отличать задачи на подсчёт числа размещений от задач на подсчёт числа сочетаний, определим, важен или нет порядок в следующих выборках:
а) судья хоккейного матча и его помощник;
б) три ноты в аккорде;
в) «Шесть человек останутся убирать класс!»
г) две серии для просмотра из многосерийного фильма.
Ответ: а)да; б)нет; в)нет; г)да.
Слайд 34Перестановки
Перестановками из n элементов называются соединения, которые состоят из
Permutation (фр.) – перестановка.
Задача. Сколькими способами можно расположить в столбик три детали конструктора, различающиеся по цвету?
Ответ:6.
Слайд 35Размещения
Размещениями из m элементов по n элементов
(
данных разных элементов, и которые отличаются одно от другого либо самими элементами, либо порядком их расположения.
Задача 1. Сколькими способами можно изготовить трёхцветный флаг с горизонтальными полосами, если имеется материал 7 различных цветов?
Ответ: 210.
Слайд 36Размещения
Задача 2.
Сколькими способами могут
занять I, II, III места
8 участниц финального забега
на дистанции 100 м?
Ответ: 366.
Задача 3.
Из 30 участников собрания надо выбрать председателя и секретаря. Сколькими способами это можно сделать?
Ответ: 870.
Слайд 37Сочетания
Сочетаниями из n элементов по m элементов
Задача 1. В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?
Ответ: 21.
Слайд 38Сочетания
Задача 2.
Сколькими способами можно
составить букет из трёх роз, выбирая
цветы из
Ответ: 84.
Задача 3.
В классе учатся 16 мальчиков и 12 девочек. Сколькими способами можно выделить 4 мальчиков и 3 девочек для уборки территории?
Ответ:
Слайд 39Проверь себя
1. Сколькими способами 4 вора могут разбежаться на 4 разные
2. Из колоды в 36 карт выбирают 5 карт и одновременно открывают их. Найдите число всех возможных вариантов выбранных карт.
3. Сколькими способами из класса, где учатся 24 ученика, можно выбрать: а)двух дежурных; б)старосту и помощника старосты?
Ответ: а)276; б)552.
4. «Проказница Мартышка, Осёл, Козёл да косолапый Мишка задумали сыграть квартет». Сколькими способами они могут выбрать каждый для себя по одному инструменту из 10 данных различных инструментов?
Ответ:
Слайд 40 1. В случайном эксперименте бросают две игральные кости. Найти вероятность
2. Составить и решить 3 задачи по данной теме.
Домашнее задание