средняя школа №2»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по теме Возрастание и убывание функций
Содержание
- 1. Презентация к уроку по теме Возрастание и убывание функций
- 2. Цель урока:ввести признаки возрастания и убывания функции,
- 3. Укажите промежутки возрастания (убывания) функции:у = х²
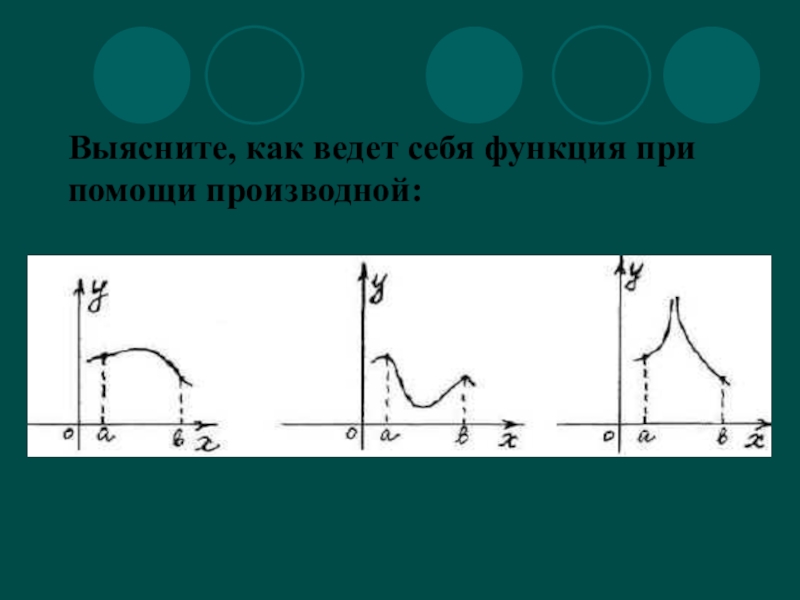
- 4. Выясните, как ведет себя функция при помощи производной:
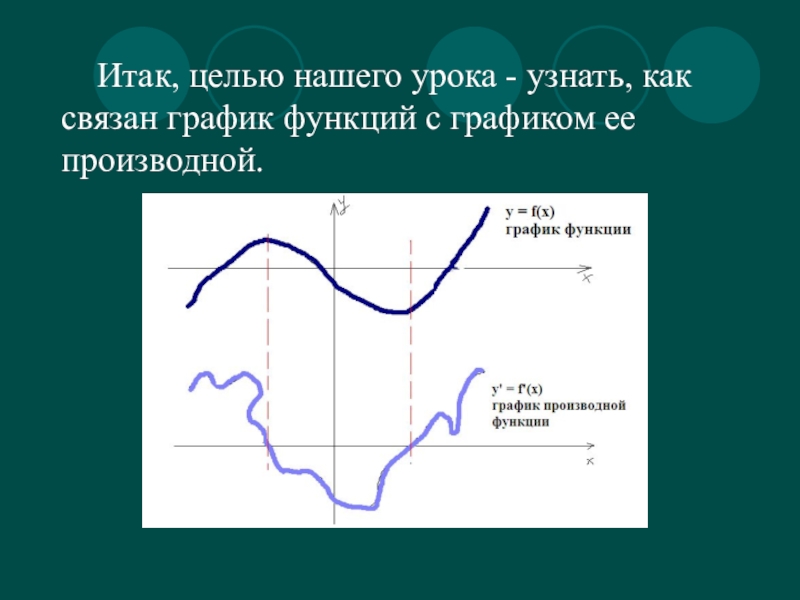
- 5. Итак, целью нашего урока - узнать, как связан график функций с графиком ее производной.
- 6. Достаточный признак возрастания(убывания) функции y = f(х)
- 7. План исследования функции на возрастание (убывание):Найти область
- 8. Пример: у = 0,6х – 4х³ + 7 5
- 9. Решение:Определена при любом х. у ' =
- 10. Дьёрдь Пойа, Джордж Полиа (1887-1985) — венгерский,
- 11. Пример № 2: у = х³– 3х²;
- 12. Проверка
- 13. Пример №3: у = х³ — 6
- 14. В развитии дифференциального и интегрального исчисления главная
- 15. Ньютон был самоучкой в математике. Став студентом
- 16. В мае того же года он открыл
- 17. Производная – одно из фундаментальных понятий математики.
- 18. Независимо друг от друга И.
- 19. Большую роль в развитии дифференциального исчисления сыграл
- 20. Творческое задание Отыщите функцию в таблице, исходя из
- 21. Я – функция сложная, это известно, Ещё
- 22. Таблица Будь внимателен!
Цель урока:ввести признаки возрастания и убывания функции, научиться применять их при решении задач;развивать познавательную деятельность, интерес к предмету, точность и логичность мышления;воспитывать ответственность, самостоятельность.
Слайд 1Возрастание и убывание функций
Презентацию подготовила
учитель математики I категории
Коржова Вера Валерьевна
МБОУ «Советская
Слайд 2Цель урока:
ввести признаки возрастания и убывания функции, научиться применять их
при решении задач;
развивать познавательную деятельность, интерес к предмету, точность и логичность мышления;
воспитывать ответственность, самостоятельность.
развивать познавательную деятельность, интерес к предмету, точность и логичность мышления;
воспитывать ответственность, самостоятельность.
Слайд 3Укажите промежутки возрастания (убывания) функции:
у = х² – 2;
у = 3/х
у=
-х² - 3х +4
у = 0,6x – 4х³ + 7
у = 0,6x – 4х³ + 7
5
Слайд 6Достаточный признак возрастания(убывания) функции y = f(х) :
Если функция f(х)
дифференцируема на интервале (a;b) и f '(x) > 0 для всех хϵ(a;b), то функция возрастает на интервале (a;b).
Если функция f(х) дифференцируема на интервале (a;b) и f '(x) < 0 для всех хϵ(a;b), то функция убывает на интервале (a;b).
Если функция f(х) дифференцируема на интервале (a;b) и f '(x) < 0 для всех хϵ(a;b), то функция убывает на интервале (a;b).
Слайд 7План исследования функции на возрастание (убывание):
Найти область определения;
Найти производную функции;
Найти точки,
в которых производная равна нулю или не существует, т.е. критические точки;
Определить знаки производной в промежутках, на которых найденные критические точки делят область определения функции;
Вывод о «поведении» функции, применив признаки.
Определить знаки производной в промежутках, на которых найденные критические точки делят область определения функции;
Вывод о «поведении» функции, применив признаки.
Слайд 9Решение:
Определена при любом х.
у ' = 3x – 12х²
у '
существует во всех точках. у ' = 0; 3x – 12х² = 0; 3х² (х – 2)(х + 2) = 0
у ' + – – +
y -2 0 2
Функция возрастает при хϵ (–∞; –2] U[2; +∞). Функция убывает при хϵ [–2; +2].
у ' + – – +
y -2 0 2
Функция возрастает при хϵ (–∞; –2] U[2; +∞). Функция убывает при хϵ [–2; +2].
4
4
Слайд 10Дьёрдь Пойа, Джордж Полиа (1887-1985) — венгерский, швейцарский и американский математик.
«Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.»
Слайд 13Пример №3: у = х³ — 6 х² + 9 х
— 9;
Пример №4:у = 3 х² — 5х + 4;
Пример №5: у = 2 х³ – 3 х² – 36 х + 40;
Пример №6 : у = х4 - 2 х³
Я ВЕРЮ В ТЕБЯ!
Слайд 14 В развитии дифференциального и интегрального исчисления главная роль принадлежала двум великим
ученым – англичанину Исааку Ньютону(1643-1727) и немцу Готфриду Вильгельму Лейбницу (1646-1716).
Слайд 15 Ньютон был самоучкой в математике. Став студентом Кембриджского университета, впервые пришел
на экзамен по математике, выяснилось, что Исаак прочел множество математических книг и уже почувствовал вкус к математическим проблемам.
Во время эпидемии чумы университет закрылся и Ньютон почти 2 года провел в своем пометье Вулсторп в графстве Линкольншир.
Во время эпидемии чумы университет закрылся и Ньютон почти 2 года провел в своем пометье Вулсторп в графстве Линкольншир.
Слайд 16 В мае того же года он открыл биом Ньютона, метод касательных,
а в ноябре – прямой метод флюксий.
Функции Ньютон называл флюентами, т.е. «текущими» (отлат. flue – «теку»), а (цитата) «скорости, с которыми каждая флюента увеличивается в силу порождающего движения» - флюксиями (мы их называем производными). Они обозначались теми же буквами, но с точкой вверху: ẋ, ẏ.
Функции Ньютон называл флюентами, т.е. «текущими» (отлат. flue – «теку»), а (цитата) «скорости, с которыми каждая флюента увеличивается в силу порождающего движения» - флюксиями (мы их называем производными). Они обозначались теми же буквами, но с точкой вверху: ẋ, ẏ.
«Метод флюксий и бесконечных рядов» Лондон 1736г.
Слайд 17Производная – одно из фундаментальных понятий математики. Оно возникло в XVII
веке в связи с необходимостью решения ряда задач из физики, механики и математики, но в первую очередь следующих двух: определение скорости прямолинейного движения и построения касательной к прямой.
Слайд 18 Независимо друг от друга И. Ньютон и Г. Лейбниц
разработали аппарат, которым мы и пользуемся в настоящее время. И. Ньютон в основном опирался на физическое представление о мгновенной скорости движения, а Г. Лейбниц использовал понятие бесконечно малой.
Исчисление, созданное Ньютоном и Лейбницем, получило название дифференциального исчисления. С его помощью был решен целый ряд задач теоретической механики, физики и астрономии.
Слайд 19Большую роль в развитии дифференциального исчисления сыграл Л. Эйлер, написавший учебник
“Дифференциальное исчисление”.
Используя методы дифференциального исчисления, ученые предсказали возвращение кометы Галлея, что было большим триумфом науки XVII века.
В настоящее время понятие производной находит большое применение в различных областях науки и техники.
Используя методы дифференциального исчисления, ученые предсказали возвращение кометы Галлея, что было большим триумфом науки XVII века.
В настоящее время понятие производной находит большое применение в различных областях науки и техники.
Слайд 20Творческое задание
Отыщите функцию в таблице, исходя из её «автобиографии». Найдите область
определения, корень, точку разрыва, промежуток возрастания и убывания.
Слайд 21 Я – функция сложная, это известно, Ещё расскажу, если вам интересно, Что точку
разрыва и корень имею,
И есть интервал, где расти не посмею.
Во всём остальном положительна, право,
И это, конечно, не ради забавы.
Для чисел больших я стремлюсь к единице.
Найдите меня среди прочих в таблице.