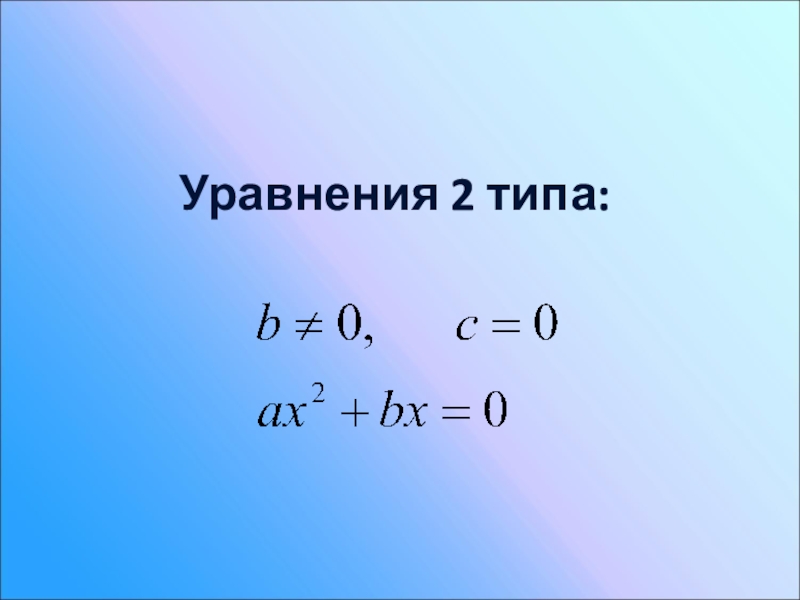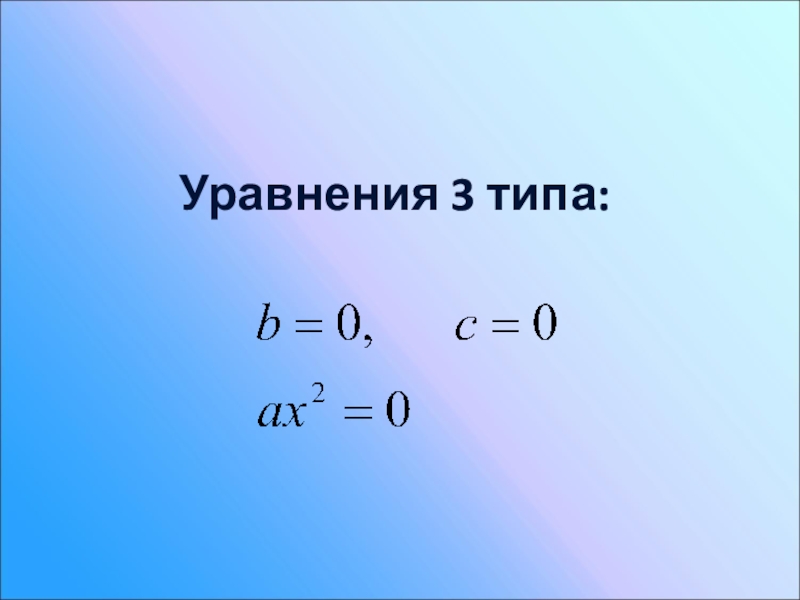- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по теме Неполные квадратные уравнения
Содержание
- 1. Презентация к уроку по теме Неполные квадратные уравнения
- 2. Цели урока: Познакомить учащихся с общим видом
- 3. Вопросы:Что такое уравнение?Что значит «решить уравнение»?Что называется корнем уравнения?А как вы думаете, когда появились квадратные уравнения?
- 4. Историческая справка.Квадратные уравнения умели решать около 2000
- 5. Задача знаменитого индийского математика Бхаскары:Обезьянок резвых стаяВсласть
- 6. Уравнение к задаче Бхаскары:
- 7. Задача по геометрии, приводящая к квадратному уравнению:Дан
- 8. Решение:Пусть х – длина катета.По теореме Пифагора:BCA
- 9. Задача по физике, приводящая к квадратному уравнению:Дан
- 10. Решение:Масса тела равна:Объем прямоугольного параллелепипеда равен:
- 11. Определение квадратного уравнения:Уравнение вида
- 12. Выберите из уравнений квадратные
- 13. Определение неполного квадратного уравнения:Те квадратные уравнения, в
- 14. Уравнения 1 типа:
- 15. Решение уравнения 1 типа:Если и
- 16. Уравнения 2 типа:
- 17. Решение уравнения 2 типа:Уравнение имеет два корня, один из которых равен нулю.
- 18. Уравнения 3 типа:
- 19. Решение уравнения 3 типа:Это уравнение имеет единственный корень
- 20. Устные упражнения:
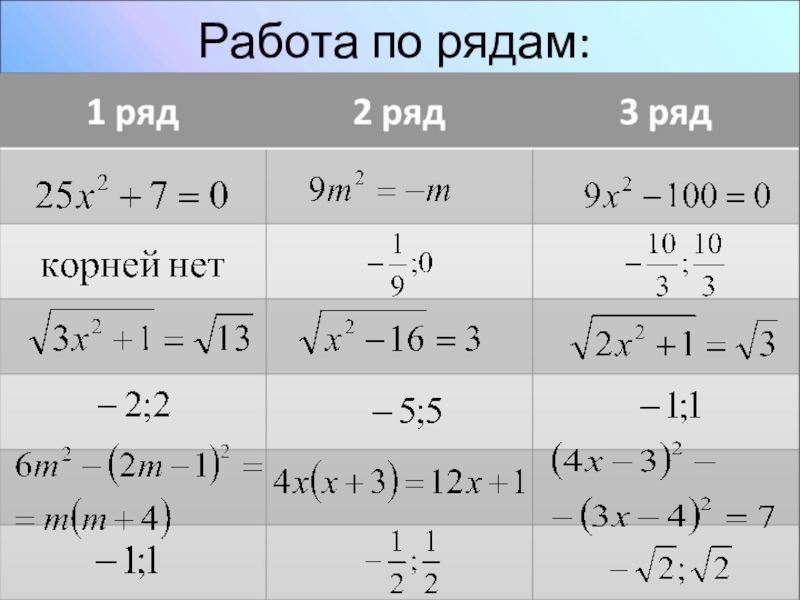
- 21. Работа по рядам:
- 22. Уравнение с параметром:При каких значениях m ровно
- 23. Решение:Уравнение
- 24. Для данного уравнения составим следующую систему и
- 25. Домашнее задание:Мордкович п. 24 учить № 24.16-24.22 (а,б), 24.30
Цели урока: Познакомить учащихся с общим видом квадратного уравнения, понятием неполного квадратного уравнения и способами их решения, показать, что источником возникновения квадратных уравнений является реальный мир, что эти уравнения возникли из практических потребностей людей
Слайд 1Учитель математики: Тимофеева Марина Николаевна
Саратов, 2018-2019
Определение квадратного уравнения.
Неполные квадратные уравнения.
Слайд 2Цели урока:
Познакомить учащихся с общим видом квадратного уравнения, понятием неполного
квадратного уравнения и способами их решения, показать, что источником возникновения квадратных уравнений является реальный мир, что эти уравнения возникли из практических потребностей людей
Слайд 3Вопросы:
Что такое уравнение?
Что значит «решить уравнение»?
Что называется корнем уравнения?
А как вы
думаете, когда появились квадратные уравнения?
Слайд 4Историческая справка.
Квадратные уравнения умели решать около 2000 лет до нашей эры
вавилоняне.
В Древней Индии уже в 499 году были распространены публичные соревнования в решении трудных задач на составление квадратных уравнений.
В Древней Индии уже в 499 году были распространены публичные соревнования в решении трудных задач на составление квадратных уравнений.
Слайд 5Задача знаменитого индийского математика Бхаскары:
Обезьянок резвых стая
Всласть поевши, развлекаясь,
Их в квадрате
часть восьмая
На поляне забавлялась.
А двенадцать по лианам
Стали прыгать, повисая.
Сколько было обезьянок
Ты скажи мне в этой стае?
На поляне забавлялась.
А двенадцать по лианам
Стали прыгать, повисая.
Сколько было обезьянок
Ты скажи мне в этой стае?
Слайд 7Задача по геометрии, приводящая к квадратному уравнению:
Дан прямоугольный равнобедренный треугольник, у
которого длина гипотенузы равна 50. Чему равна длина катета?
B
C
A
Слайд 9Задача по физике, приводящая к квадратному уравнению:
Дан слиток серебра формы прямоугольного
параллелепипеда, в основании которого квадрат. Масса слитка – m, ρ – плотность, h – высота. Найти сторону основания.
Слайд 10
Решение:
Масса тела равна:
Объем прямоугольного параллелепипеда равен:
, где a,b,c – длины ребер.
Пусть , тогда .
Составим уравнение:
Пусть , тогда .
Составим уравнение:
Слайд 11Определение квадратного уравнения:
Уравнение вида
,
где - некоторые числа,
x- переменная, называется квадратным уравнением или уравнением второй степени.
где - некоторые числа,
x- переменная, называется квадратным уравнением или уравнением второй степени.
Слайд 13Определение неполного квадратного уравнения:
Те квадратные уравнения, в которых коэффициенты
или равны нулю, называются неполными квадратными уравнениями.
Слайд 15Решение уравнения 1 типа:
Если и одного знака,
то уравнение действительных корней не имеет.
Если и разного знака, то уравнение имеет два корня, которые равны по модулю, но противоположны по знаку:
Если и разного знака, то уравнение имеет два корня, которые равны по модулю, но противоположны по знаку:
Слайд 23Решение:
Уравнение
будет иметь ровно один корень, равный нулю, если выполняются следующие условия: