В кают-компании
5. Каюта капитана
6. Финиш
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по математике Исследование функций с помощью производной
Содержание
- 1. Презентация к уроку по математике Исследование функций с помощью производной
- 2. Критерии оценки25 и более баллов – «5»20-24
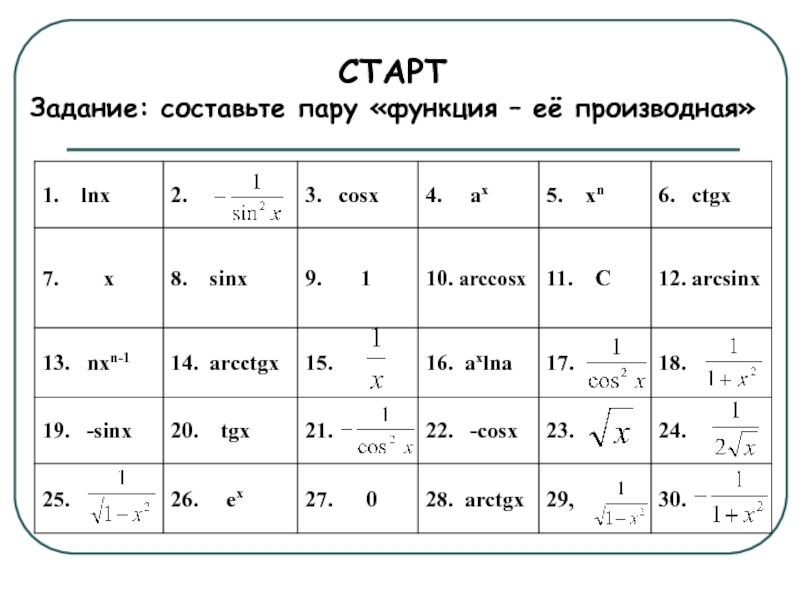
- 3. СТАРТЗадание: составьте пару «функция – её производная»
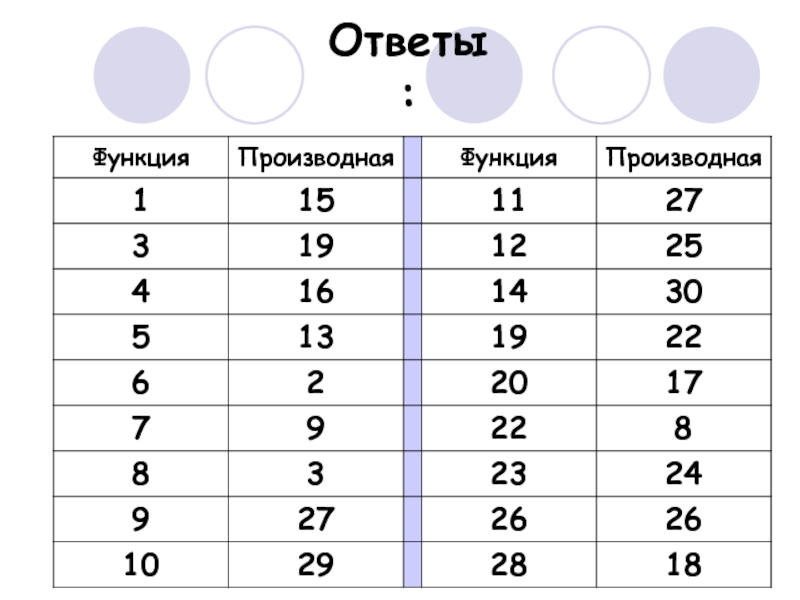
- 4. Ответы:
- 5. ШТОРМ1. На промежутке (0;2) y'(x) > 0,
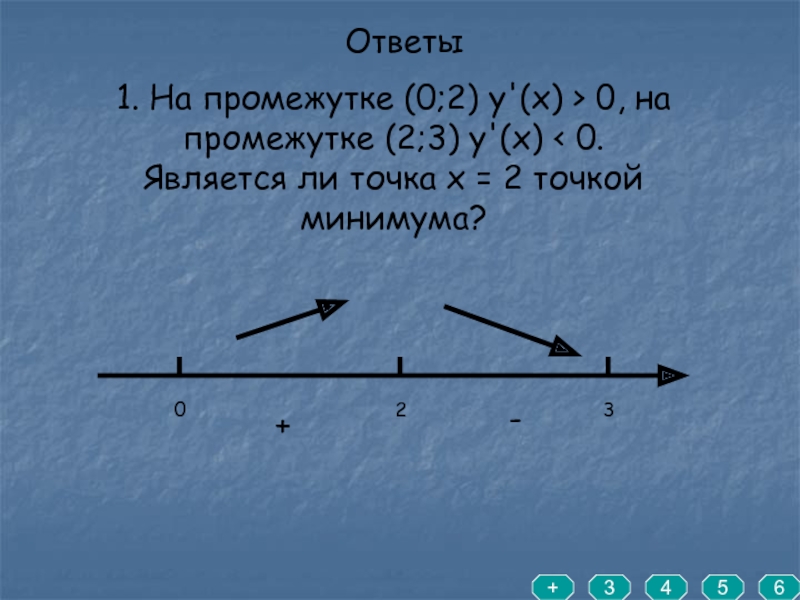
- 6. Ответы1. На промежутке (0;2) y'(x) > 0,
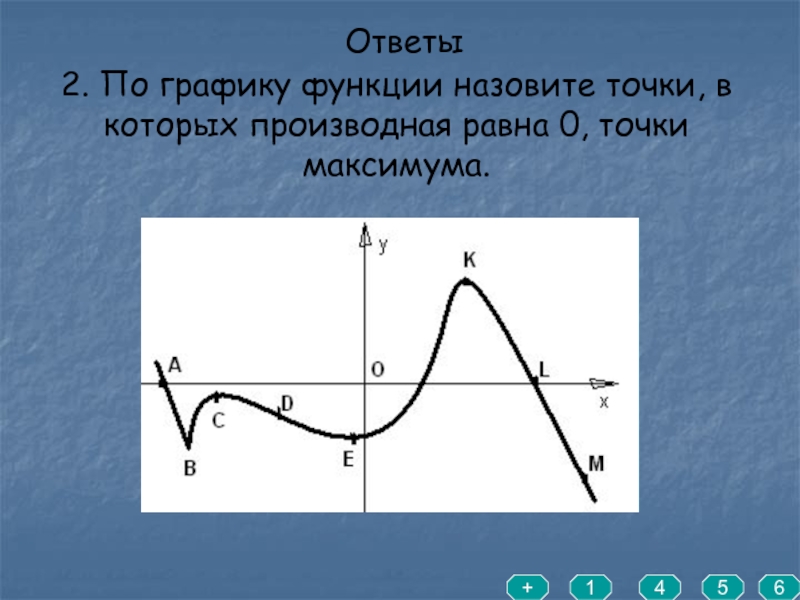
- 7. 2. По графику функции назовите точки, в которых производная равна 0, точки максимума. Ответы1+456
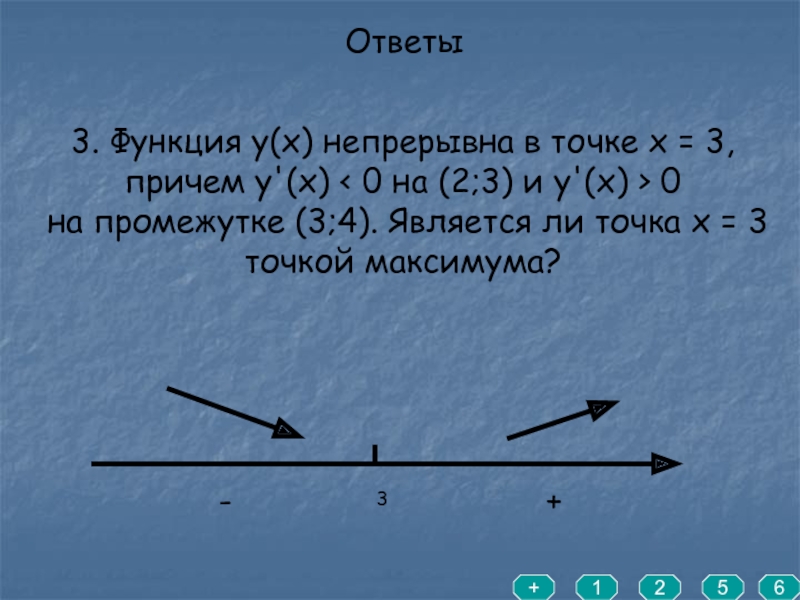
- 8. Ответы3. Функция y(x) непрерывна в точке х
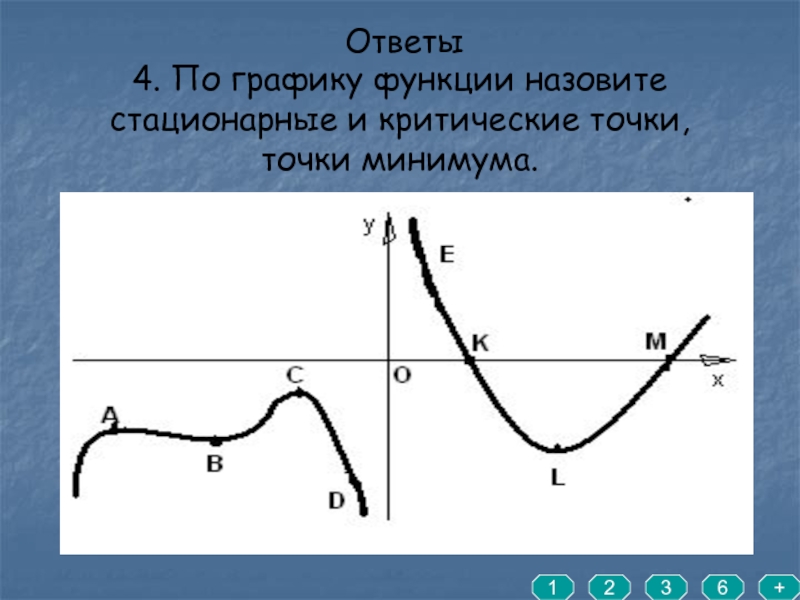
- 9. 4. По графику функции назовите стационарные и критические точки, точки минимума. Ответы123+6
- 10. 5. Является ли точка х = 2 критической для функции y(x), если D(y) = [-3;2]? Ответы1234+
- 11. 6. Функция непрерывна на отрезке [1;6]. В какой точке функция имеет наибольшее значение, если f’(x)
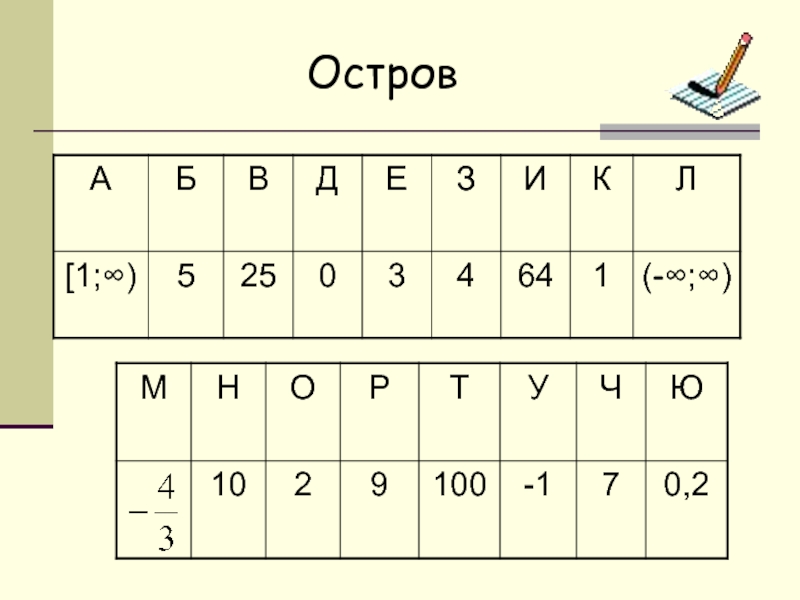
- 12. Остров
- 13. Образование - клад,труд – ключ к нему.П. Буаст
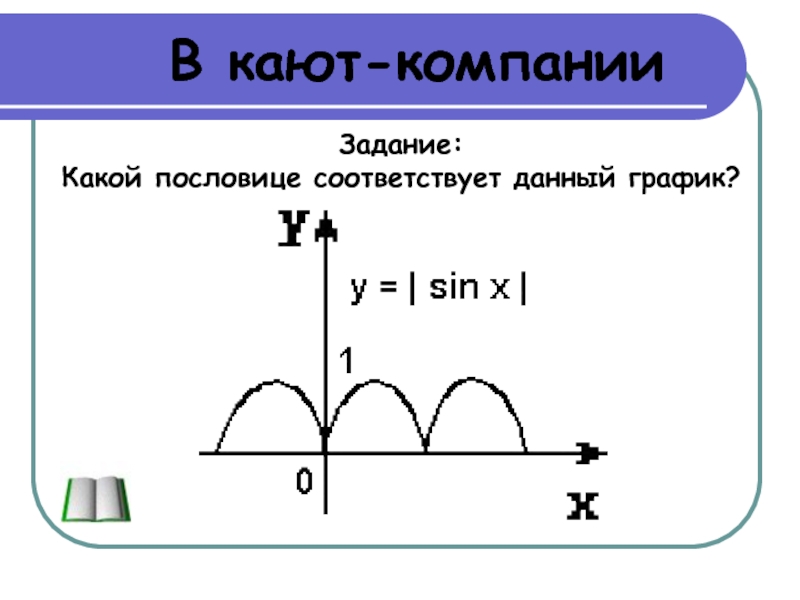
- 14. В кают-компанииЗадание: Какой пословице соответствует данный график?
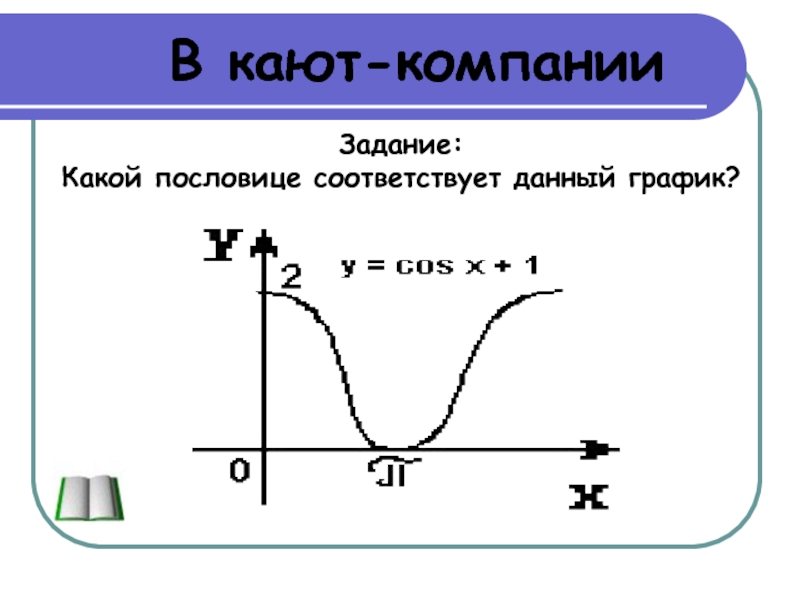
- 15. В кают-компанииЗадание: Какой пословице соответствует данный график?
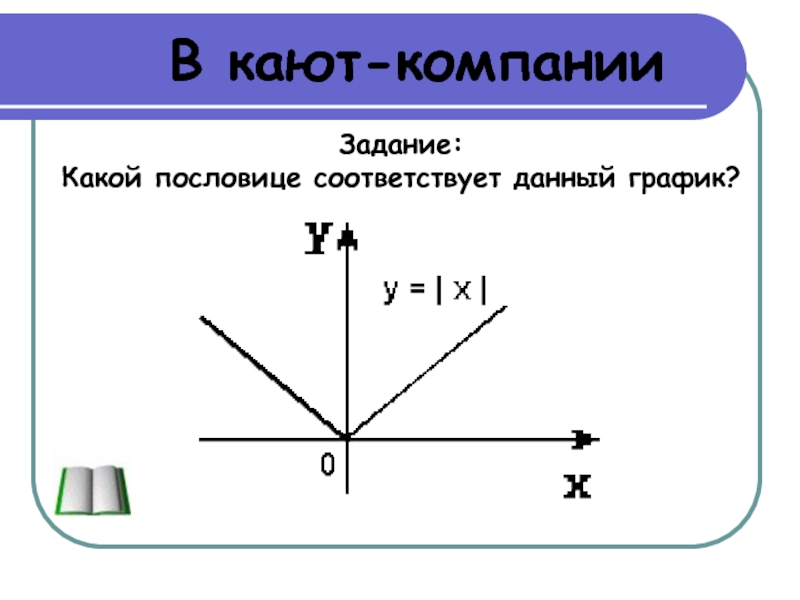
- 16. В кают-компанииЗадание: Какой пословице соответствует данный график?
- 17. Каюта капитанаЗавершите фразы: «Если на D(f) производная …, то функция у….»
- 18. Каюта капитанаОтветХХХХХ
- 19. ФинишЗадание 1:Определяя точки минимума функции, учащийся нашел,
- 20. ФинишЗадание 2:Определяя точки минимума функции, учащийся нашел
- 21. ФинишЗадание 3:График производной. Определяя точки минимума, ученик указал точку х = 2. Прав ли он?
- 22. ФинишЗадание 4:График производной. Определяя точки минимума, ученик
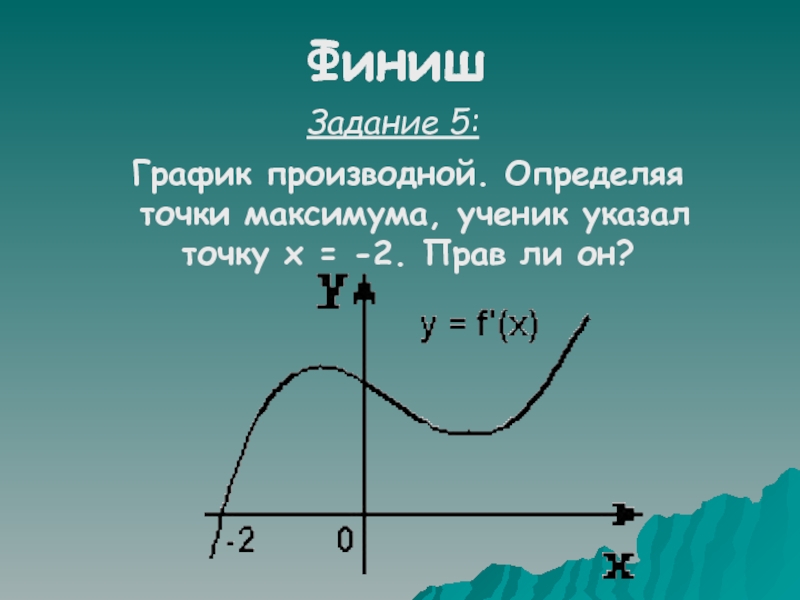
- 23. ФинишЗадание 5:График производной. Определяя точки максимума, ученик указал точку х = -2. Прав ли он?
- 24. Критерии оценки25 и более баллов – «5»20-24
- 25. Домашнее задание:Составить и оформить карточку, на которой:
- 26. Образование создает разницу между людьми.Дж. Локк
Критерии оценки25 и более баллов – «5»20-24 балла – «4»12-19 баллов – «3»Менее 12 баллов – «2»
Слайд 1Урок-путешествие по теме «Применение производной к исследованию функций»
План:
1. Старт
2. Шторм
3. Остров
4.
Слайд 2Критерии оценки
25 и более баллов – «5»
20-24 балла – «4»
12-19 баллов
– «3»
Менее 12 баллов – «2»
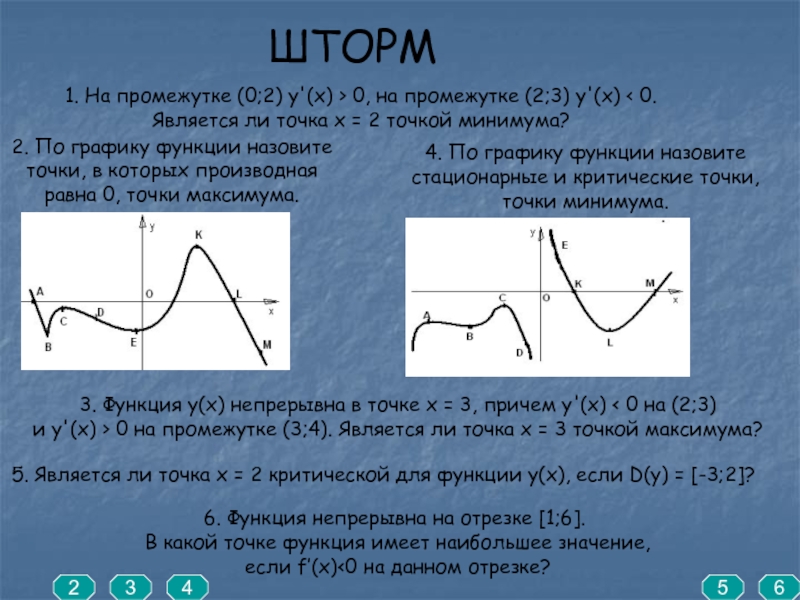
Слайд 5ШТОРМ
1. На промежутке (0;2) y'(x) > 0, на промежутке (2;3) y'(x)
< 0.
Является ли точка х = 2 точкой минимума?
Является ли точка х = 2 точкой минимума?
3. Функция y(x) непрерывна в точке х = 3, причем y'(x) < 0 на (2;3)
и y'(x) > 0 на промежутке (3;4). Является ли точка х = 3 точкой максимума?
5. Является ли точка х = 2 критической для функции y(x), если D(y) = [-3;2]?
2. По графику функции назовите
точки, в которых производная
равна 0, точки максимума.
6. Функция непрерывна на отрезке [1;6].
В какой точке функция имеет наибольшее значение,
если f’(x)<0 на данном отрезке?
4. По графику функции назовите
стационарные и критические точки,
точки минимума.
2
3
4
5
6
Слайд 6Ответы
1. На промежутке (0;2) y'(x) > 0, на промежутке (2;3) y'(x)
< 0.
Является ли точка х = 2 точкой минимума?
Является ли точка х = 2 точкой минимума?
0
3
2
+
-
+
3
4
5
6
Слайд 72. По графику функции назовите точки, в которых производная равна 0,
точки максимума.
Ответы
1
+
4
5
6
Слайд 8Ответы
3. Функция y(x) непрерывна в точке х = 3, причем y'(x)
< 0 на (2;3) и y'(x) > 0
на промежутке (3;4). Является ли точка х = 3 точкой максимума?
на промежутке (3;4). Является ли точка х = 3 точкой максимума?
3
+
-
1
2
+
5
6
![5. Является ли точка х = 2 критической для функции y(x), если D(y) = [-3;2]? Ответы1234+](/img/thumbs/2c68902355c78ed1b2873c8a275df466-800x.jpg "Презентация к уроку по математике Исследование функций с помощью производной 5. Является ли точка х = 2 критической для функции y(x), если D(y) = [-3;2]? Ответы1234+")
Слайд 116. Функция непрерывна на отрезке [1;6].
В какой точке функция имеет
наибольшее значение,
если f’(x)<0 на данном отрезке?
Ответы
х
у
0
У=f(x)
1 6
1
2
3
4
5
![6. Функция непрерывна на отрезке [1;6]. В какой точке функция имеет наибольшее значение, если f’(x)](/img/thumbs/a993631a4e826fb4fbfb688d951d8e1e-800x.jpg "Презентация к уроку по математике Исследование функций с помощью производной 6. Функция непрерывна на отрезке [1;6]. В какой точке функция имеет наибольшее значение, если f’(x)")
Слайд 19Финиш
Задание 1:
Определяя точки минимума функции,
учащийся нашел, при каких значениях
аргумента
значения функции равны 0.
Затем из этих значений он выбрал те,
проходя через которые функция меняет
знак с "-" на "+". Эти точки он назвал
точками минимума. Прав ли он?
Затем из этих значений он выбрал те,
проходя через которые функция меняет
знак с "-" на "+". Эти точки он назвал
точками минимума. Прав ли он?
Слайд 20Финиш
Задание 2:
Определяя точки минимума функции,
учащийся нашел те значения аргумента,
при
которых производная обращается в 0.
Эти точки он назвал точками минимума.
Прав ли он?
Эти точки он назвал точками минимума.
Прав ли он?
Слайд 21Финиш
Задание 3:
График производной.
Определяя точки минимума,
ученик указал точку х =
2. Прав ли он?
Слайд 22Финиш
Задание 4:
График производной. Определяя
точки минимума, ученик указал
точки х =
-4, х =1, х = 3. Прав ли он?
Слайд 23Финиш
Задание 5:
График производной. Определяя
точки максимума, ученик указал
точку х =
-2. Прав ли он?
Слайд 24Критерии оценки
25 и более баллов – «5»
20-24 балла – «4»
12-19 баллов
– «3»
Менее 12 баллов – «2»
Слайд 25Домашнее задание:
Составить и оформить карточку,
на которой: график
произвольной функции,
задания
на чтение
данного графика.
Ответы сдать на отдельном листе.
данного графика.
Ответы сдать на отдельном листе.
