- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по алгебре на тему: Формулы сложения (10 класс)
Содержание
- 1. Презентация к уроку по алгебре на тему: Формулы сложения (10 класс)
- 2. Устная работа.Какие знаки имеет синус, косинус, тангенс
- 3. Устная работа.а) Назовите формулу, выражающую связь между
- 4. Устная работа.
- 5. Устная работа.Вычислить: а) cos
- 6. Тема урокаФормулы сложения
- 7. Цель урокавывести формулы сложения для косинуса суммы
- 8. Расстояние между двумя точками с заданными координатами:Если
- 9. M1 (cos α; sin α)M2 (cos(-α); sin(-α))
- 10. Теорема Для любых α и β
- 11. ТеоремаИмеем: M0 (1; 0)
- 12. Запомните!cos(α + β) = cosα cosβ –
- 13. Закрепление изученных формул.№ 100-106 (нечетные)
- 14. 7. Итоги урокаИтак, сегодня на уроке мы
- 15. Домашнее заданиеПар. 8 стр. 282-284, выучить формулы№102-106 (четные), 108
Устная работа.Какие знаки имеет синус, косинус, тангенс и котангенс в каждой из координатных четвертей?Чему равен sin (- α) = cos (- α) =
Слайд 2Устная работа.
Какие знаки имеет синус, косинус, тангенс и котангенс в каждой
из координатных четвертей?
Чему равен sin (- α) =
cos (- α) =
tg (- α) =
Чему равен sin (- 45) = sin (- π) =
cos (- 45) = cos (- ) =
tg (- 45) = tg (- 2π ) =
Чему равен sin (- α) =
cos (- α) =
tg (- α) =
Чему равен sin (- 45) = sin (- π) =
cos (- 45) = cos (- ) =
tg (- 45) = tg (- 2π ) =
Слайд 3Устная работа.
а) Назовите формулу, выражающую связь между синусом и косинусом одного
и того же угла.
б) Чему равно выражение
в) Как выражается тангенс угла через косинус того же угла?
г) Как выражается котангенс угла через синус того же угла?
б) Чему равно выражение
в) Как выражается тангенс угла через косинус того же угла?
г) Как выражается котангенс угла через синус того же угла?
Слайд 5Устная работа.
Вычислить:
а) cos
б) sin в)cos(-45)
г) sin(-30) д) cosπ +sinπ
е) sin2 (5α+β) + cos2 (5α+β)
ж) cos75°; з) cos15°.
г) sin(-30) д) cosπ +sinπ
е) sin2 (5α+β) + cos2 (5α+β)
ж) cos75°; з) cos15°.
Слайд 7Цель урока
вывести формулы сложения для косинуса суммы и разности углов, отработать
их применение при вычислениях и выполнении преобразований тригонометрических выражений
Слайд 8Расстояние между двумя точками с заданными координатами:
Если А(х1;у1) и В(х2;у2), то
АВ2
= ( х2 – х1)2 + ( y2 – у1)2.
А(х1;у1)
В(х2;у2)
Слайд 9
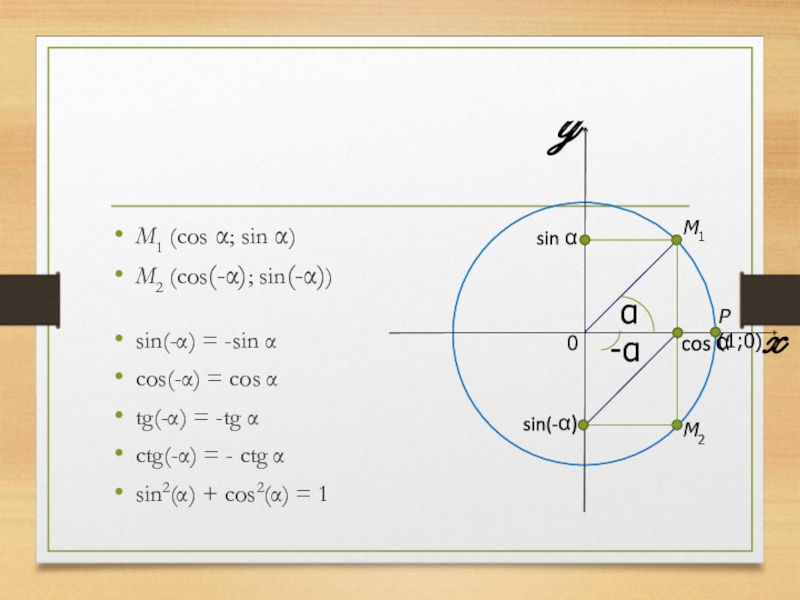
M1 (cos α; sin α)
M2 (cos(-α); sin(-α))
sin(-α) = -sin α
cos(-α) =
cos α
tg(-α) = -tg α
ctg(-α) = - ctg α
sin2(α) + cos2(α) = 1
tg(-α) = -tg α
ctg(-α) = - ctg α
sin2(α) + cos2(α) = 1
x
y
P (1;0)
0
α
-α
M2
M1
cos α
sin(-α)
sin α
Слайд 10Теорема Для любых α и β справедливо равенство cos(α + β)
= cos α cos β – sin α sin β
По определению:
Mα (cos α; sin α)
M-β (cos(-β); sin(-β))
Mα+β (cos(α+β); sin(α+β))
∠M0OMα+β = ∠M-βOMα
⇒ △M0OMα+β = △M-βOMα
⇒ основания M0Mα+β = M-βMα равны
А значит равны (M-βMα)2 и (M0Mα+β)2, запишем их
x
y
M0(1;0)
0
Mα
M-β
Mα+β
Слайд 11Теорема
Имеем:
M0 (1; 0)
M-β (cos(-β); sin(-β))
Mα (cos α; sin α) Mα+β (cos(α+β); sin(α+β))
(M0Mα+β)2 = (M-βMα)2
⇒ (1 - cos(α+β))2 +(sin(α+β))2 = (cos(-β) - cos α)2 + (sin(-β) - sin α)2
⇔ 1 - 2cos(α+β) + cos2(α+β) + sin2(α+β) = cos2 β - 2cos β cos α + cos2 α + sin2 β + 2sin β sin α + sin2 α
⇔ 2 - 2cos(α+β) = 2 - 2cos α cos β + 2sin α sin β
⇔ cos(α+β) = cos α cos β - sin α sin β
Теорема доказана.
Mα (cos α; sin α) Mα+β (cos(α+β); sin(α+β))
(M0Mα+β)2 = (M-βMα)2
⇒ (1 - cos(α+β))2 +(sin(α+β))2 = (cos(-β) - cos α)2 + (sin(-β) - sin α)2
⇔ 1 - 2cos(α+β) + cos2(α+β) + sin2(α+β) = cos2 β - 2cos β cos α + cos2 α + sin2 β + 2sin β sin α + sin2 α
⇔ 2 - 2cos(α+β) = 2 - 2cos α cos β + 2sin α sin β
⇔ cos(α+β) = cos α cos β - sin α sin β
Теорема доказана.
Слайд 12Запомните!
cos(α + β) = cosα cosβ – sinαsinβ ;
Следствия:
cos(α - β)
= cosα cosβ + sinα sinβ
sin(α + β) = sin α cos β + cos α sin β
sin(α - β) = sin α cos β - cos α sin β
sin(α + β) = sin α cos β + cos α sin β
sin(α - β) = sin α cos β - cos α sin β
Слайд 147. Итоги урока
Итак, сегодня на уроке мы вывели формулы для нахождения
косинуса суммы и разности двух углов, отработали навыки применения этих формул при вычислении и выполнении преобразований тригонометрических выражений, оценили уровень усвоения нового материала.