М.В.ЛОМОНОСОВ
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по алгебре Метод интервалов
Содержание
- 1. Презентация к уроку по алгебре Метод интервалов
- 2. РЕШИТЕ НЕРАВЕНСТВА:А) x2-7x+12>0 1) y= x2-7x+12 -
- 3. Б) (x-5)(x+6)≤0 (x-5)(x+6)= x2-5x+6x-30= x2+x-30 1) y=
- 4. Метод интервалов
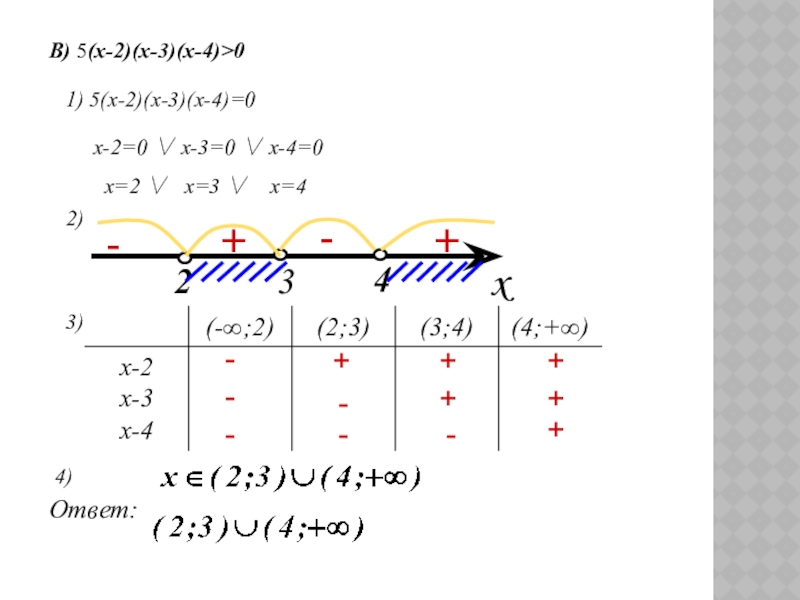
- 5. В) 5(х-2)(х-3)(х-4)>0 1) 5(х-2)(х-3)(х-4)=0
- 6. АЛГОРИТМ РЕШЕНИЯ НЕРАВЕНСТВ МЕТОДОМ ИНТЕРВАЛОВПусть требуется
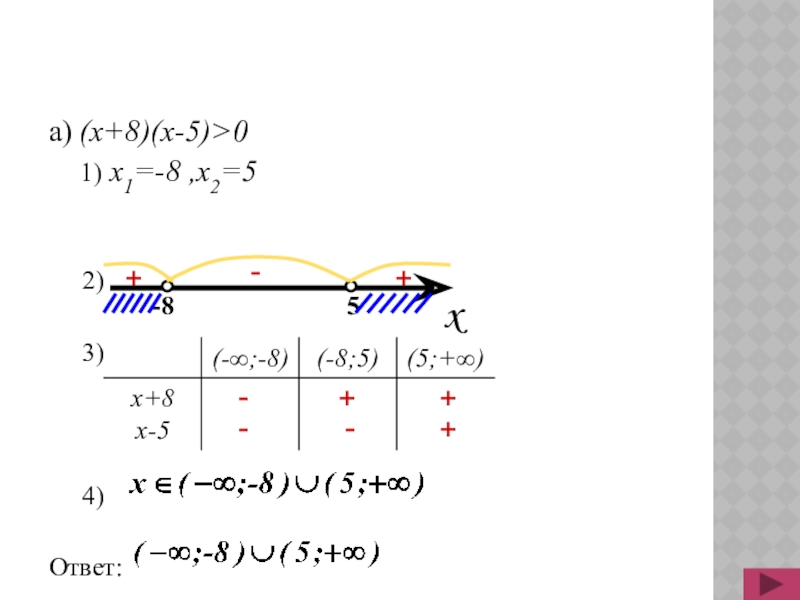
- 7. a) (x+8)(x-5)>0 1) x1=-8 ,x2=5 2) 3) 4)Ответ:--+-+++-+
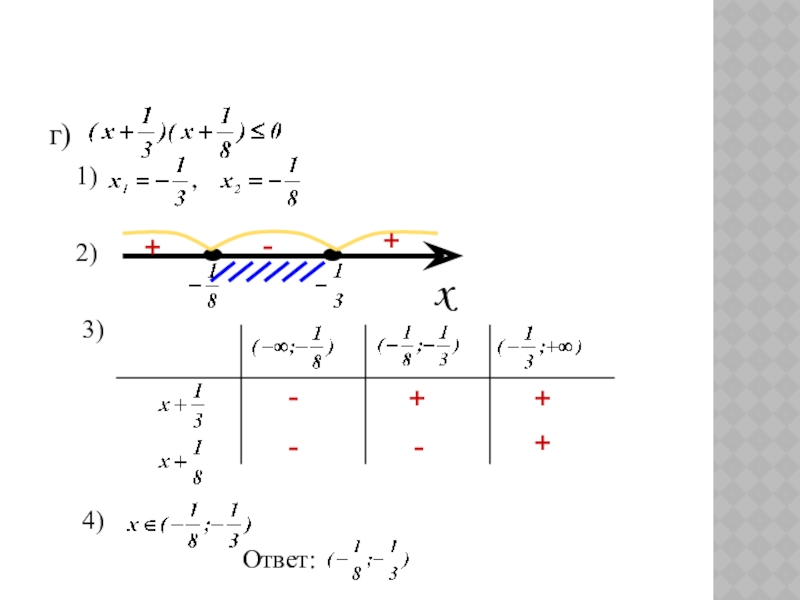
- 8. г) 1) 2)
РЕШИТЕ НЕРАВЕНСТВА:А) x2-7x+12>0 1) y= x2-7x+12 - квадратичная функция, график – квадратичная парабола,
Слайд 2РЕШИТЕ НЕРАВЕНСТВА:
А) x2-7x+12>0
1) y= x2-7x+12 - квадратичная функция,
график – квадратичная парабола,
ветви направлены вверх.
2) x2-7x+12=0
по т.Виета
3)
+ - +
Ответ:
ветви направлены вверх.
2) x2-7x+12=0
по т.Виета
3)
+ - +
Ответ:
Слайд 3Б) (x-5)(x+6)≤0
(x-5)(x+6)= x2-5x+6x-30= x2+x-30
1) y= x2+x-30 - квадратичная функция,
график – квадратичная парабола,
ветви направлены вверх.
2) x2+x-30 =0
x1=5, x2=-6
3)
+ - +
Ответ:
ветви направлены вверх.
2) x2+x-30 =0
x1=5, x2=-6
3)
+ - +
Ответ:
Слайд 5В) 5(х-2)(х-3)(х-4)>0
1) 5(х-2)(х-3)(х-4)=0
x-2=0 ∨ x-3=0
∨ x-4=0
x=2 ∨ x=3 ∨ x=4
2)
3)
4)
Ответ:
x=2 ∨ x=3 ∨ x=4
2)
3)
4)
Ответ:
+
-
+
-
-
-
-
+
-
+
+
+
+
+
-
-
Слайд 6АЛГОРИТМ РЕШЕНИЯ НЕРАВЕНСТВ
МЕТОДОМ ИНТЕРВАЛОВ
Пусть требуется решить неравенство
а(х - х1) (х
- х2)(х – х3)…(x - xn) < 0, где х1 < х2 < х3 < … < xn
1. Найти корни уравнения
а(х - х1) (х - х2)(х – х3)…(x - xn) = 0
Отметить на числовой прямой корни х1 , х2 , х3 ,… , xn
Определить знак выражения
а(х - х1) (х - х2)(х – х3)…(x - xn)
на каждом из получившихся промежутков.
4. Записать ответ, выбрав промежутки с соответствующим знаку неравенства знаком .
1. Найти корни уравнения
а(х - х1) (х - х2)(х – х3)…(x - xn) = 0
Отметить на числовой прямой корни х1 , х2 , х3 ,… , xn
Определить знак выражения
а(х - х1) (х - х2)(х – х3)…(x - xn)
на каждом из получившихся промежутков.
4. Записать ответ, выбрав промежутки с соответствующим знаку неравенства знаком .