- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку математики на тему Прогрессии (9класс)
Содержание
- 1. Презентация к уроку математики на тему Прогрессии (9класс)
- 2. Легенда
- 3. Древнеиндийский царь Шерам пожелал наградить изобретателя шахмат древнеиндийского ученого Сету.
- 4. « Я достаточно богат, чтобы исполнить любое твое пожелание, проси, что хочешь»заявил самонадеянный царь
- 5. «Прикажи выдать за первую клетку шахматной доски
- 6. «Довольно, ты получишь зерна за все 64
- 7. Ученый Сета улыбнулся, поклонился и ушел дожидаться обещанной награды
- 8. Наутро царь осведомился у слуг, доставлена ли
- 9. «Не в твоей власти исполнять такие желания,
- 10. Восемнадцать квинтильонов четыреста сорок шесть квадрильонов семьсот
- 11. Сами по себе прогрессии известны так давно,
- 12. Арифметическая прогрессия ……………:Числовая последовательность, каждый член которой,
- 13. Геометрическая прогрессияЧисловая последовательность, каждый член которой, начиная
- 14. Определение
- 15. Отражается ли окружающий мир в зеркале математических прогрессий
- 16. Что выгоднее…100 000 $ 1 цент илиПрямо сейчасЕжедневно удваивающийся в течение 28 дней
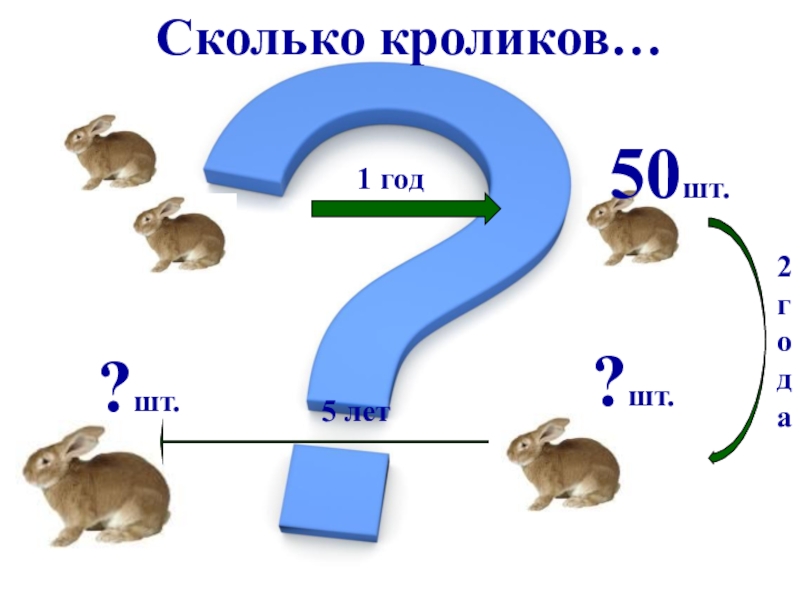
- 17. Сколько кроликов…50шт.1 год2года?шт. 5 лет?шт.
- 18. За какое время…Слышали новость…1 час?ч1296 человекСлышали новость…?чг.Талица, ≈30 000 чел
- 19. Задача для наблюдательных…г.Оклэнд, Новая Зеландия
- 20. Спасибо за внимание!Желаю вам успехов в движении вперед!Информационные источникиАлимов Ш. Алгебра 9.М.:2000Перельман Я.И. Живая математика.М.:1978http://festival.1september.ruhttp://nz.net.ruhttp://images.yandex.ru
Слайд 3
Древнеиндийский царь Шерам пожелал наградить изобретателя
Слайд 4
« Я достаточно богат, чтобы исполнить любое твое пожелание, проси, что
заявил самонадеянный царь
Слайд 5
«Прикажи выдать за первую клетку шахматной доски одно пшеничное зерно, за
Слайд 6
«Довольно, ты получишь зерна за все 64 клетки доски согласно твоему
раздраженно сказал самоуверенный царь Шерам
Слайд 8Наутро царь осведомился у слуг, доставлена ли награда изобретателю
« О
«Как бы оно не было велико,
награда должна быть выдана,
не жалейте амбаров зерна»-
надменно ответил слугам царь
Слайд 9«Не в твоей власти исполнять такие желания, во всех твоих амбарах
«Назовите же мне это чудовищное число» -
воскликнул изумленный царь
Слайд 10Восемнадцать квинтильонов четыреста сорок шесть квадрильонов семьсот сорок четыре триллиона семьдесят
Слайд 11Сами по себе прогрессии известны так давно, что трудно сказать кто
На связь между прогрессиями первым обратил внимание великий Архимед (ок.287-212до н.э)
С первой формулой связана одна из страниц биографии Карла Гаусса. Уже в 3 классе он моментально нашел сумму всех натуральных чисел от 1 до 100.
Первые формулы прогрессий появились в учебнике Магницкого Л.Ф. «Арифметика», изданного 200 лет назад.
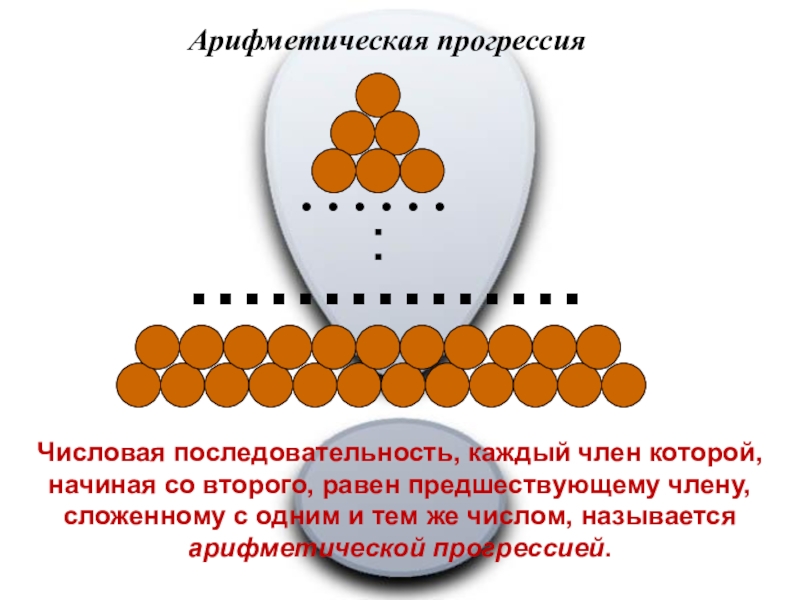
Слайд 12Арифметическая прогрессия
……………
:
Числовая последовательность, каждый член которой, начиная со второго, равен
……
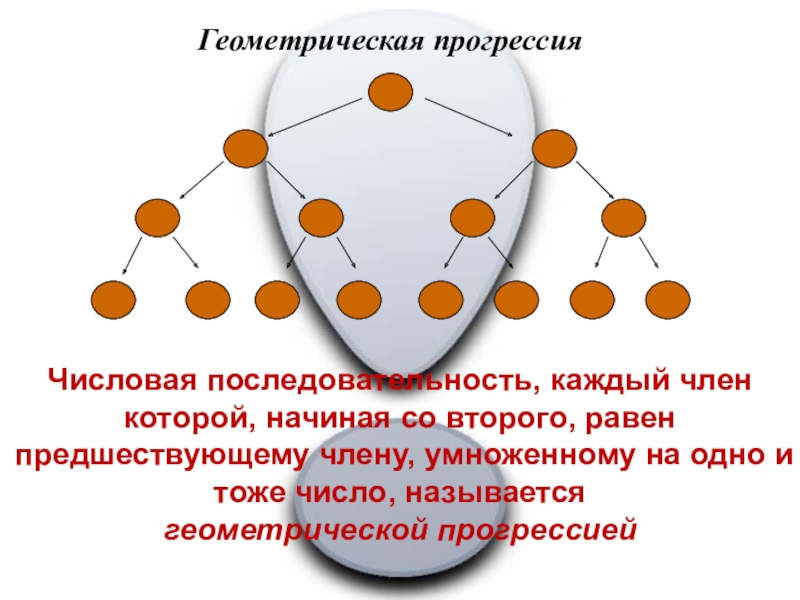
Слайд 13Геометрическая прогрессия
Числовая последовательность, каждый член которой, начиная со второго, равен предшествующему
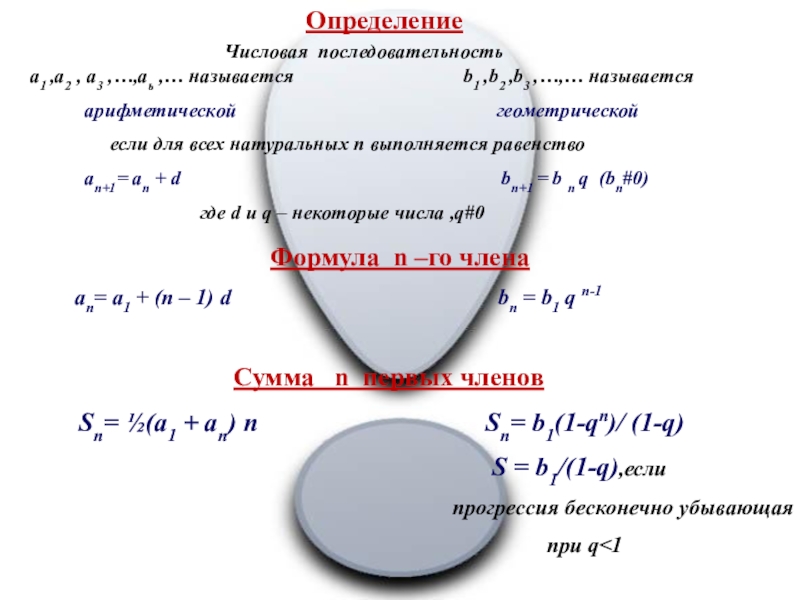
Слайд 14Определение
арифметической геометрической
если для всех натуральных n выполняется равенство
an+1= an + d bn+1 = b n q (bn#0)
где d и q – некоторые числа ,q#0
Формула n –го члена
an= a1 + (n – 1) d bn = b1 q n-1
Сумма n первых членов
Sn= ½(a1 + an) n Sn= b1(1-qn)/ (1-q)
S = b1/(1-q),если
прогрессия бесконечно убывающая
при q<1
Слайд 20Спасибо за внимание!
Желаю вам успехов в движении вперед!
Информационные источники
Алимов Ш. Алгебра
Перельман Я.И.
Живая математика.М.:1978
http://festival.1september.ru
http://nz.net.ru
http://images.yandex.ru