- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Комплексные числа
Содержание
- 1. Презентация к уроку Комплексные числа
- 2. История развития чиселПервое аксиоматическое определение
- 3. Z – целые числа
- 4. Q – рациональные числа
- 5. Q – рациональные числа (quotient
- 6. R – действительные числа(real – реальный, настоящий)
- 7. В 1768 г. в своем учебнике алгебры
- 8. Впервые вплотную к
- 9. C – комплексные числа (complex
- 10. История развития чиселДолгое время даже
- 11. Слайд 11
- 12. Определение комплексного числаа – действительная (reale) часть
- 13. Для строгого определения комплексных чисел нужно ввести
- 14. Арифметические операции над комплексными числами z₁ +
- 15. Примеры1. Дано: z₁ = 1 –
- 16. Определение сопряженных комплексных чисел
- 17. Модуль комплексного числаСвойства взаимно сопряженных комплексных чисел
- 18. литератураhttp://images02.olx.ru/ui/1/28/70/6422870_1.jpg http://shimrg.rusedu.net/gallery/646/Risunok19.png http://30nar-sol6.edusite.ru/images/professhttp://external.ak.fbcdn.net/safe_image.php?d=fbf3b968482926ac6e712cd0b2fc3821&w=180&h=540&url=http%3A%2F%2Fupload.wikimedia.org%2Fwikipedia%2Fcommons%2F3%2F3a%2FGiuseppe_Peano.jpg (Пеано)http://nplit.ru/books/item/f00/s00/z0000062/pic/000021.jpg (Стевин)http://upload.wikimedia.org/wikipedia/commons/d/d9/Rhind_Mathematical_Papyrus.jpg (папирусРайнда)
- 19. http://berkovich-zametki.com/2009/Zametki/Nomer10/Karl_Weierstrass.jpg (Вейерштрасс)http://rudimatematici-lescienze.blogautore.espresso.repubblica.it/files/2010/10/Dedekind.jpg (Дедекинд)http://zhmud-s.moy.su/_si/0/70913698.jpg (Кантор)http://www.childrenpedia.org/2/18.files/image048.jpg (Эйлер)http://newton.net.pl/files/matematyka/Bombelli.jpeg (Бомбелли)http://www.sil.si.edu/digitalcollections/hst/scientific-identity/fullsize/SIL14-G001-10a.jpg (Гаусс)http://www.mightywombat.com/toons/numbers.gif
Слайд 1Комплексные числа
(Алгебра и начала математического анализа 11 класс)
Мы никогда не стали
Платон
Слайд 2 История развития чисел
Первое аксиоматическое определение
множества натуральных чисел дано
N – натуральные числа
(natural - естественный)
Слайд 3Z – целые числа
(zero – нуль)
В
История развития чисел
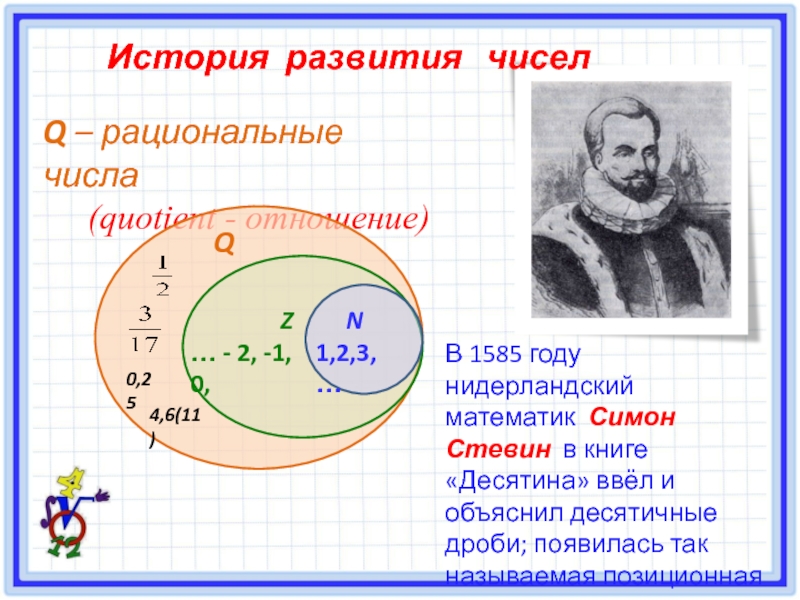
Слайд 4Q – рациональные числа
(quotient - отношение)
В древнеегипетском
История развития чисел
Слайд 5Q – рациональные числа
(quotient - отношение)
В 1585 году
История развития чисел
Слайд 6R – действительные числа
(real – реальный, настоящий)
Математическое строгое
История развития чисел
Слайд 7В 1768 г. в своем учебнике алгебры Леонард Эйлер писал, что
История развития чисел
i
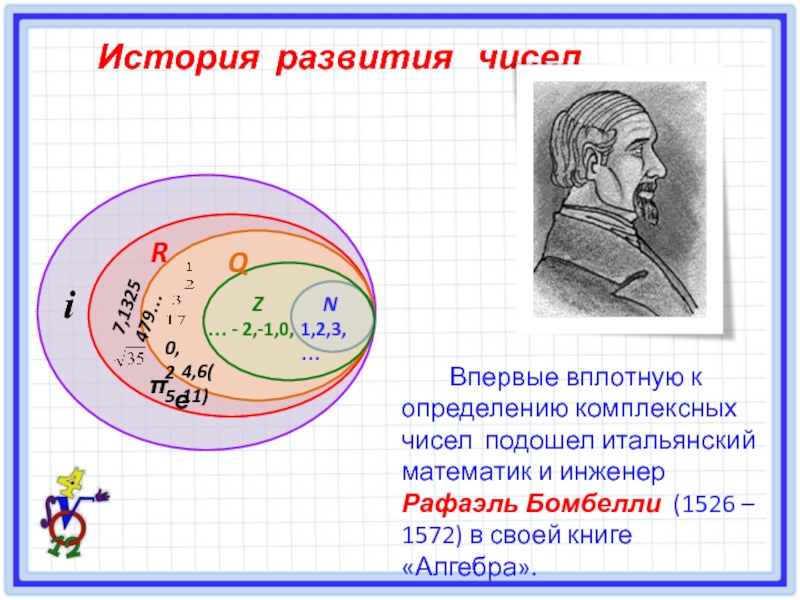
Слайд 8 Впервые вплотную к определению комплексных чисел подошел
История развития чисел
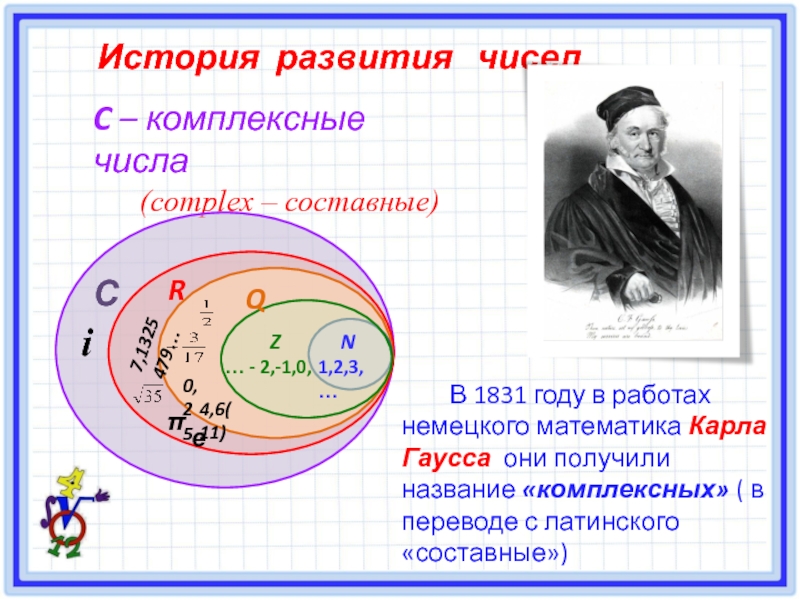
Слайд 9C – комплексные числа
(complex – составные)
История развития чисел
Слайд 10 История развития чисел
Долгое время даже математики считали комплексные числа
Около 1800-го года сразу несколько математиков (Вессель, Арган, Гаусс) поняли, что комплексными числами можно моделировать векторные величины на плоскости.
Слайд 12Определение комплексного числа
а – действительная (reale) часть комплексного числа
а =
b – мнимая (imaginary )часть комплексного числа
b = IM(z)
i – мнимая единица
z = bi – чисто мнимое число
z = а – действительное число
Обозначают: z = а + bi
Слайд 13Для строгого определения комплексных чисел нужно ввести для этих чисел понятие
а + bi = с + di <=> а = с, b = d
Слайд 14Арифметические операции над комплексными числами
z₁ + z₂= (а + bi)
z₁ - z₂= (а + bi) - (с + di) = (а - с) + (b – d)i
z₁ · z₂= (а + bi) · (с + di) = (а с - bd) + (bс + аd)i
Доказательство:
z₁ · z₂ = (а + bi) · (с + di) = ас + аdi + bсi + bdi² =
= (а с - bd) + (bс + аd)i
Слайд 15Примеры
1. Дано: z₁ = 1 – 2i
z3 = - 7i
Вычислить: а) z₁ · z₂
б) z₁ + z₂ · z3
в) z₁ ( z₂ -z3)
г) z₁ + (z₂ )² +(z3)²
2.