значения функции.
Четность, нечетность функции
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку алгебры в 9 кл
Содержание
- 1. Презентация к уроку алгебры в 9 кл
- 2. Четные и нечетные функции
- 3. Найдите область определения функции:3) f(x) =2х3f(x) = х2
- 4. Если числовое множество Х вместе с каждым
- 5. 3) f(x) =2х3f(x) = х2 симметричные множестване симметричные множества
- 6. Определение 1.Функция у = f (х) называется
- 7. Алгоритм исследования функции у=f(х) на четность
- 8. Выполните:№277(а)№278(а)№281- устно
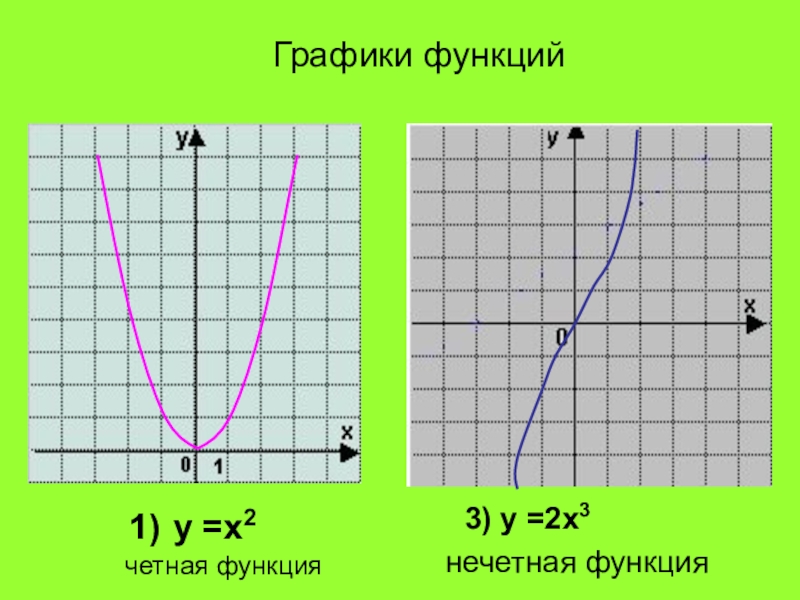
- 9. у =х2 3) у =2х3Графики функцийчетная функциянечетная функция
- 10. График четной функции симметричен относительно оси ординат(оси у)График нечетной функции симметричен относительно начала координат
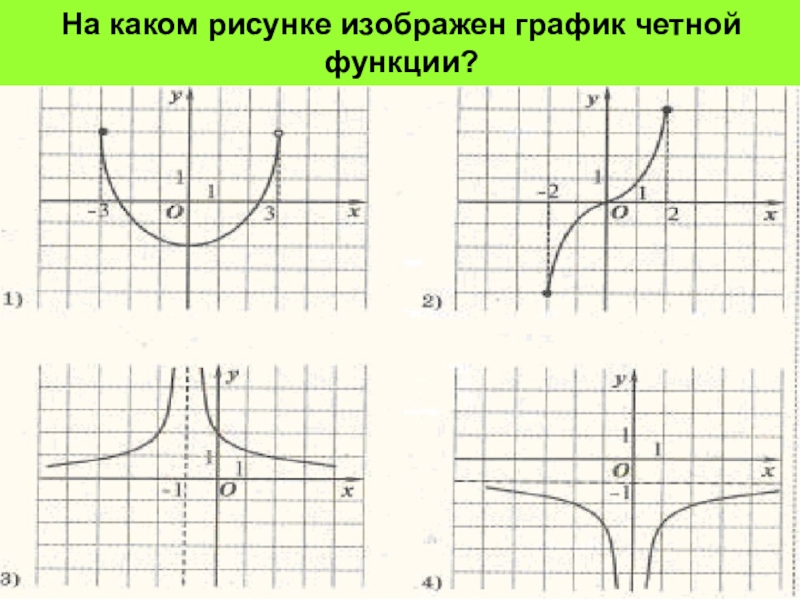
- 11. На каком рисунке изображен график четной функции?
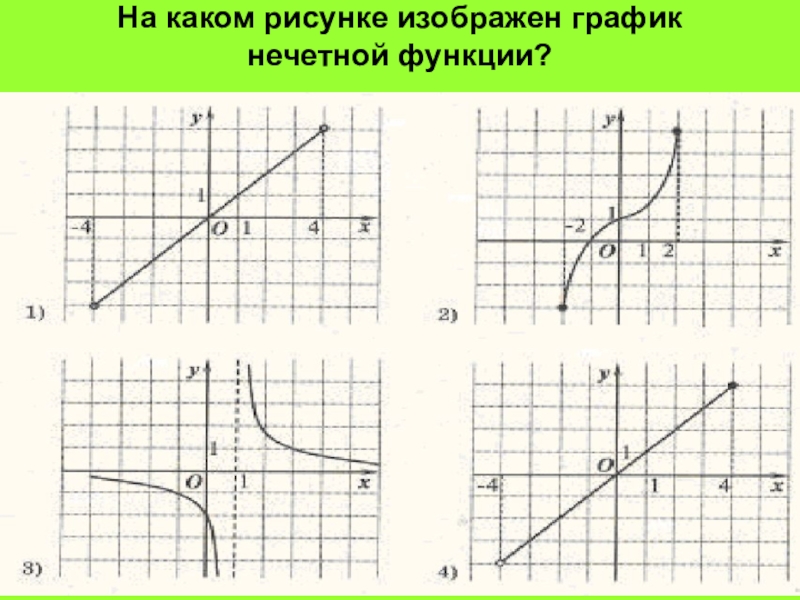
- 12. На каком рисунке изображен график нечетной функции?
- 13. Памятка 21.Функция f(x) называется чётной,
- 14. Спасибо за урок!
Четные и нечетные функции
Слайд 1Свойства функций
Область определения функции;
Промежутки монотонности;
Ограниченность функции;
Наибольшее, наименьшее значения функции;
Непрерывность функции;
Выпуклость функции;
Область
Слайд 4Если числовое множество Х вместе с каждым своим элементом х содержит
и противоположный элемент –х, то Х называют симметричным множеством
Например:(-2;2), [-5;5]
симметричные множества
(-2;3), [-5;5)
не симметричные множества
Слайд 6Определение 1.
Функция у = f (х) называется чётной, если для любого
значения х из области определения f(-x)= f(x)
Определение 2.
Функция у = f(х) называется нечётной, если для любого значения х из области определения f (-x)= -f(x)
Слайд 7Алгоритм исследования функции
у=f(х) на четность
Установить, симметрична ли область определения функции.
Если нет, то объявить, что функция не является ни четной, ни нечетной. Если да, то переходить ко второму шагу алгоритма.
Найти f(-х).
Сравнить f(-x) и f(x):
А) Если f(-x) = f(x), то функция – четная;
Б) Если f(-x) = -f(x), то функция – нечетная;
В) Если хотя бы в одной точке х Х выполняется соотношение и хотя бы в одной точке х Х выполняется соотношение , то функция не является ни четной,
ни нечетной.
Найти f(-х).
Сравнить f(-x) и f(x):
А) Если f(-x) = f(x), то функция – четная;
Б) Если f(-x) = -f(x), то функция – нечетная;
В) Если хотя бы в одной точке х Х выполняется соотношение и хотя бы в одной точке х Х выполняется соотношение , то функция не является ни четной,
ни нечетной.
Слайд 10График четной функции симметричен относительно оси ординат(оси у)
График нечетной функции симметричен
относительно начала координат
Слайд 13Памятка 2
1.Функция f(x) называется чётной, если область её
определения симметрична относительно ____________________ и для любого значения аргумента х верно равенство f(-x) = __________
2. Функция f(x) называется нечётной, если область её определения симметрична относительно____________ и для любого значения аргумента х верно равенство f(-x) = __________
3. График любой чётной функции симметричен относительно__________________
4. График любой нечётной функции симметричен относительно__________________
2. Функция f(x) называется нечётной, если область её определения симметрична относительно____________ и для любого значения аргумента х верно равенство f(-x) = __________
3. График любой чётной функции симметричен относительно__________________
4. График любой нечётной функции симметричен относительно__________________