того, чтобы научиться делать.
М. Горький
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку алгебры в 7 классе
Содержание
- 1. Презентация к уроку алгебры в 7 классе
- 2. Тема урока: Функции и их
- 3. Прозвенел уже звонок,Начинается урок,В путешествие пойдём,В страну
- 4. Станции:ИсторическаяТеоретическаяВычислительнаяГрафическаяФизкультурнаяКоординатная
- 5. ИСТОРИЧЕСКАЯ Понятие функции уходит своими корнями в
- 6. Когда возникли первые цивилизации, началось
- 7. Путь к современному появлению понятия функции
- 8. ТЕОРЕТИЧЕСКАЯ1.Что называется функцией или функциональной зависимостью?2.Как называются
- 9. Проверяем и оцениваемВсё верно: «5»1 или 2 ошибки: «4»3 или 4 ошибки: «3»Ошибок больше 4:
- 10. ВЫЧИСЛИТЕЛЬНАЯФункция задана формулой у=2х-5.а) как найти значение
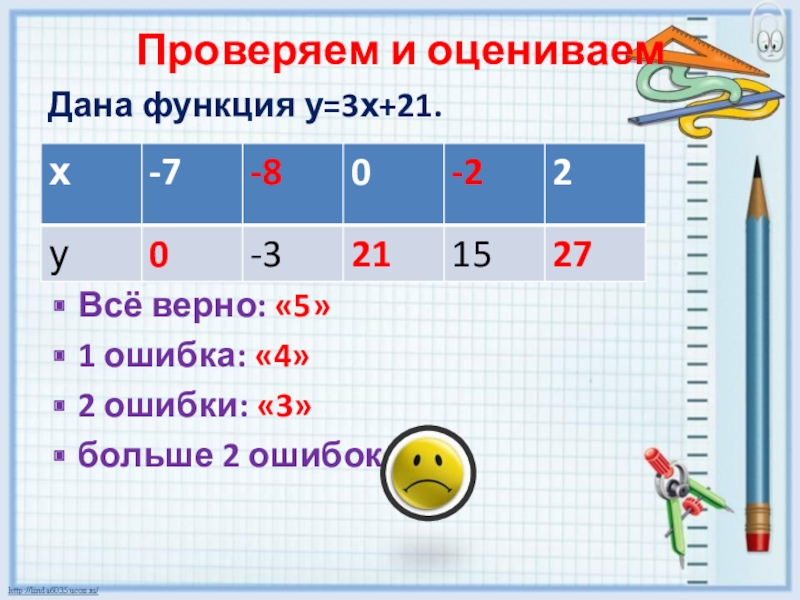
- 11. Проверяем и оцениваемДана функция у=3х+21. Всё верно: «5»1 ошибка: «4»2 ошибки: «3»больше 2 ошибок:
- 12. ГРАФИЧЕСКАЯЧто является графиком прямой пропорциональности?Что является графиком
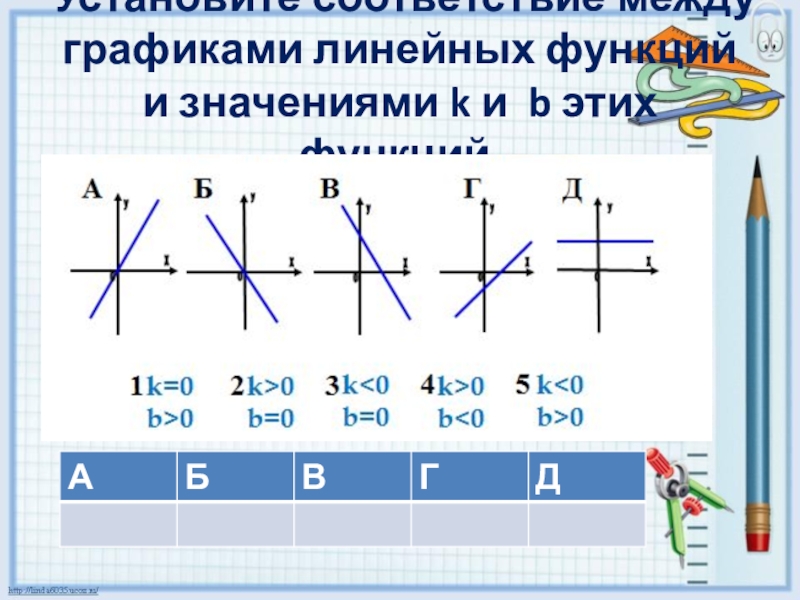
- 13. Установите соответствие между графиками линейных функций и значениями k и b этих функций.
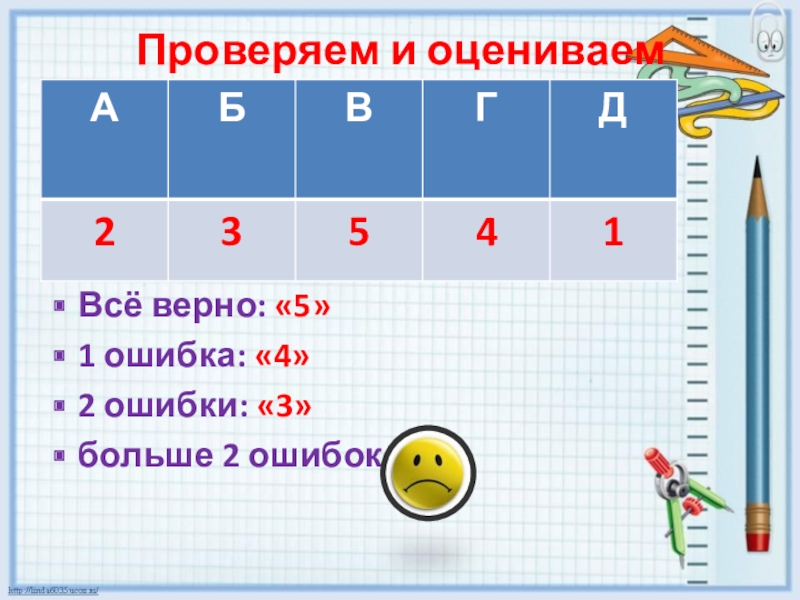
- 14. Проверяем и оцениваем Всё верно: «5»1 ошибка: «4»2 ошибки: «3»больше 2 ошибок:
- 15. КООРДИНАТНАЯКак, не выполняя построений, определить, принадлежит ли
- 16. Проверяем и оцениваем:а) нет, не пересекаются, так
- 17. Подводим итоги:Найдите среднее арифметическое всех своих отметок.на
- 18. Следующая станция КОНТРОЛЬНАЯ РАБОТА.Желаю успехов!
Тема урока: Функции и их графики. Линейная функция.Основная цель:повторить и обобщить основные знания и умения по теме «Функции. Линейная функция и её график.»
Слайд 2
Тема урока:
Функции и их графики.
Линейная функция.
Основная цель:
повторить и обобщить
основные знания и умения по теме «Функции. Линейная функция и её график.»
Слайд 3Прозвенел уже звонок,
Начинается урок,
В путешествие пойдём,
В страну функций попадём.
Слушайте, думайте, отвечайте,
Все
задания решайте,
Постарайтесь, потрудитесь
И, конечно, не ленитесь!
Постарайтесь, потрудитесь
И, конечно, не ленитесь!
Слайд 5ИСТОРИЧЕСКАЯ
Понятие функции уходит своими корнями в ту далекую эпоху, когда
люди впервые поняли, что окружающие их явления взаимосвязаны. Они еще не умели считать, но уже знали, что, чем больше оленей удастся убить на охоте, тем дольше племя будет избавлено от голода, чем дольше горит костер, тем теплее будет в пещере.
Слайд 6
Когда возникли первые цивилизации, началось строительство гигантских пирамид, понадобились
писцы, которые учитывали поступающие налоги, определяли количество кирпичей, необходимое для возведения дворцов, подсчитывали, сколько продовольствия надо заготовить для дальних походов.
Слайд 7 Путь к современному появлению понятия функции заложили в 17 веке
французские ученые Франсуа Виет и Рене Декарт; они разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание.
И только в 18 веке появляется новый взгляд на функцию как на формулу, связывающую одну переменную с другой.
И только в 18 веке появляется новый взгляд на функцию как на формулу, связывающую одну переменную с другой.
Слайд 8ТЕОРЕТИЧЕСКАЯ
1.Что называется функцией или функциональной зависимостью?
2.Как называются переменные в функции?
3.Назовите основные
способы задания функций.
4.Что называется графиком функции?
5.Какие функции вы знаете?
6.Какая функция называется прямой пропорциональностью?
7.Что является графиком прямой пропорциональности?
8.Какая функция называется линейной?
9. Что является графиком линейной функции?
4.Что называется графиком функции?
5.Какие функции вы знаете?
6.Какая функция называется прямой пропорциональностью?
7.Что является графиком прямой пропорциональности?
8.Какая функция называется линейной?
9. Что является графиком линейной функции?
Слайд 10ВЫЧИСЛИТЕЛЬНАЯ
Функция задана формулой у=2х-5.
а) как найти значение функции, соответствующее значению аргумента,
равного 10?
б)как найти значение аргумента, при котором функция принимает значение, равное 7?
б)как найти значение аргумента, при котором функция принимает значение, равное 7?
Слайд 11Проверяем и оцениваем
Дана функция у=3х+21.
Всё верно: «5»
1 ошибка: «4»
2 ошибки:
«3»
больше 2 ошибок:
больше 2 ошибок:
Слайд 12ГРАФИЧЕСКАЯ
Что является графиком прямой пропорциональности?
Что является графиком линейной функции?
Как построить график
линейной функции?
Дайте характеристику и постройте схематически график функции:
у=3х
у=-8х
у=2х-5
у=-5х+3
у=4
у=-2
Дайте характеристику и постройте схематически график функции:
у=3х
у=-8х
у=2х-5
у=-5х+3
у=4
у=-2
Слайд 15КООРДИНАТНАЯ
Как, не выполняя построений, определить, принадлежит ли точка с указанными координатами,
данной функции, заданной формулой?
Как могут взаимно располагаться графики двух линейных функций?
В каком случае графики двух линейных функций пересекаются, а в каком случае они параллельны?
Как найти координаты точки пересечения графиков двух линейных функций?
Как могут взаимно располагаться графики двух линейных функций?
В каком случае графики двух линейных функций пересекаются, а в каком случае они параллельны?
Как найти координаты точки пересечения графиков двух линейных функций?
Слайд 16Проверяем и оцениваем:
а) нет, не пересекаются, так как угловые коэффициенты одинаковые;
б)да,
пересекаются, так как угловые коэффициенты различны;
в)(7;-1).
г)принадлежит, так как -47=-47
Всё верно: «5»
верно в) и ещё одно любое: «4»
верно всё, кроме в): «3»
другое:
в)(7;-1).
г)принадлежит, так как -47=-47
Всё верно: «5»
верно в) и ещё одно любое: «4»
верно всё, кроме в): «3»
другое:
Слайд 17Подводим итоги:
Найдите среднее арифметическое всех своих отметок.
на уроке работал активно: +0,3;
все
мои устные ответы были правильными: +0,5
среди моих ответов устно больше было правильных, чем неправильных: +0,3
Выставьте отметку в дневник.
Домашнее задание: станция «ДОМАШНЯЯ»
среди моих ответов устно больше было правильных, чем неправильных: +0,3
Выставьте отметку в дневник.
Домашнее задание: станция «ДОМАШНЯЯ»