самый
благородный,
путь подражания – это путь самый лёгкий,
и путь опыта – это путь самый горький»
Конфуций
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку алгебры в 10 классе по теме Преобразование тригонометрических выражений
Содержание
- 1. Презентация к уроку алгебры в 10 классе по теме Преобразование тригонометрических выражений
- 2. Цели урока :систематизировать знания, полученные при изучении
- 3. Разминка
- 4. Слайд 4
- 5. Преобразование тригонометрических выражений
- 6. Диктант
- 7. История возникновения тригонометрии
- 8. Тригонометрия – математическая дисциплина, изучающая зависимость между
- 9. Тригонометрия возникла из практических нужд человека. С
- 10. ВозникновениеТригонометрические функции возникли в Древней Греции в
- 11. О свойствах периодичности тригонометрических функций знал ещё
- 12. Современную форму теории тригонометрических функций и вообще
- 13. Преобразование тригонометрических выражений
- 14. Домашнее задание
Цели урока :систематизировать знания, полученные при изучении темы «Тригонометрические формулы», выделить общие методы и приёмы решения задач, указав в них стандартные приёмы, продемонстрировать технику решения как простых, так и относительно сложных задач.
Слайд 1Преобразование тригонометрических выражений
«Три пути ведут к знанию:
путь размышления – это путь
Слайд 2Цели урока :
систематизировать знания, полученные при изучении темы «Тригонометрические формулы», выделить
общие методы и приёмы решения задач, указав в них стандартные приёмы, продемонстрировать технику решения как простых, так и относительно сложных задач.
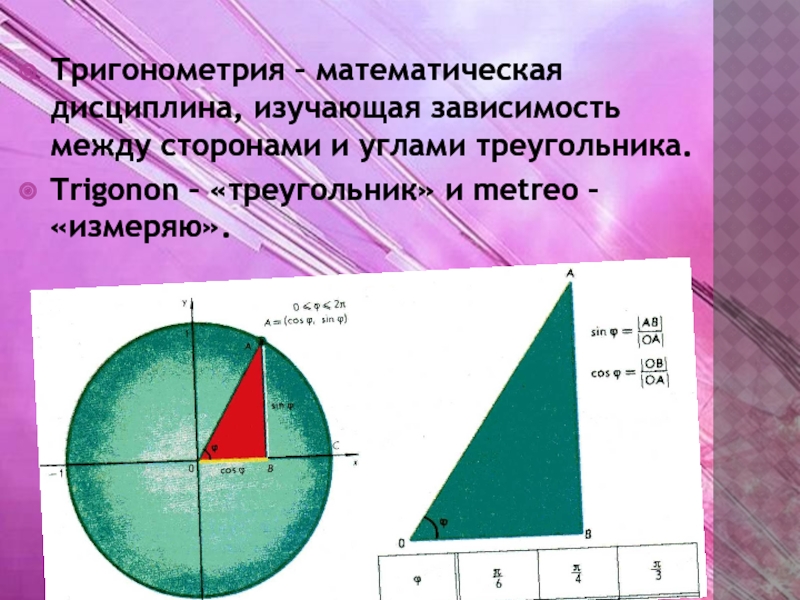
Слайд 8Тригонометрия – математическая дисциплина, изучающая зависимость между сторонами и углами треугольника.
Trigonon – «треугольник» и metreo – «измеряю».
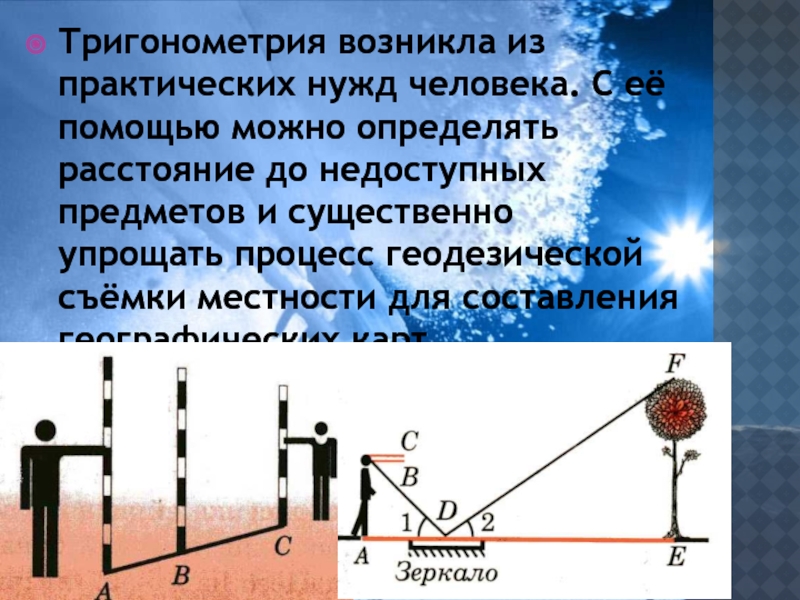
Слайд 9Тригонометрия возникла из практических нужд человека. С её помощью можно определять
расстояние до недоступных предметов и существенно упрощать процесс геодезической съёмки местности для составления географических карт.
Слайд 10Возникновение
Тригонометрические функции возникли в Древней Греции в связи с исследованиями в
астрономии и геометрии.
Отношения сторон в прямоугольном треугольнике встречались уже в III веке до нашей эры в работах Евклида, Архимеда, Аполлония Пергского и др.
Отношения сторон в прямоугольном треугольнике встречались уже в III веке до нашей эры в работах Евклида, Архимеда, Аполлония Пергского и др.
Слайд 11О свойствах периодичности тригонометрических функций знал ещё Ф. Виет. Швейцарский математик
И. Бернулли (1642-1727) в своих работах начал применять символику тригонометрических функций. Однако близкую к принятой теперь, ввел
Л. Эйлер в 1748 г. в своей работе «Введение в анализ бесконечных». В ней он рассмотрел вопрос о знаках всех тригонометрических функций любого аргумента.
Слайд 12Современную форму теории тригонометрических функций и вообще тригонометрии придал Л.Эйлер Он
ввёл в математику привычные нам формулы тригонометрии на плоскости:
Тригонометрию в средней школе изучают до сих пор по Эйлеру.
Тригонометрию в средней школе изучают до сих пор по Эйлеру.