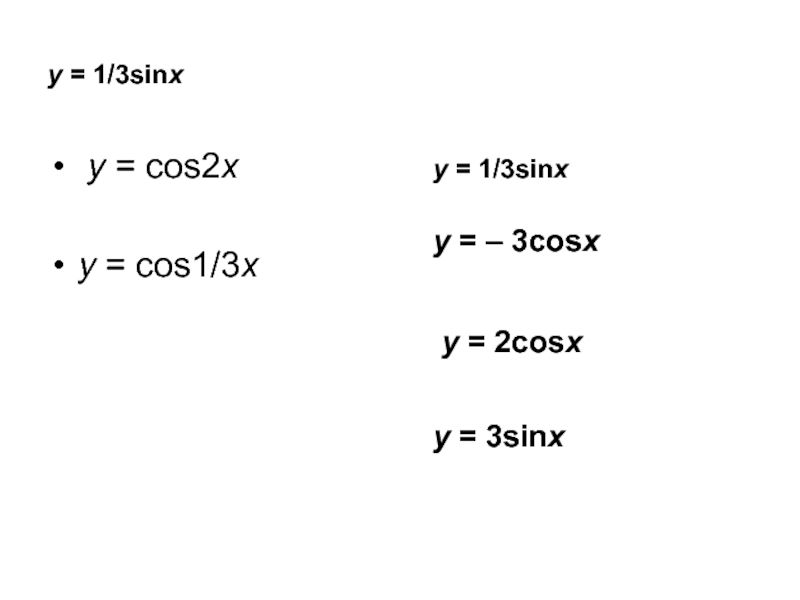- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку алгебры Преобразование графиков тригонометрических функций
Содержание
- 1. Презентация к уроку алгебры Преобразование графиков тригонометрических функций
- 2. УСТНЫЕ УПРАЖНЕНИЯ:Вычислите: sin 30˚; cos
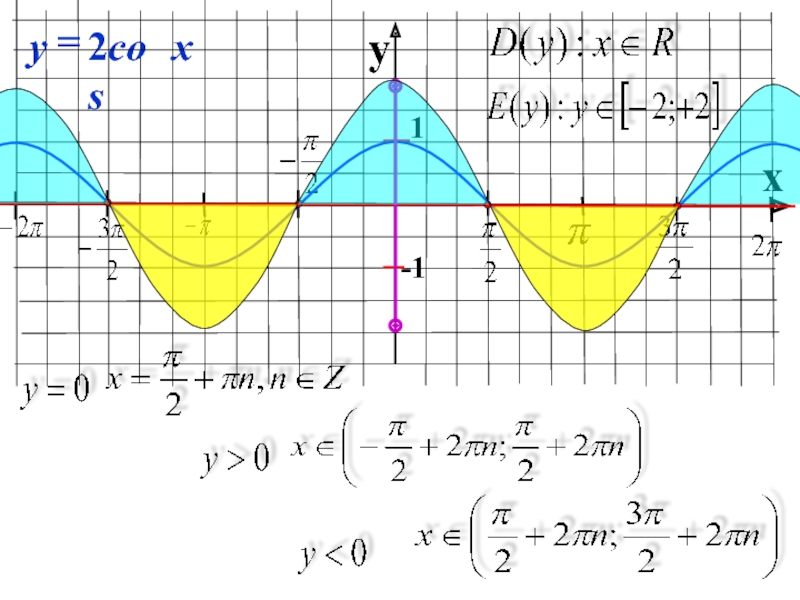
- 3. Найти область определения функции:У= sin²x + cos²xЧто является графиком функции?
- 4. Найти область значений функции:У=11sin xY= cos3xY= -5cosxY=4sinx-8Y=cos(5x-π/3)+2
- 5. Найти наибольшее целое значение функции:Y= -6,5sinxY= 4,3cosx
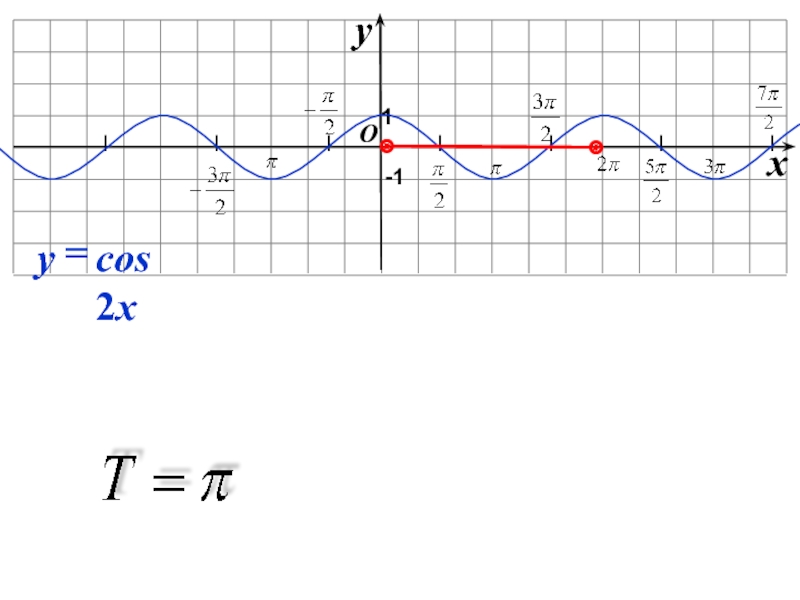
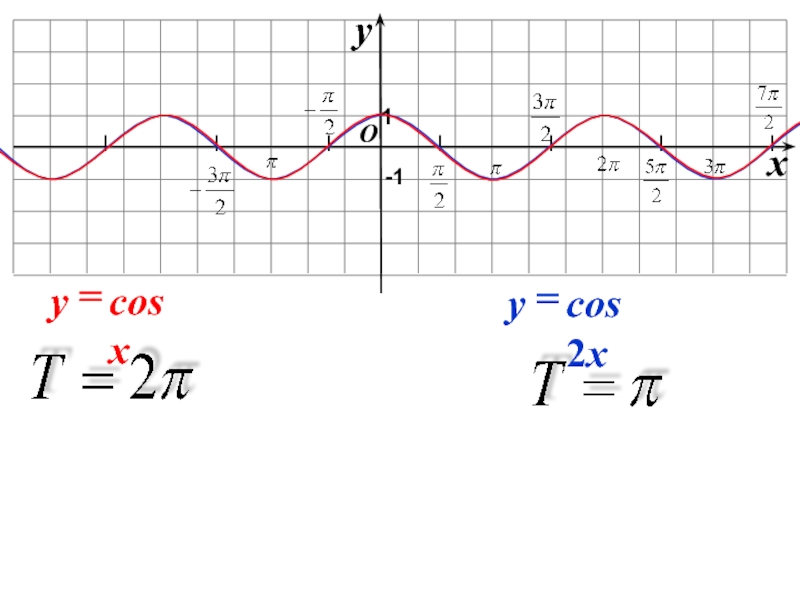
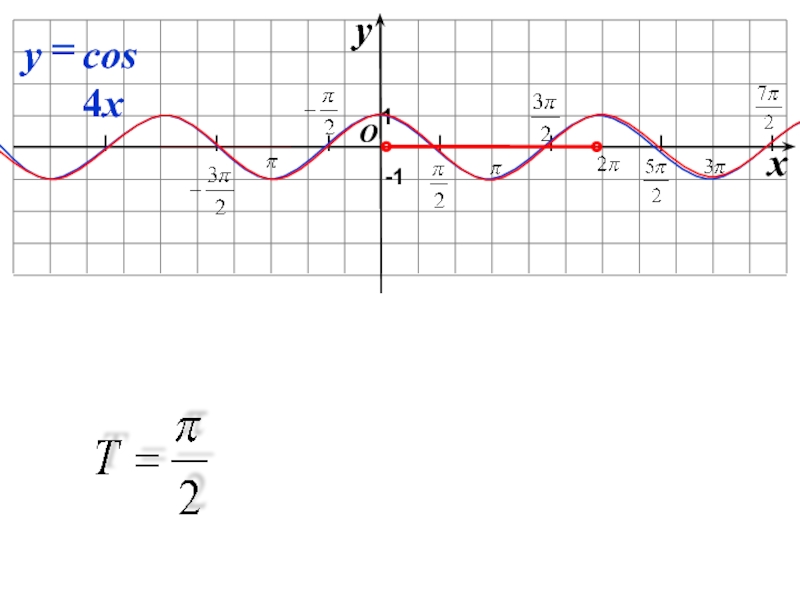
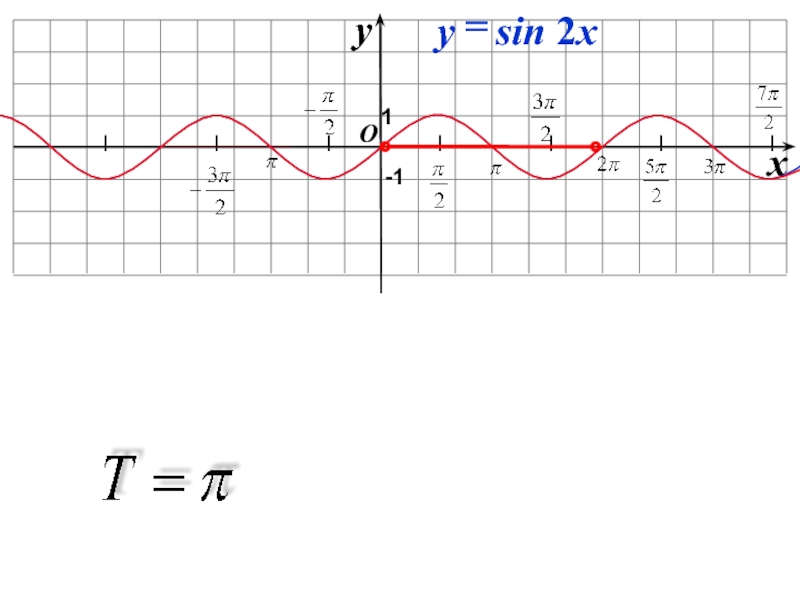
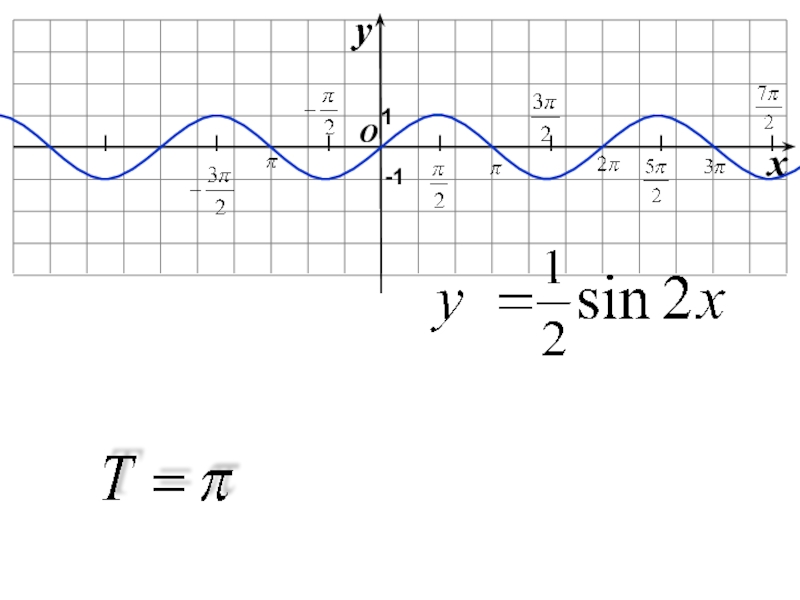
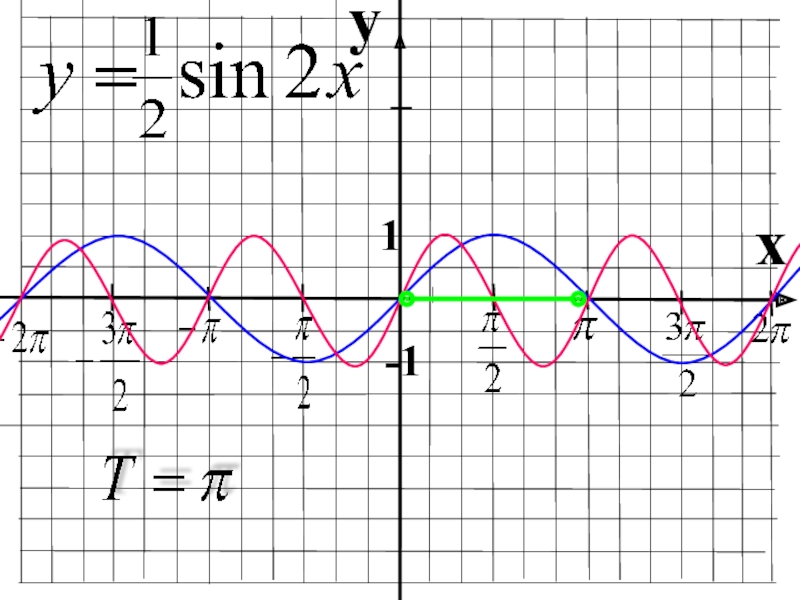
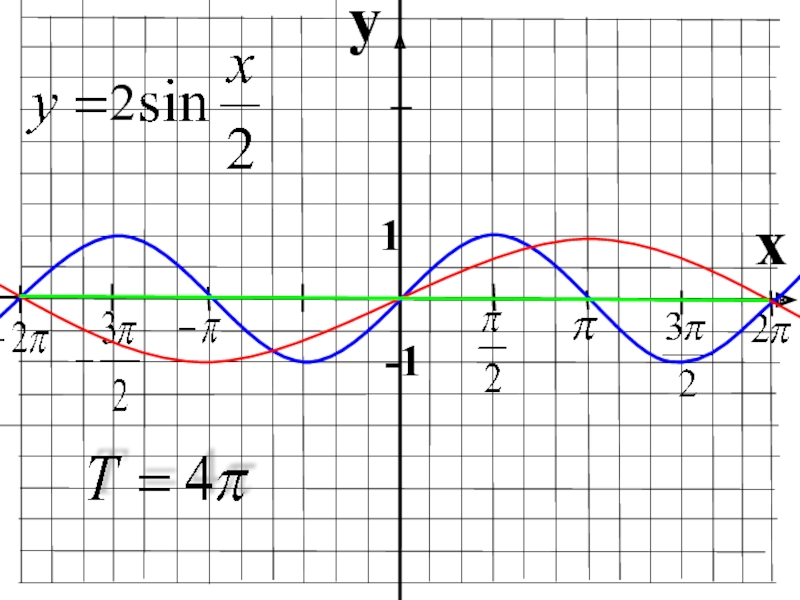
- 6. Найти период функции:Y= 2sin x/2Y=1/2 sin 2xY= cos 4xY=cos 2x
- 7. Исследуйте функцию на чётность и нечётность: f(x)= x² ·cos²a Определите знак выражения:Sin100°cos100°
- 8. Параллельный
- 9. Параллельный
- 10. Преобразование графиков тригонометрических функций
- 11. Сгруппируйте функции на две группы по какому-нибудь
- 12. изменение аргумента y = cos(x + 2); y = cos2x; y = sin(x – 5); y =
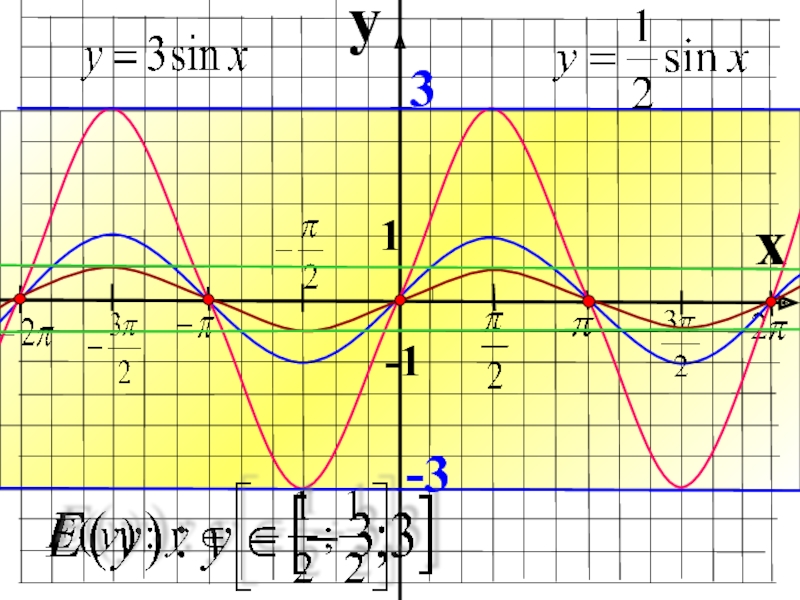
- 13. y = 1/3sinx y = cos2xy = cos1/3xy = 1/3sinx y = 2cosxy = – 3cosxy = 3sinx
- 14. Для построения графика функции y=kf(x) необходимо график
- 15. Преобразование графиков тригонометрических функций путем сжатия и
- 16. Преобразование графиков тригонометрических функций путем сжатия и растяженияy=2sinxy=4sinxY=0,5sinx
- 17. yx1-1
- 18. yx1-1IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
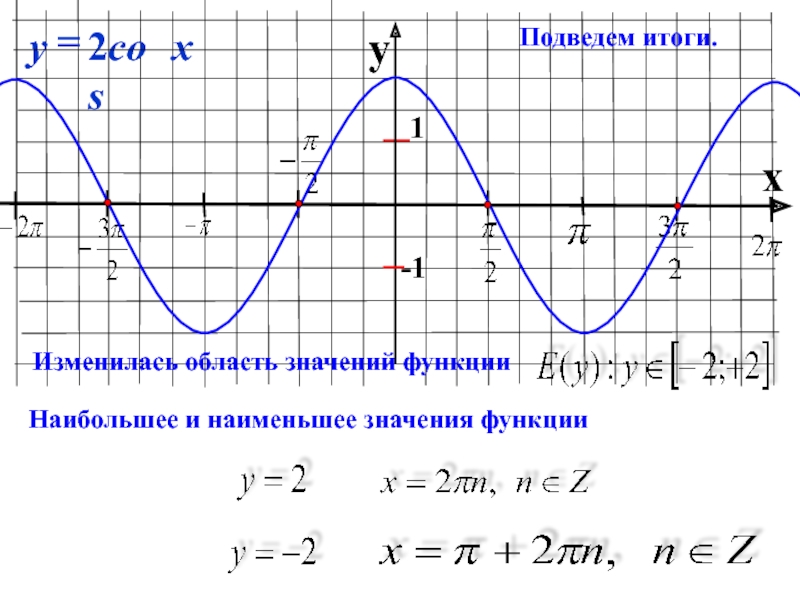
- 19. yx1-1Подведем итоги.
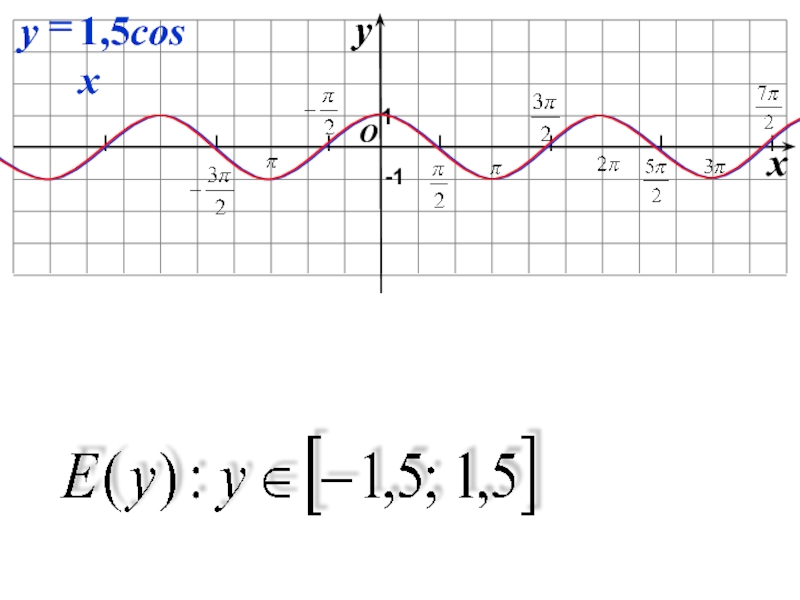
- 20. yx 1-13-3
- 21. Слайд 21
- 22. Слайд 22
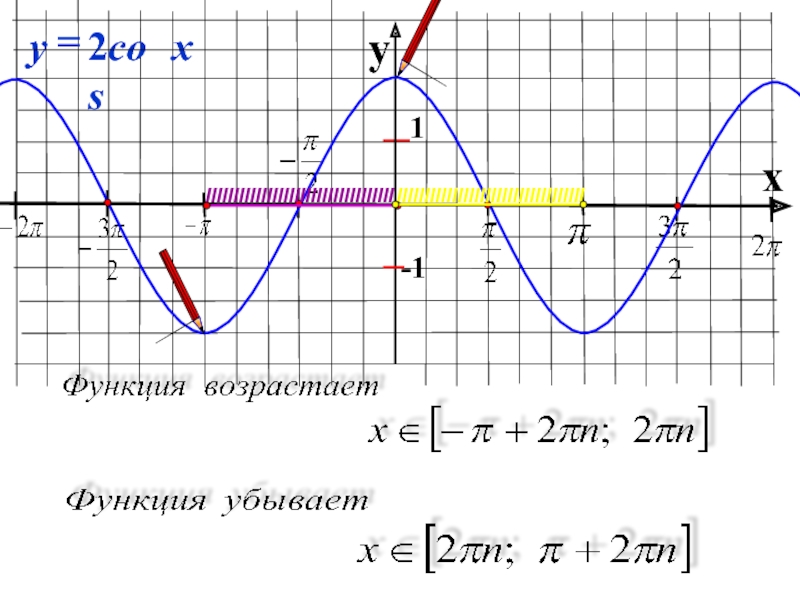
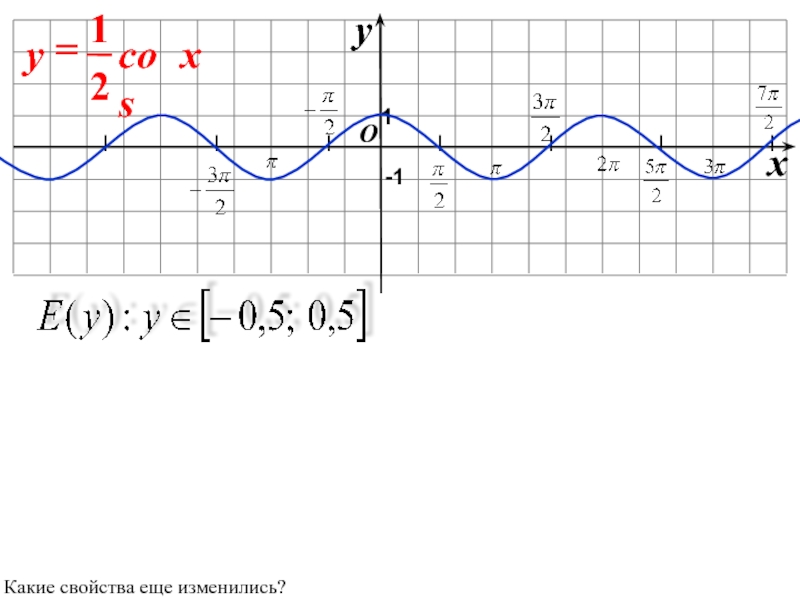
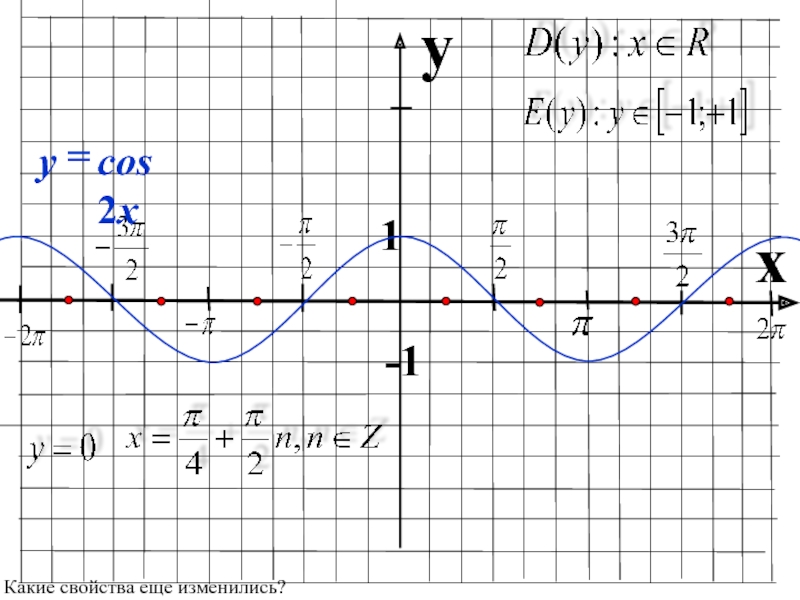
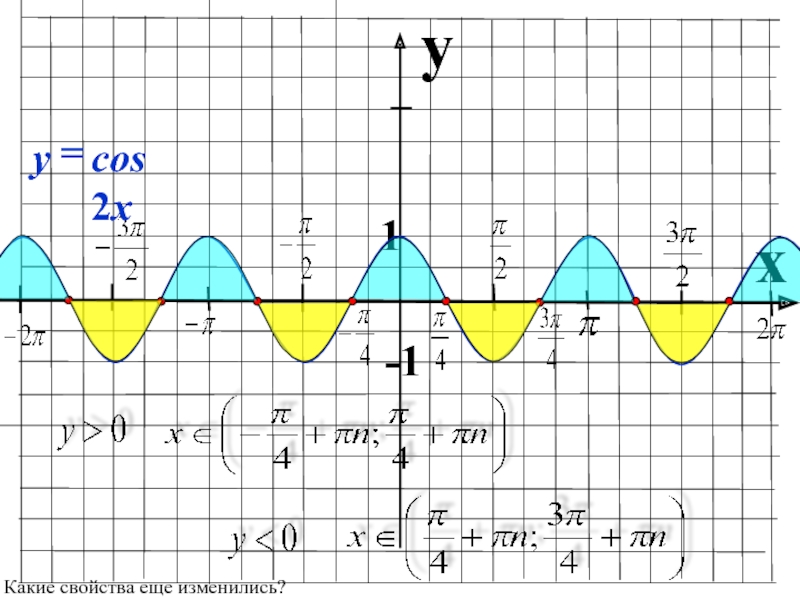
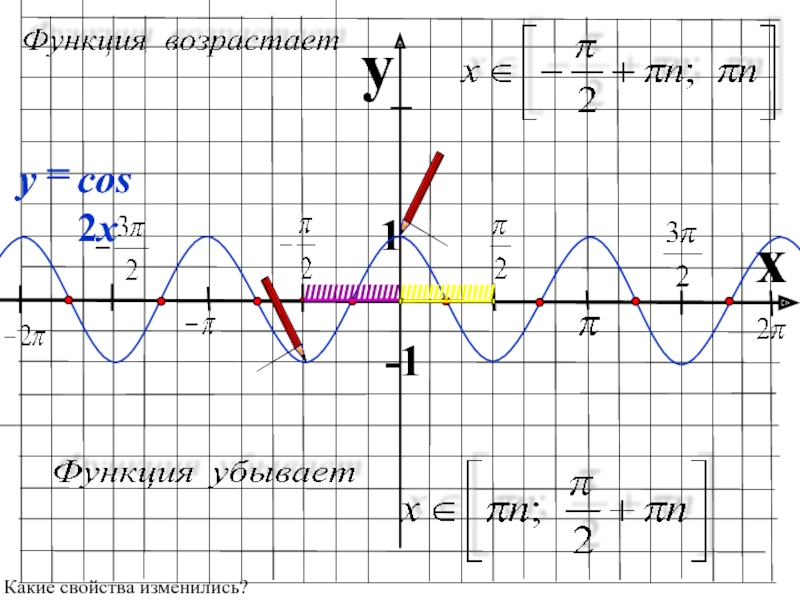
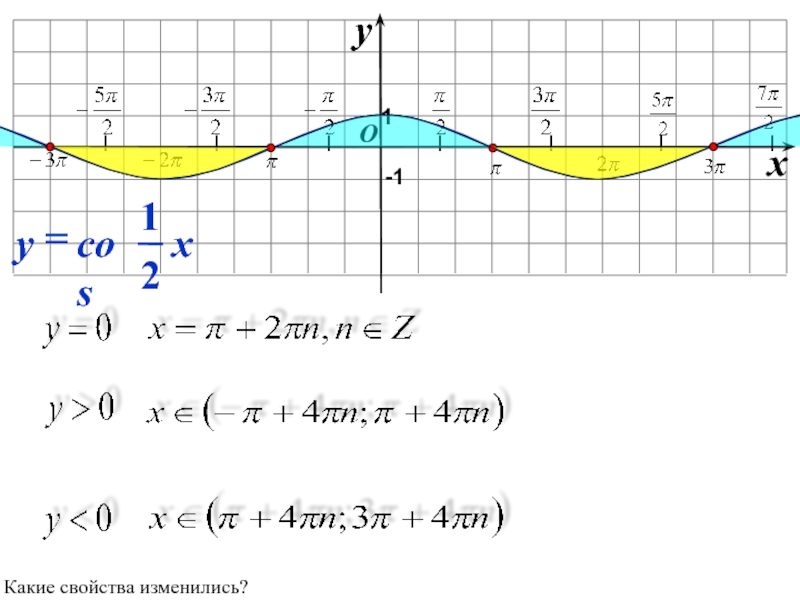
- 23. yx 1-1-1Какие свойства еще изменились?
- 24. Симметричное отображение относительно оси OY y=f(x)
- 25. Слайд 25
- 26. Слайд 26
- 27. Итог урокаНа данном уроке говорилось о …Урок
- 28. Домашнее задание.1.Среди функций выберите те, которые получаются
- 29. Растяжение (сжатие) в k раз вдоль оси
- 30. Преобразование графиков тригонометрических функций путем сжатия и
- 31. Преобразование графиков тригонометрических функций путем сжатия и растяженияy = cos2xy = cos 0.5x
- 32. Слайд 32
- 33. Слайд 33
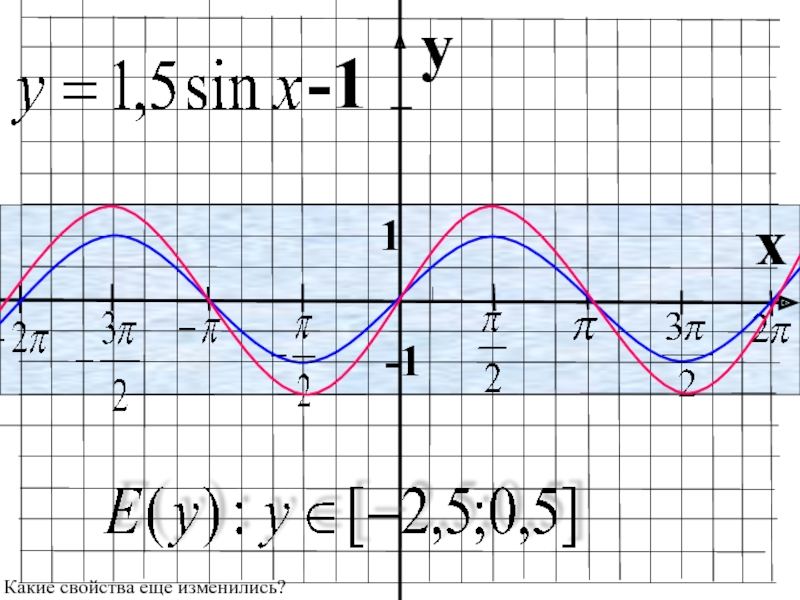
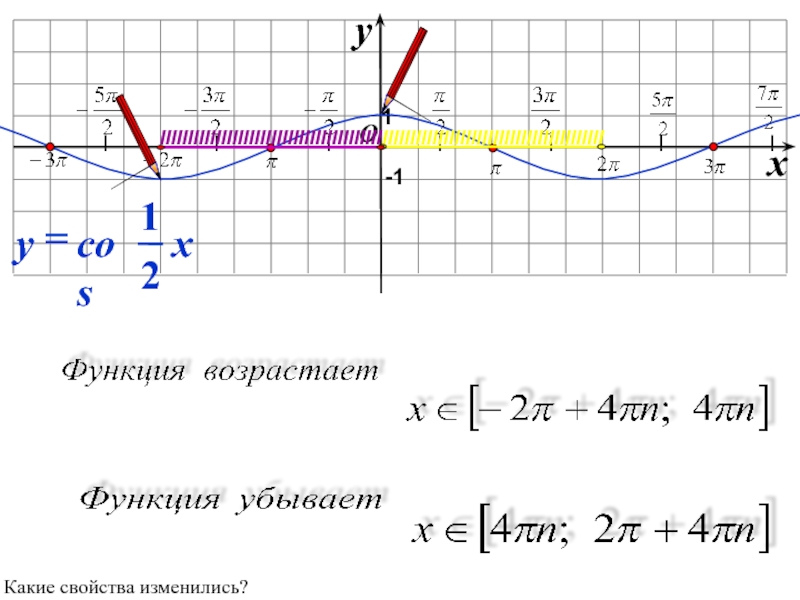
- 34. yx 1-1Какие свойства еще изменились?
- 35. yx 1-1Какие свойства еще изменились?
- 36. yx 1-1Какие свойства изменились?IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
- 37. Слайд 37
- 38. Слайд 38
- 39. Слайд 39
- 40. Слайд 40
- 41. Слайд 41
- 42. Слайд 42
- 43. Слайд 43
- 44. Слайд 44
- 45. yx 1-1
- 46. yx 1-12
- 47. Какие преобразования с синусоидой нужно выполнить, чтобы построить график данной функции?f(x)=0,5cosxf(x)=3+sinxf(x)=sin(x-п/4)f(x)=2cos(x/2+п/3)
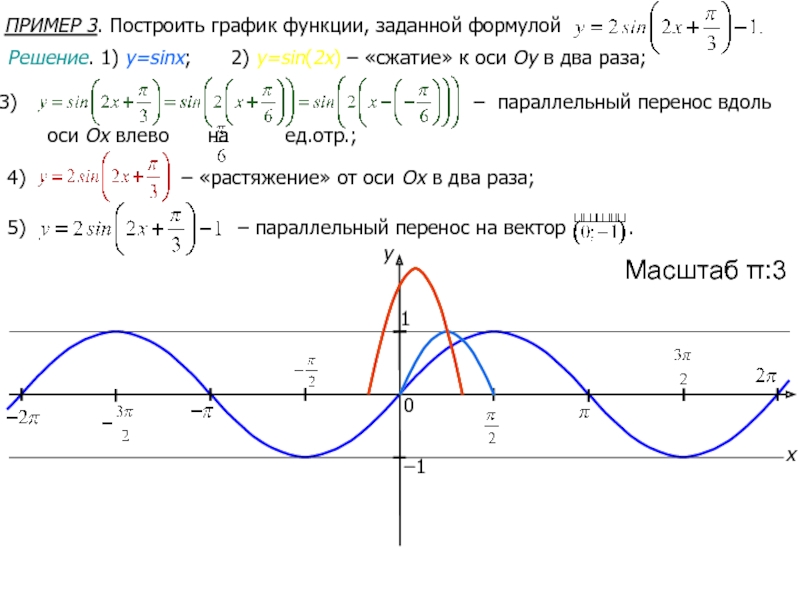
- 48. ПРИМЕР 3. Построить график функции, заданной формулой
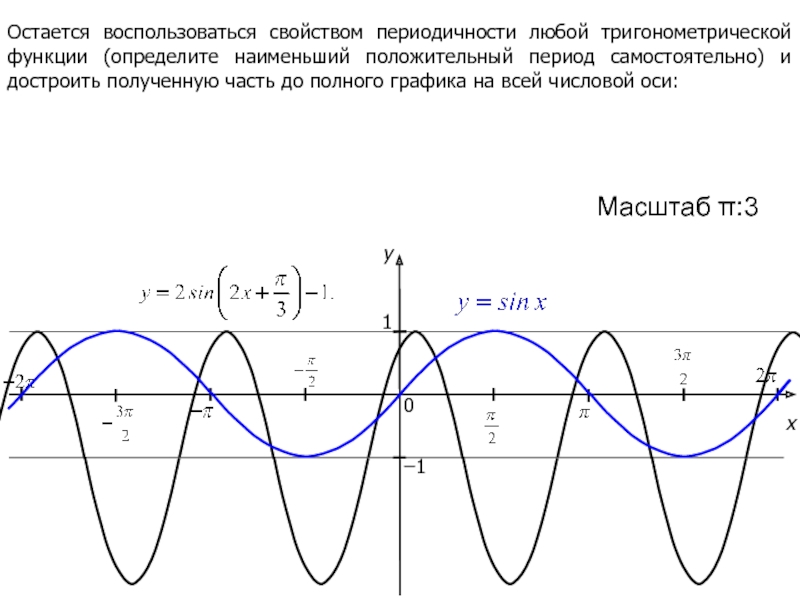
- 49. xy10Масштаб π:3−1Остается воспользоваться свойством периодичности любой тригонометрической
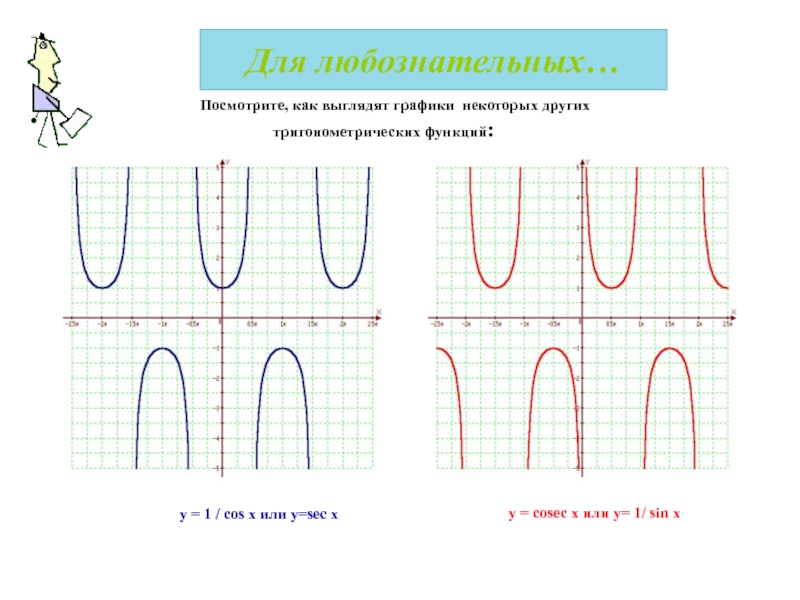
- 50. Для любознательных… Посмотрите, как выглядят графики
Слайд 2УСТНЫЕ УПРАЖНЕНИЯ:
Вычислите:
sin 30˚; cos 45˚; sin(-
tg ; cos П
Найдите значение выражения:
Слайд 7Исследуйте функцию на чётность и нечётность:
f(x)= x² ·cos²a
Определите знак
Sin100°cos100°
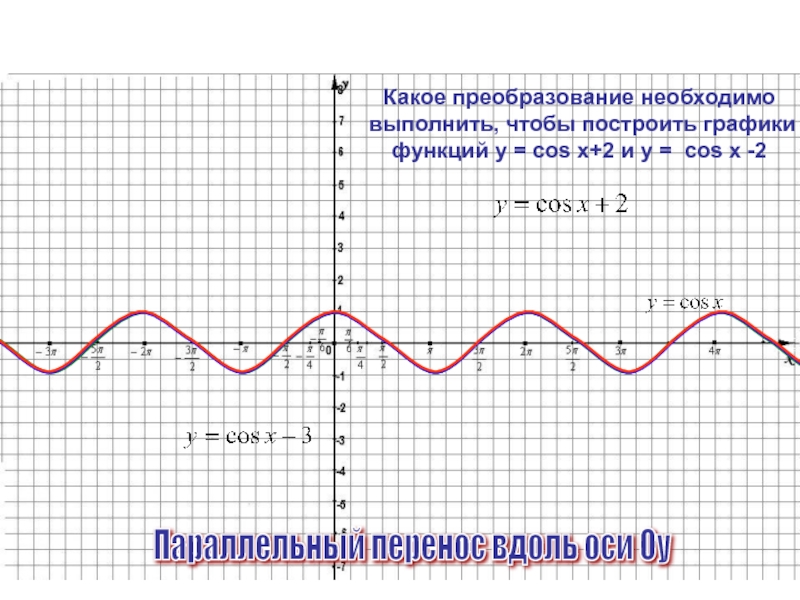
Слайд 8
Параллельный перенос вдоль оси Оу
Какое
выполнить, чтобы построить графики
функций у = cos x+2 и y = cos x -2
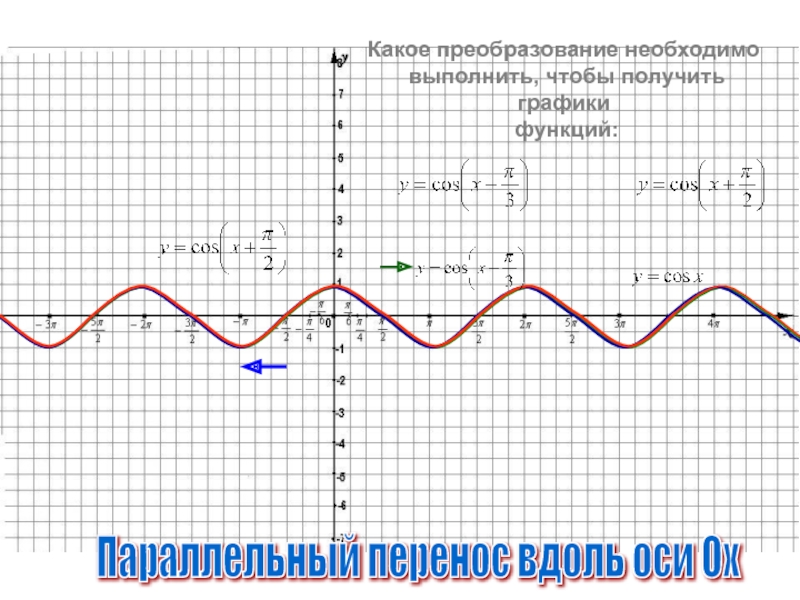
Слайд 9
Параллельный перенос вдоль оси Ох
Какое
выполнить, чтобы получить графики
функций:
Слайд 11Сгруппируйте функции на две группы по какому-нибудь признаку:
y = cos(x + 2); y = cos2x;
y =
y = sin(x – 5); y = cos1/3x; y = 3sinx.
y = cosx + 1; y = – 3cosx; y = 2cosx.
Слайд 12
изменение аргумента
y = cos(x + 2);
y = cos2x; y = sin(x – 5);
y = cos1/3x.
изменение функции
y = sinx + 2;
y =
y = cosx + 1; y = – 3cosx; y = 3sinx.
Слайд 14Для построения графика функции y=kf(x) необходимо график функции y=f(x) растянуть в
y=f(x) → y=kf(x), где k>0
(x0;y0) → (x0;ky0)
Для построения графика функции y=kf(x) необходимо график функции y=f(x) растянуть в k раз вдоль оси ОY для k >1 или сжать в 1/k раз вдоль оси OY для k<1
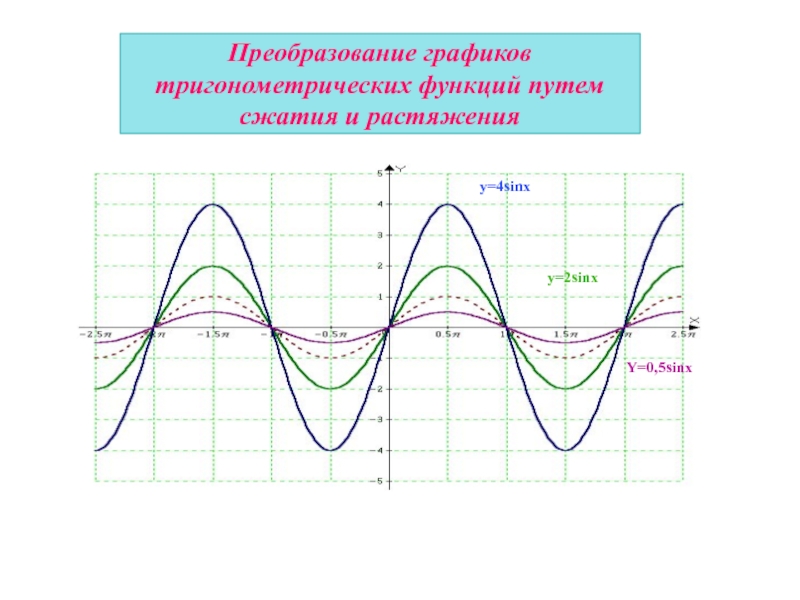
Слайд 15Преобразование графиков тригонометрических функций путем сжатия и растяжения
График функции у =k
График функции у = k f (x) получается из графика функции у = f(x) путем его сжатия в k раз (при 0
Слайд 16Преобразование графиков тригонометрических функций путем сжатия и растяжения
y=2sinx
y=4sinx
Y=0,5sinx
Слайд 24Симметричное отображение относительно оси OY
y=f(x) → y=-f(x)
(x0;y0) →
Для построения графика функции y=-f(x) необходимо график функции y=f(x)симметрично отобразить относительно оси ОХ
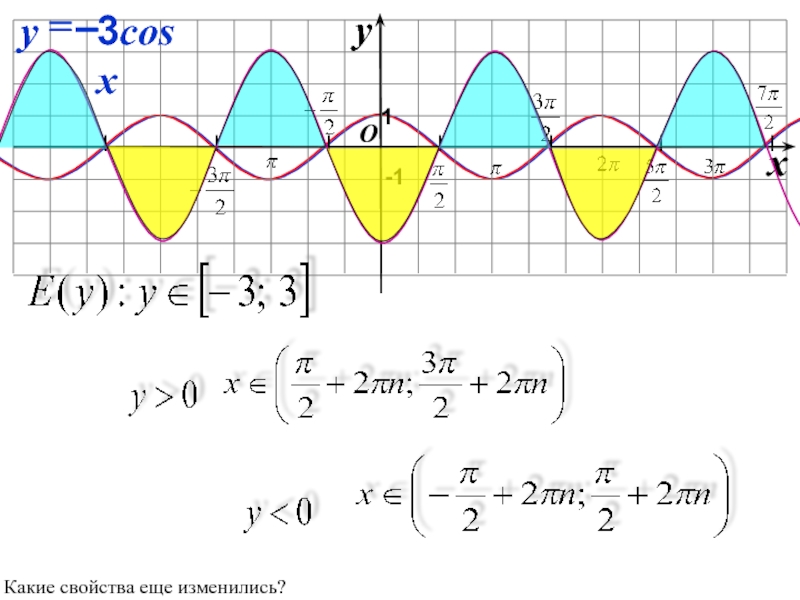
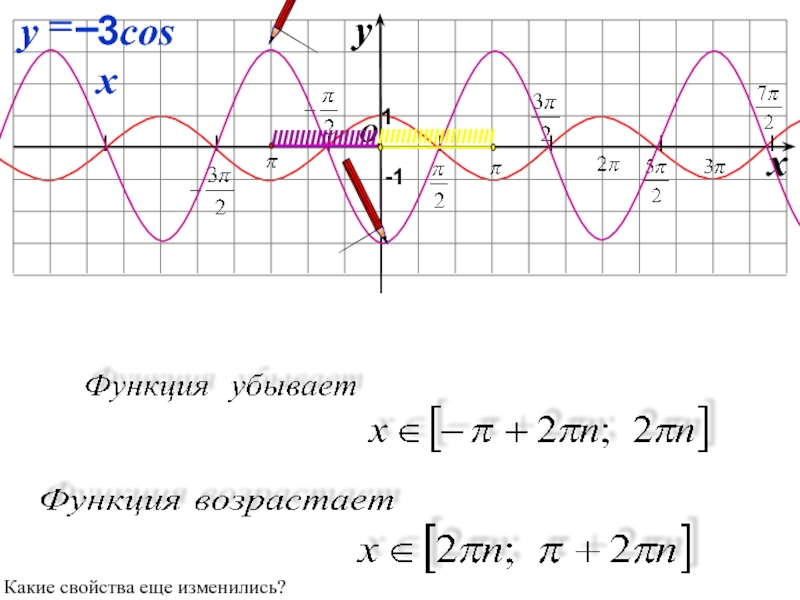
Слайд 26
O
x
y
-1
1
3cos x
=
y
–
Какие свойства еще изменились?
IIIIIIIIIIIIIIIIIII
IIIIIIIIIIIIIIIIIIIII
Слайд 27Итог урока
На данном уроке говорилось о …
Урок мне понравился (не понравился),
Сегодня я понял(а), что…
ИТОГ УРОКА
Слайд 28Домашнее задание.
1.Среди функций выберите те, которые получаются в результате растяжения в
у = 2 sinx; y=sin 2x; y=sin x +2; y =0.5 sin x; y= -3sin(x+П).
2. Среди функций выберите те, которые получаются в результате сжатия в к раз от оси oх:
3. Построить в одной системе координат графики функций:
y = sin x, y = 2 sin x ; y = 0,5 sin x.
4. Решить графически уравнение
cos x = 2x+1
Слайд 29Растяжение (сжатие) в k раз вдоль оси OХ
y=f(x)
(x0;y0) → ( x0;y0)
Для построения графика функции y=f(kx) необходимо график функции y=f(x) сжать в k раз вдоль оси ОХ для k >1 или растянуть в 1/k раз вдоль оси OХ для k<1
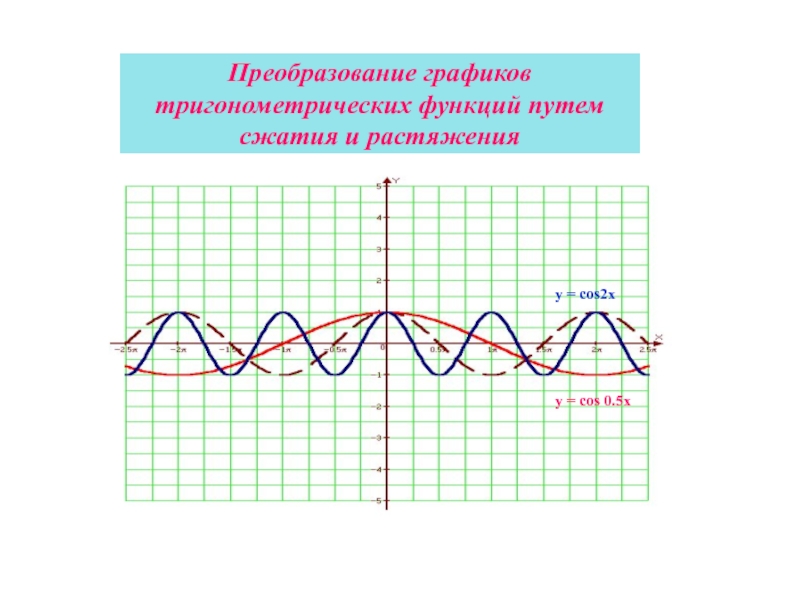
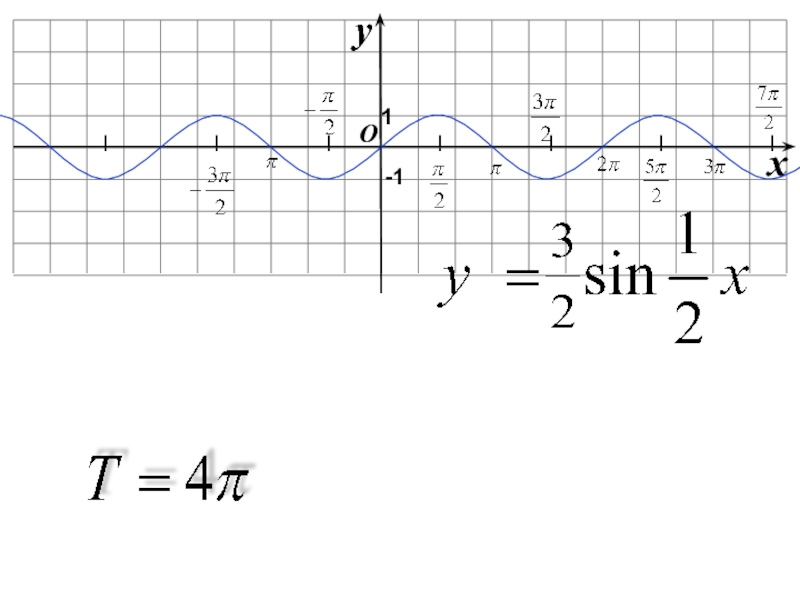
Слайд 30Преобразование графиков тригонометрических функций путем сжатия и растяжения
График функции у =
График функции у = f (kx) получается из графика функции у = f(x) путем его растяжения в k раз (при 0
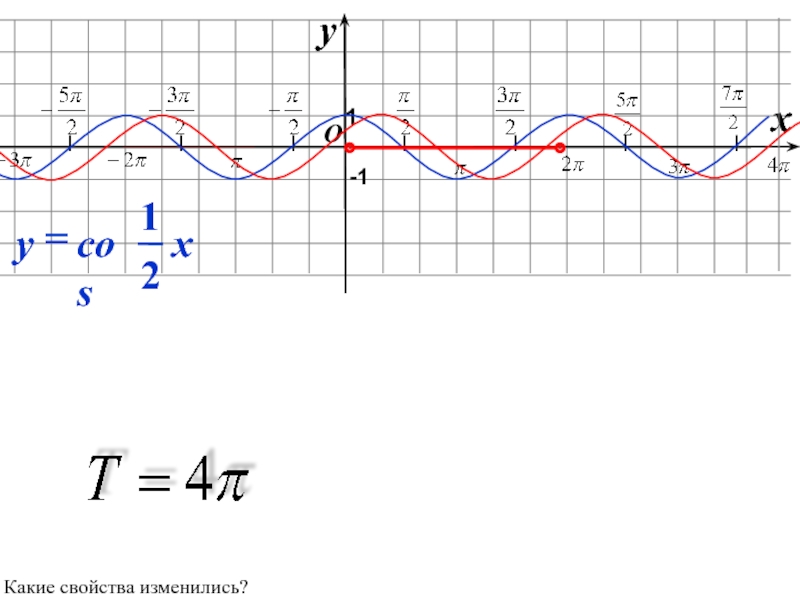
Слайд 31Преобразование графиков тригонометрических функций путем сжатия и растяжения
y = cos2x
y =
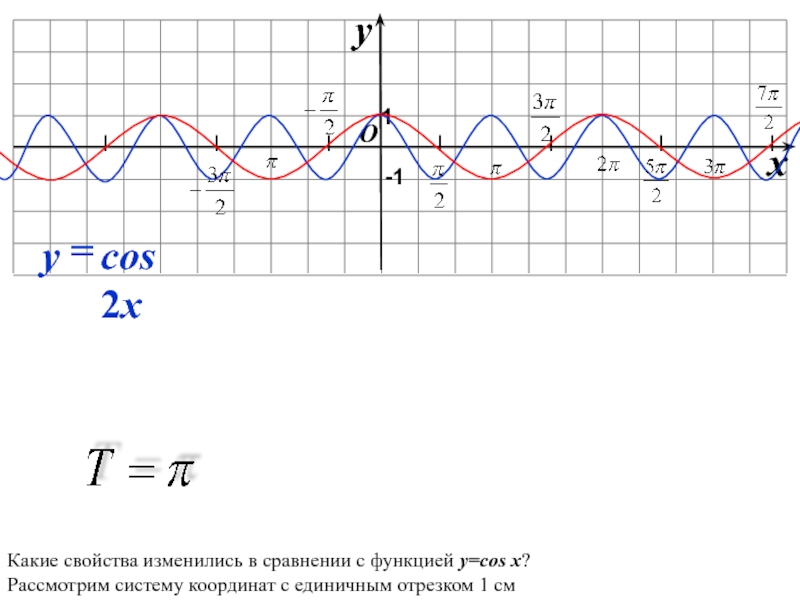
Слайд 33
O
x
y
-1
1
Какие свойства изменились в сравнении с функцией y=cos x?
Рассмотрим систему координат с единичным отрезком 1 см
Слайд 39
O
x
y
-1
1
Какие свойства изменились?
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
Слайд 47Какие преобразования с синусоидой нужно выполнить, чтобы построить график данной функции?
f(x)=0,5cosx
f(x)=3+sinx
f(x)=sin(x-п/4)
f(x)=2cos(x/2+п/3)
Слайд 48ПРИМЕР 3. Построить график функции, заданной формулой
x
y
1
0
Масштаб π:3
−1
Решение. 1) y=sinx;
2)
Слайд 49x
y
1
0
Масштаб π:3
−1
Остается воспользоваться свойством периодичности любой тригонометрической функции (определите наименьший положительный
Слайд 50Для любознательных…
Посмотрите, как выглядят графики некоторых других тригонометрических функций:
y = 1 / cos x или y=sec x
y = cosec x или y= 1/ sin x