Свойства функций
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку алгебры по теме: Функции. Свойства функции.
Содержание
- 1. Презентация к уроку алгебры по теме: Функции. Свойства функции.
- 2. Цели урокасистематизировать знания по теме “Функции и
- 3. Определение функции
- 4. Пример.
- 5. Область определения функции – все значения
- 6. Способы задания функциис помощью формулы:
- 7. График функции - множество точек на координатной
- 8. Функции изученные в школьном курсе математики
- 9. Линейная функция функция вида y = k
- 10. Квадратичная функция функция вида y = x²
- 11. Обратная пропорциональность функция вида y =K/X;
- 12. функция вида y = x³; 1.
- 13. функция вида y =
- 14. Свойства функций возрастание и убывание функцииограниченность функциинаибольшее
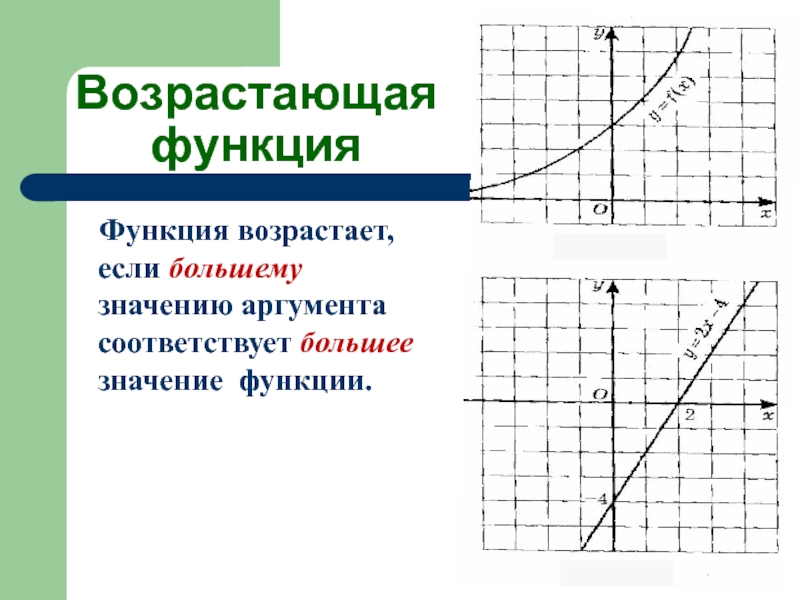
- 15. Возрастающая функция Функция возрастает, если большему значению аргумента соответствует большее значение функции.
- 16. Убывающая функция Функция
- 17. Обычно термины «возрастающая функция», «убывающая
- 18. Определение Функцию у = f(x)
- 19. Определение Функцию у =
- 20. Утверждения:Если у функции существует yнаиб, то
- 21. Определение Точку x0 называют точкой максимума
- 22. Определение Точку x0 называют точкой минимума функции
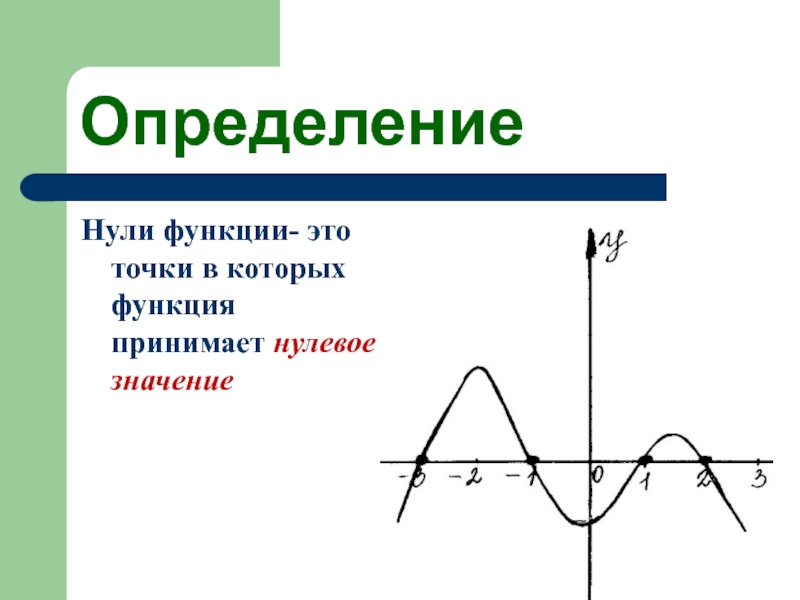
- 23. ОпределениеНули функции- это точки в которых функция принимает нулевое значение
- 24. а) Укажите точки экстремума и определите их вид;б) укажите наибольшее и наименьшее значение функции.-2-2116
- 25. Непрерывность функции Непрерывность
- 26. Слайд 26
- 27. Определение Функцию у = f(x) называют
- 28. Определение Функцию у= f(x) называют
- 29. Алгоритм исследования функции 1. Область определения функции2.
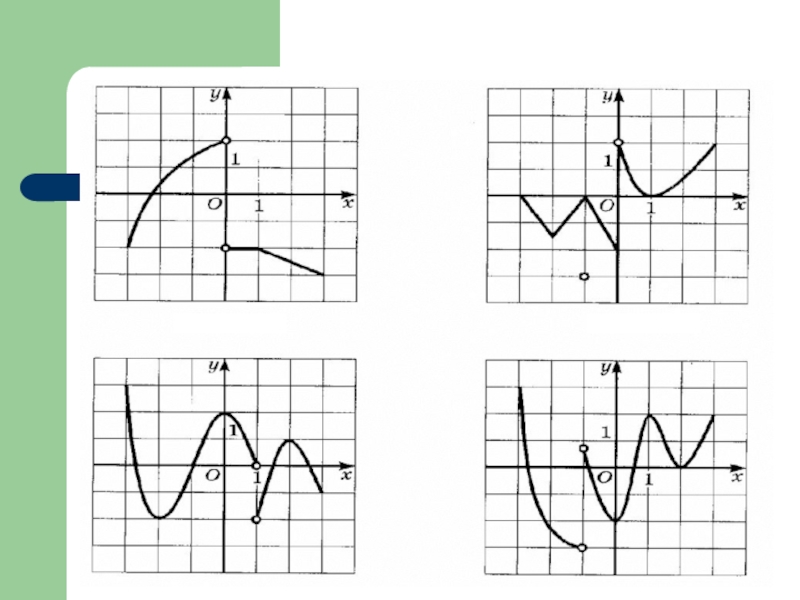
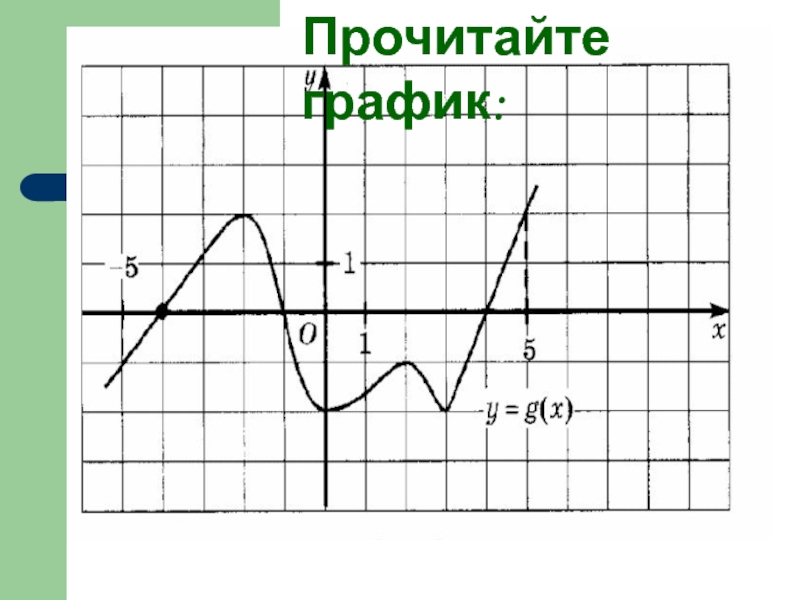
- 30. Прочитайте график:
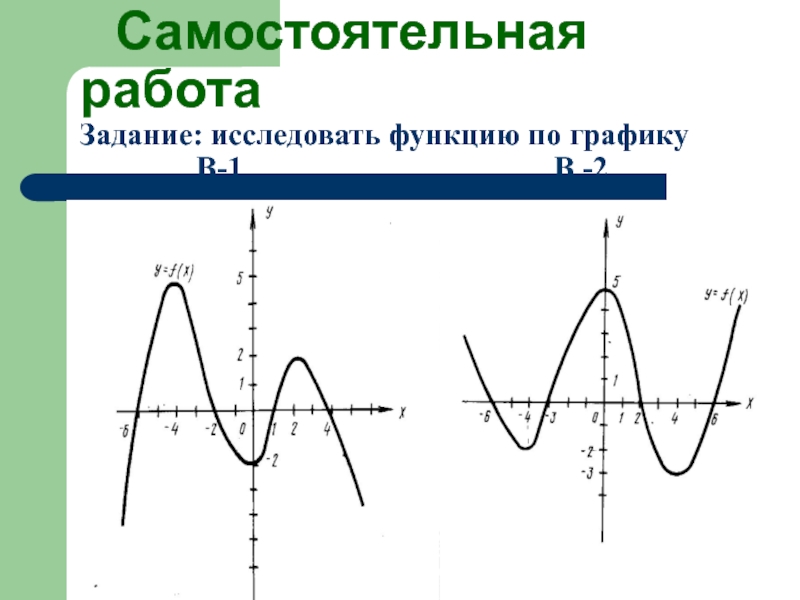
- 31. Самостоятельная работа Задание: исследовать функцию
- 32. В - 1
- 33. Продолжите фразу : Сегодня на уроке я
- 34. Вы молодцы! Каждый из вас «научись тому, что следует знать»
Цели урокасистематизировать знания по теме “Функции и графики” за школьный курс математики;рассмотреть свойства функций: возрастание и убывание, ограниченность, наибольшее и наименьшее значения, максимум и минимум функции, четность и нечетностьнаучиться исследовать функцию по графику
Слайд 2Цели урока
систематизировать знания по теме “Функции и графики” за школьный курс
математики;
рассмотреть свойства функций: возрастание и убывание, ограниченность, наибольшее и наименьшее значения, максимум и минимум функции, четность и нечетность
научиться исследовать функцию по графику
рассмотреть свойства функций: возрастание и убывание, ограниченность, наибольшее и наименьшее значения, максимум и минимум функции, четность и нечетность
научиться исследовать функцию по графику
Слайд 3Определение функции
Функция – это зависимость переменной у от переменной х,
при которой каждому значению переменной х соответствует единственное значение переменной у.
х – независимая переменная или аргумент
у – зависимая переменная или значение функции
Слайд 4Пример.
у = 2х +
3 или f(х) = 2х + 3
Если х = 5, то f(5) = 2 ⋅ 5 + 3=10 + 3 = 13
Если f(х) = 0, то 2х + 3 = 0
2х = -3
х = -1,5
Если х = 5, то f(5) = 2 ⋅ 5 + 3=10 + 3 = 13
Если f(х) = 0, то 2х + 3 = 0
2х = -3
х = -1,5
Если зависимость переменной у от переменной х является функцией, то коротко это записывают так: у = f(х)
Слайд 5
Область определения функции – все значения независимой
переменной х.
Обозначение: D( х )
Область значений функции – все значения зависимой переменной у.
Обозначение: Е( у )
Обозначение: D( х )
Область значений функции – все значения зависимой переменной у.
Обозначение: Е( у )
Слайд 6Способы задания функции
с помощью формулы: y = 2x +
2
с помощью графика:
словесным описанием:
Пусть х – любое число, у(х)- целая часть числа х, т.е. наибольшее целое число, не превосходящее х . Обозначение у(х)=[ х].
с помощью графика:
словесным описанием:
Пусть х – любое число, у(х)- целая часть числа х, т.е. наибольшее целое число, не превосходящее х . Обозначение у(х)=[ х].
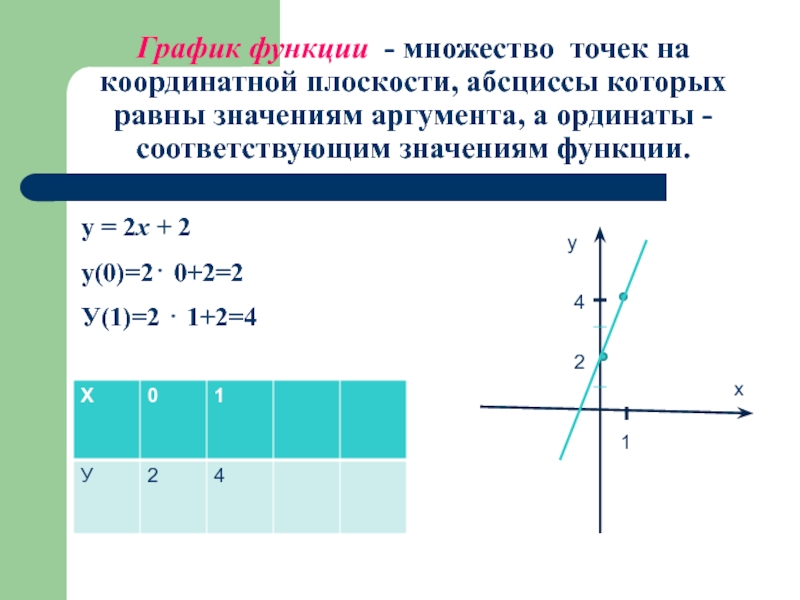
Слайд 7График функции - множество точек на координатной плоскости, абсциссы которых равны
значениям аргумента, а ординаты - соответствующим значениям функции.
y = 2x + 2
у(0)=2⋅ 0+2=2
У(1)=2 ⋅ 1+2=4
у
х
4
2
1
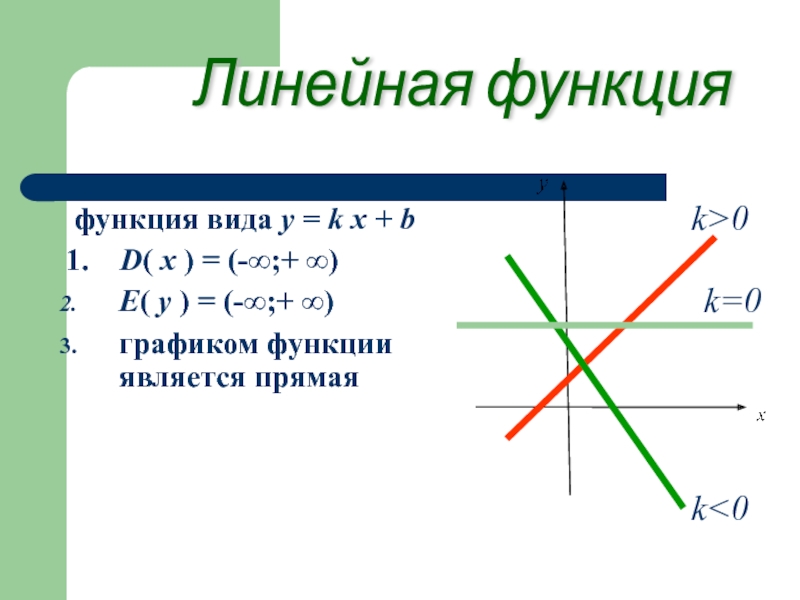
Слайд 9Линейная функция
функция вида y = k х + b
1.
D( х ) = (-∞;+ ∞)
E( у ) = (-∞;+ ∞)
графиком функции является прямая
E( у ) = (-∞;+ ∞)
графиком функции является прямая
k>0
k<0
k=0
Слайд 10Квадратичная функция
функция вида y = x²
1. D( х
) = (-∞;+ ∞)
2. E( у ) = = [0;∞);
3. графиком функции является парабола
2. E( у ) = = [0;∞);
3. графиком функции является парабола
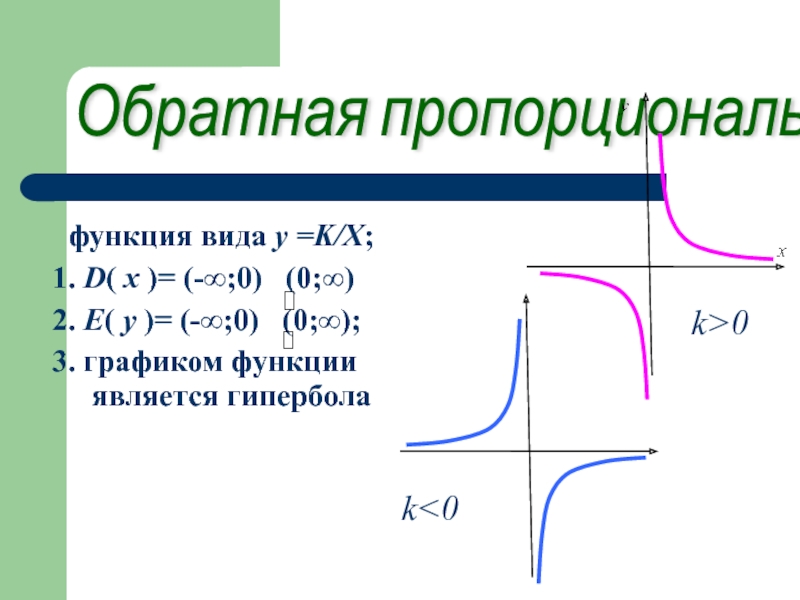
Слайд 11Обратная пропорциональность
функция вида y =K/X;
1. D( х )=
(-∞;0) (0;∞)
2. E( у )= (-∞;0) (0;∞);
3. графиком функции является гипербола
2. E( у )= (-∞;0) (0;∞);
3. графиком функции является гипербола
k>0
k<0
Слайд 12 функция вида y = x³;
1. D( х ) =
(-∞;+ ∞)
2. E( у ) = (-∞;+ ∞)
3. графиком функции является кубическая парабола
2. E( у ) = (-∞;+ ∞)
3. графиком функции является кубическая парабола
Кубическая функция
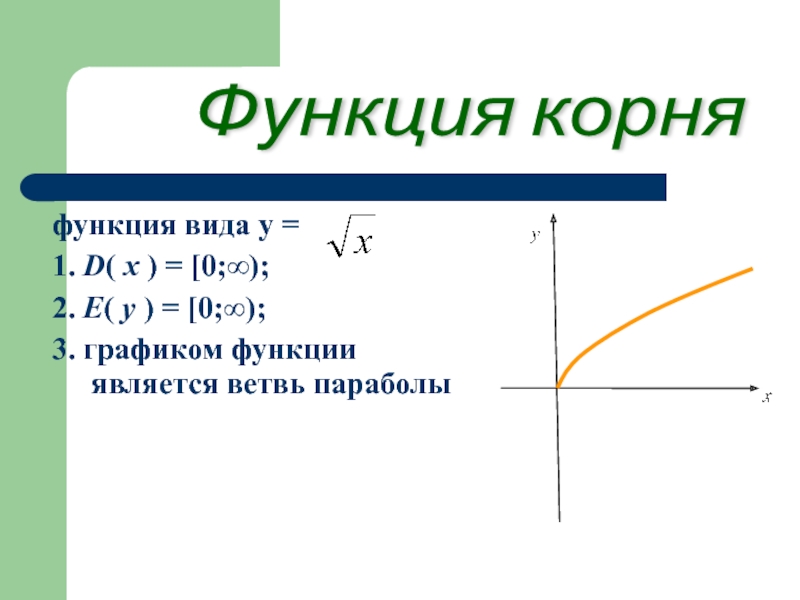
Слайд 13функция вида y =
1. D( х )
= [0;∞);
2. E( у ) = [0;∞);
3. графиком функции является ветвь параболы
2. E( у ) = [0;∞);
3. графиком функции является ветвь параболы
Функция корня
Слайд 14Свойства функций
возрастание и убывание функции
ограниченность функции
наибольшее и наименьшее значения функции
максимум
и минимум функции
четность и нечетность
четность и нечетность
Слайд 15Возрастающая функция
Функция возрастает, если большему значению аргумента соответствует
большее значение функции.
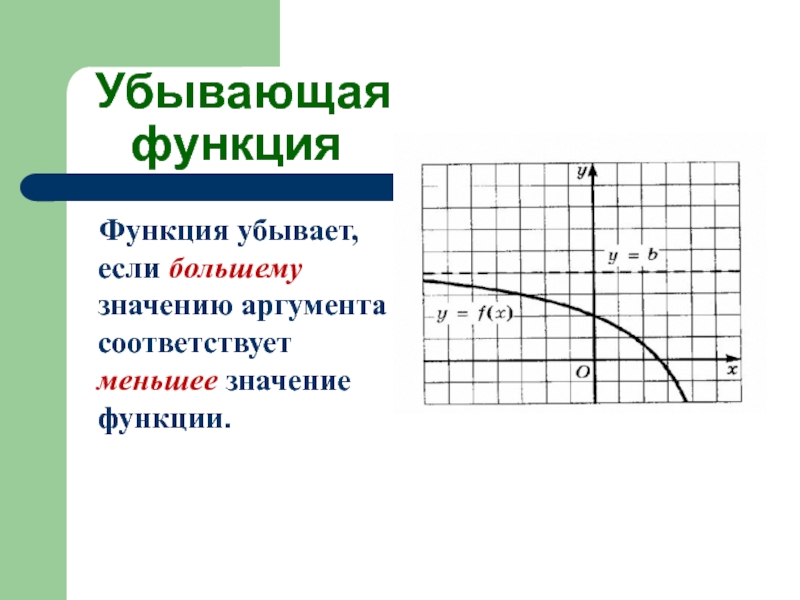
Слайд 16 Убывающая
функция
Функция убывает, если большему значению аргумента
соответствует меньшее значение функции.
Слайд 17 Обычно термины «возрастающая функция», «убывающая функция» объединяют общим названием
монотонная функция, а исследование функции на возрастание или убывание называют исследованием функции на монотонность.
Слайд 18Определение
Функцию у = f(x) называют ограниченной снизу на
множестве Х, если все значения этой функции на множестве Х больше некоторого числа, т.е., если существует такое число m, что для любого значения х выполняется неравенство f(x) > m
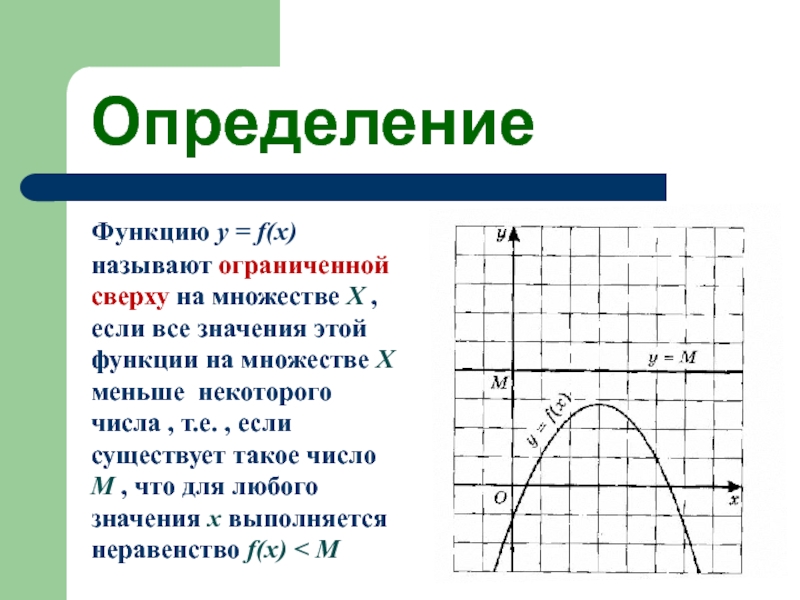
Слайд 19 Определение
Функцию у = f(x) называют ограниченной сверху
на множестве Х , если все значения этой функции на множестве Х меньше некоторого числа , т.е. , если существует такое число М , что для любого значения х выполняется неравенство f(x) < М
Слайд 20Утверждения:
Если у функции существует yнаиб,
то она ограничена сверху
Если у
функции существует yнаим, то она ограничена снизу
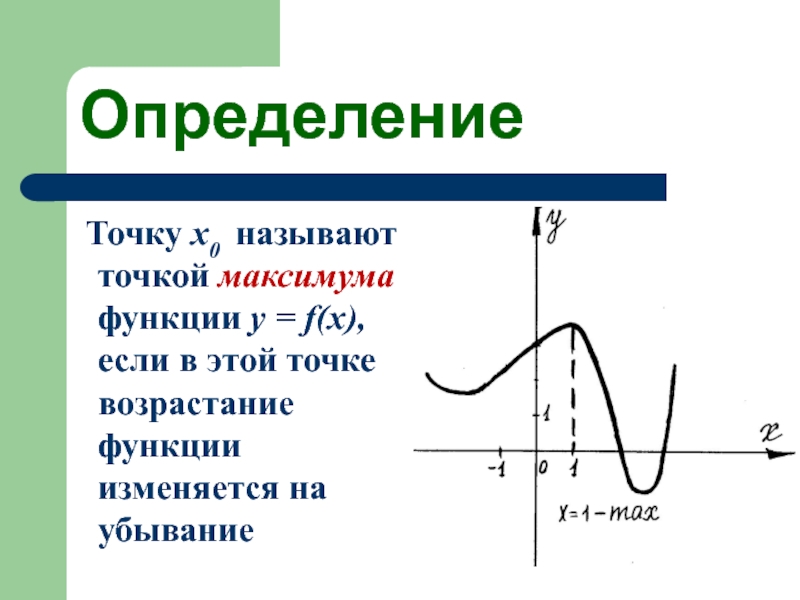
Слайд 21Определение
Точку x0 называют точкой максимума функции у = f(x),
если в этой точке возрастание функции изменяется на убывание
Слайд 22Определение
Точку x0 называют точкой минимума функции у= f(x), если в
этой точке убывание функции изменяется на возрастание
Точки максимума и минимума объединяют общим названием – точки экстремума
Точки максимума и минимума объединяют общим названием – точки экстремума
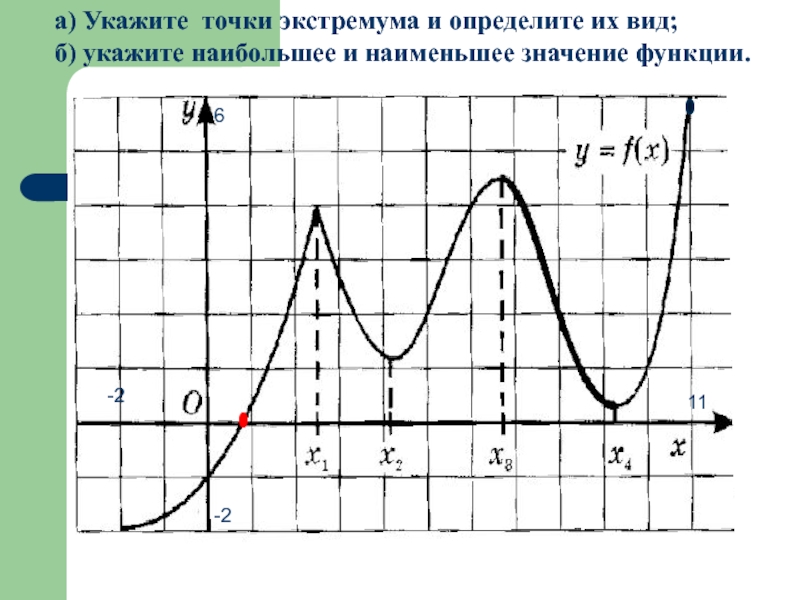
Слайд 24а) Укажите точки экстремума и определите их вид;
б) укажите наибольшее и
наименьшее значение функции.
-2
-2
11
6
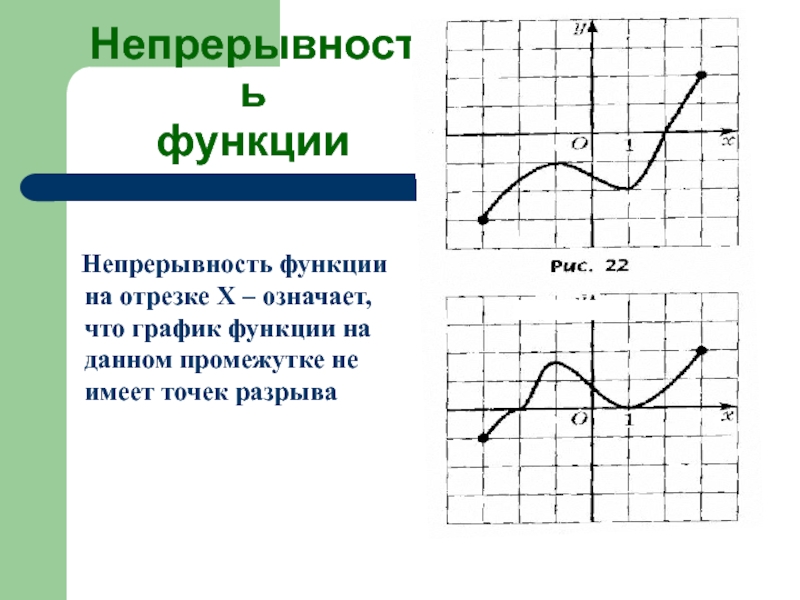
Слайд 25Непрерывность
функции
Непрерывность функции на отрезке Х
– означает, что график функции на данном промежутке не имеет точек разрыва
Слайд 27Определение
Функцию у = f(x) называют четной, если для
любого значения х из множества Х выполняется равенство
Утверждение
Если график функции симметричен относительно оси ординат, то функция четная
Утверждение
Если график функции симметричен относительно оси ординат, то функция четная
Слайд 28Определение
Функцию у= f(x) называют нечетной, если для любого
значения х из множества Х выполняется равенство
Утверждение
Если график функции симметричен относительно начала координат, то функция нечетная
Утверждение
Если график функции симметричен относительно начала координат, то функция нечетная
Слайд 29Алгоритм исследования функции
1. Область определения функции
2. Множество значений функции
3. Четность
, нечетность
4. Непрерывность
5. Нули функции
6. Промежутки возрастания и убывания
7. Точки экстремума
8. Ограниченность функции
9. Наибольшее и наименьшее значения функции
4. Непрерывность
5. Нули функции
6. Промежутки возрастания и убывания
7. Точки экстремума
8. Ограниченность функции
9. Наибольшее и наименьшее значения функции
Слайд 32 В - 1
В - 2
1. D( х )=(-∞;+ ∞)
2. Е (у) =(-∞;5]
3. ни четная, ни не четная
4. непрерывная
5. х=- 5, х= -2, х=1, х=4
6. Возрастает на (-∞;-4)∪(0;2)
Убывает на (-4;0)∪(2;+ ∞)
7. х=- 4, х=2 - max
х=0 - min
8. Ограниченная у=5
9. Наибольшее у=5,
наименьшее - нет
1. D( х )=(-∞;+ ∞)
2. Е (у) = [-3;-∞)
3. ни четная, ни не четная
4. непрерывная
5. х= -6, х= -3, х= 2, х= 6
6. Возрастает на (-4;0)∪(4;+ ∞)
Убывает на (-∞;-4)∪(0;4)
7. х= -4, х= 4 - min
х= 0 - max
8. Ограниченная у= -3
9. Наибольшее - нет
наименьшее у= - 3
Слайд 33Продолжите фразу :
Сегодня на уроке я повторил …
Сегодня на уроке я
узнал …
Сегодня на уроке я научился …
Сегодня на уроке я научился …
