- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку алгебры на тему Случайные события (9 класс)
Содержание
- 1. Презентация к уроку алгебры на тему Случайные события (9 класс)
- 2. Теория вероятностей – это раздел математики, который
- 3. Методы теории вероятностей широко применяются в различных
- 4. СобытияСлучайное событие - это событие, которое в
- 5. В корзине лежало 3 красных и 3
- 6. Три господина, придя в ресторан, сдали в
- 7. СобытияСовместные события – это события, которые в
- 8. Слайд 8
- 9. Слайд 9
- 10. Вероятность событияИзмерение степени достоверности наступления какого-либо события?Блез Паскаль (1623-1662)Пьер Ферма (1601-1665)
- 11. Вероятность - доля успеха того или иного событияР – вероятность, от латинского слова probabilitas
- 12. Правило произведения. Если существует n вариантов выбора
- 13. Правило произведения. Если существует n вариантов выбора
- 14. Правило произведения. Если существует n вариантов выбора
- 15. Правило произведения. Если существует n вариантов выбора
- 16. Задача. В ящике имеется три одинаковых по
Слайд 1Случайные события
Основные вопросы:
Понятие «теория вероятностей»
Классификация событий
Вероятность события
Решение задач
Учитель математики: Денисова Ю.А.
СПб
Слайд 2Теория вероятностей – это раздел математики, который занимается изучением математических моделей
Слайд 3Методы теории вероятностей широко применяются в различных отраслях естествознания и техники:
теории массового обслуживания,
теоретической физике,
геодезии,
астрономии,
теории стрельбы,
теории ошибок наблюдений,
теории автоматического управления,
общей теории связи и во многих других теоретических и прикладных науках.
Теория вероятностей служит также для обоснования математической и прикладной статистики, которая в свою очередь используется при планировании и организации производства, при анализе технологических процессов, предупредительном и приемочном контроле качества продукции и для многих других целей.
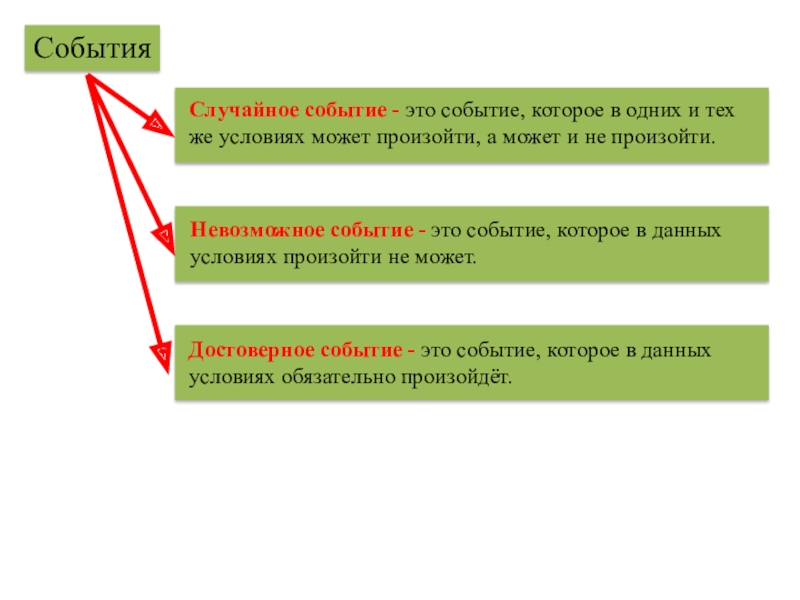
Слайд 4События
Случайное событие - это событие, которое в одних и тех же
Невозможное событие - это событие, которое в данных условиях произойти не может.
Достоверное событие - это событие, которое в данных условиях обязательно произойдёт.
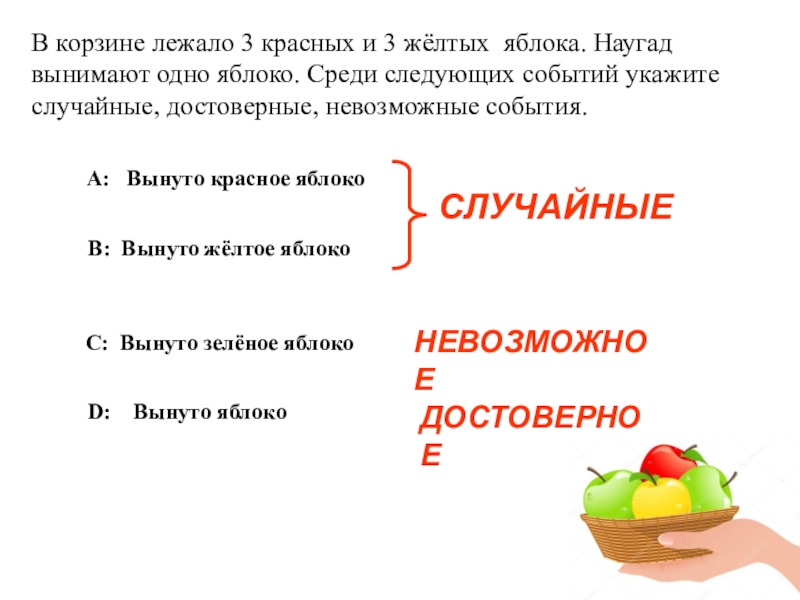
Слайд 5В корзине лежало 3 красных и 3 жёлтых яблока. Наугад вынимают
А: Вынуто красное яблоко
В: Вынуто жёлтое яблоко
С: Вынуто зелёное яблоко
D: Вынуто яблоко
СЛУЧАЙНЫЕ
НЕВОЗМОЖНОЕ
ДОСТОВЕРНОЕ
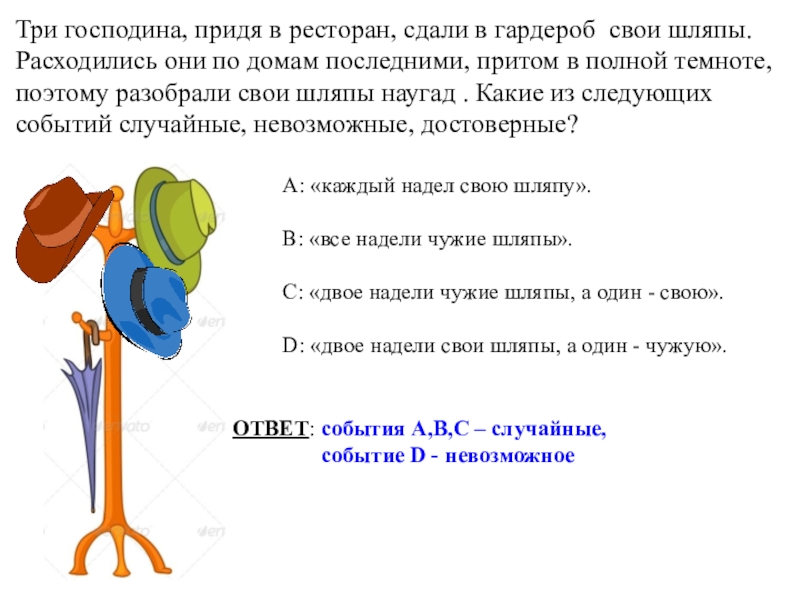
Слайд 6Три господина, придя в ресторан, сдали в гардероб свои шляпы.
Расходились
поэтому разобрали свои шляпы наугад . Какие из следующих событий случайные, невозможные, достоверные?
А: «каждый надел свою шляпу».
В: «все надели чужие шляпы».
С: «двое надели чужие шляпы, а один - свою».
D: «двое надели свои шляпы, а один - чужую».
ОТВЕТ: события А,В,С – случайные,
событие D - невозможное
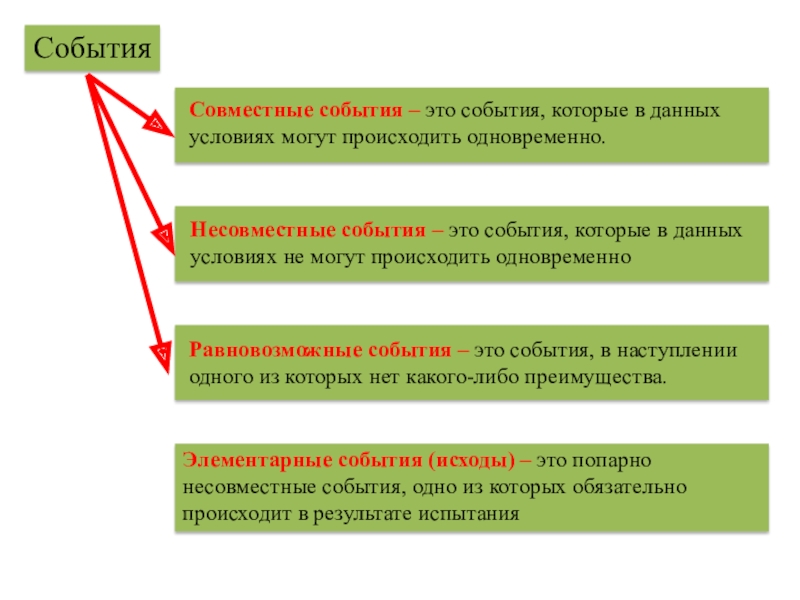
Слайд 7События
Совместные события – это события, которые в данных условиях могут происходить
Несовместные события – это события, которые в данных условиях не могут происходить одновременно
Равновозможные события – это события, в наступлении одного из которых нет какого-либо преимущества.
Элементарные события (исходы) – это попарно несовместные события, одно из которых обязательно происходит в результате испытания
Слайд 10Вероятность события
Измерение степени достоверности наступления какого-либо события?
Блез Паскаль (1623-1662)
Пьер Ферма (1601-1665)
Слайд 11Вероятность - доля успеха того или иного события
Р – вероятность, от
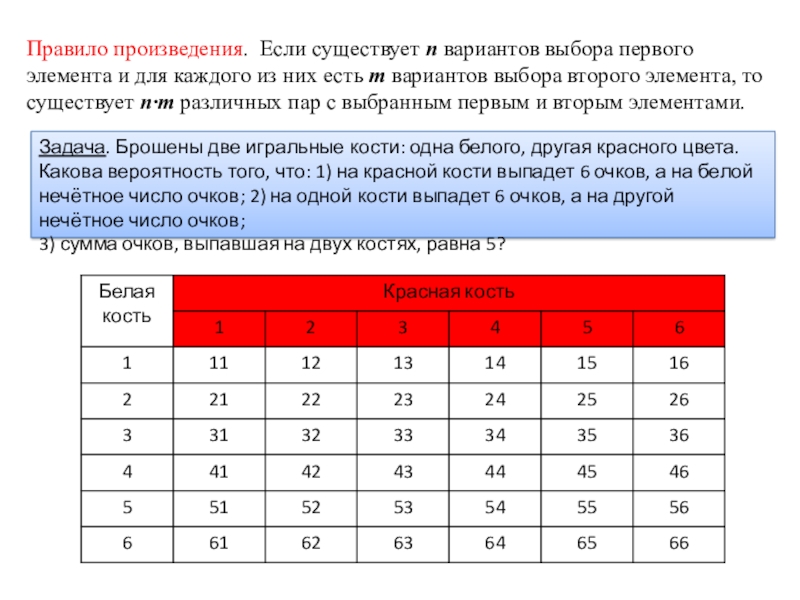
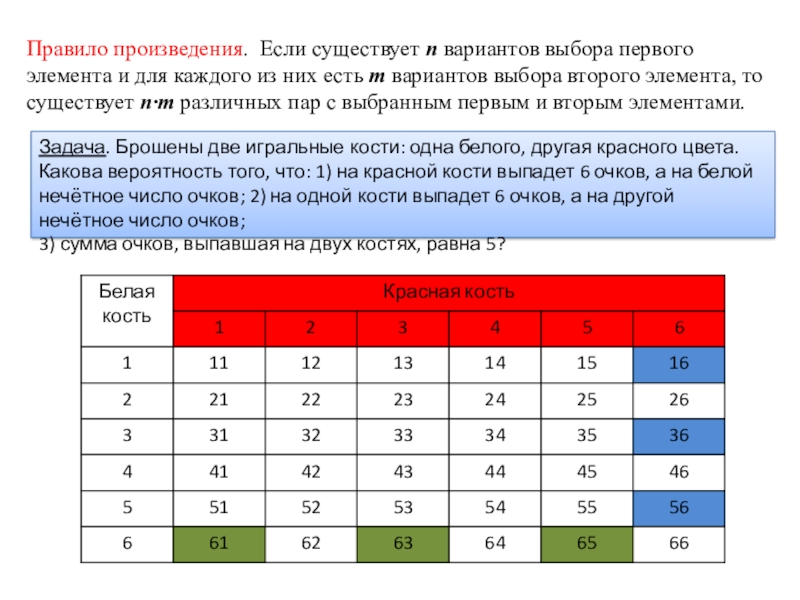
Слайд 12Правило произведения. Если существует n вариантов выбора первого элемента и для
Задача. Брошены две игральные кости: одна белого, другая красного цвета. Какова вероятность того, что: 1) на красной кости выпадет 6 очков, а на белой нечётное число очков; 2) на одной кости выпадет 6 очков, а на другой нечётное число очков;
3) сумма очков, выпавшая на двух костях, равна 5?
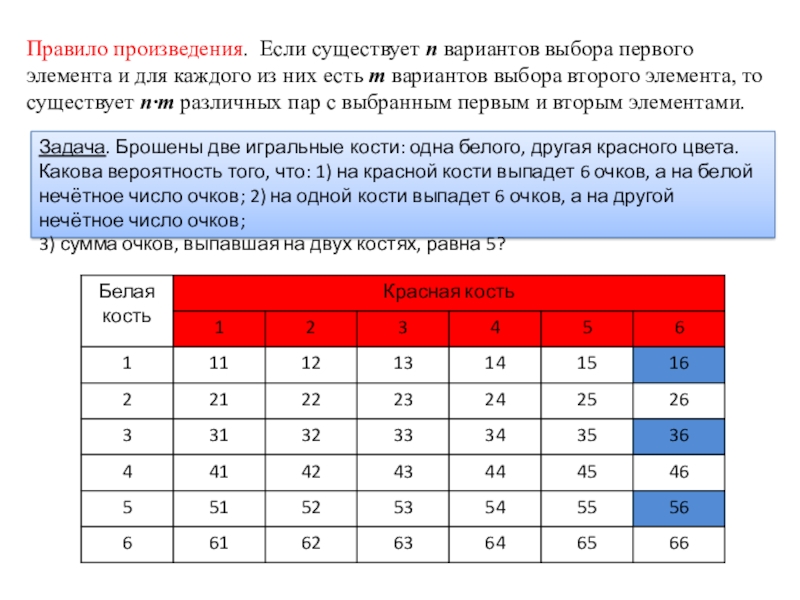
Слайд 13Правило произведения. Если существует n вариантов выбора первого элемента и для
Задача. Брошены две игральные кости: одна белого, другая красного цвета. Какова вероятность того, что: 1) на красной кости выпадет 6 очков, а на белой нечётное число очков; 2) на одной кости выпадет 6 очков, а на другой нечётное число очков;
3) сумма очков, выпавшая на двух костях, равна 5?
Слайд 14Правило произведения. Если существует n вариантов выбора первого элемента и для
Задача. Брошены две игральные кости: одна белого, другая красного цвета. Какова вероятность того, что: 1) на красной кости выпадет 6 очков, а на белой нечётное число очков; 2) на одной кости выпадет 6 очков, а на другой нечётное число очков;
3) сумма очков, выпавшая на двух костях, равна 5?
Слайд 15Правило произведения. Если существует n вариантов выбора первого элемента и для
Задача. Брошены две игральные кости: одна белого, другая красного цвета. Какова вероятность того, что: 1) на красной кости выпадет 6 очков, а на белой нечётное число очков; 2) на одной кости выпадет 6 очков, а на другой нечётное число очков;
3) сумма очков, выпавшая на двух костях, равна 5?
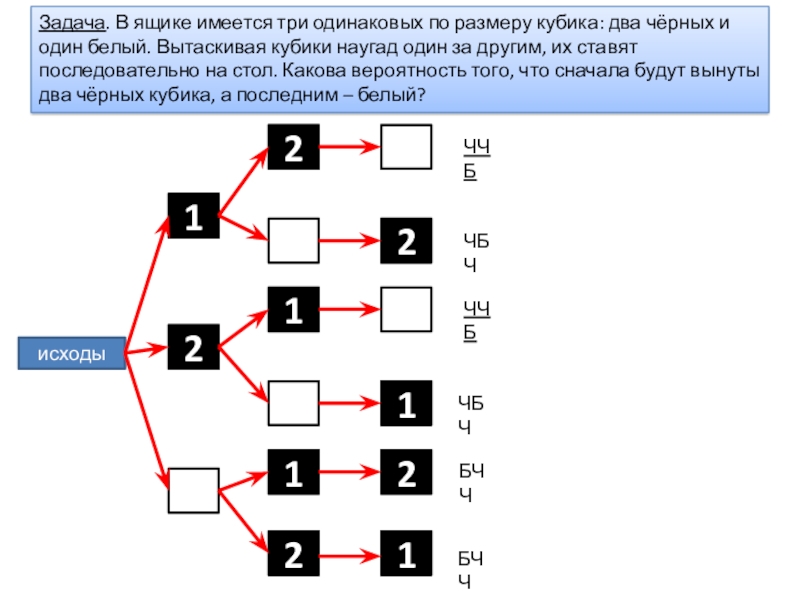
Слайд 16Задача. В ящике имеется три одинаковых по размеру кубика: два чёрных
исходы
1
2
1
2
2
1
1
2
1
2
ЧЧБ
ЧБЧ
ЧЧБ
ЧБЧ
БЧЧ
БЧЧ