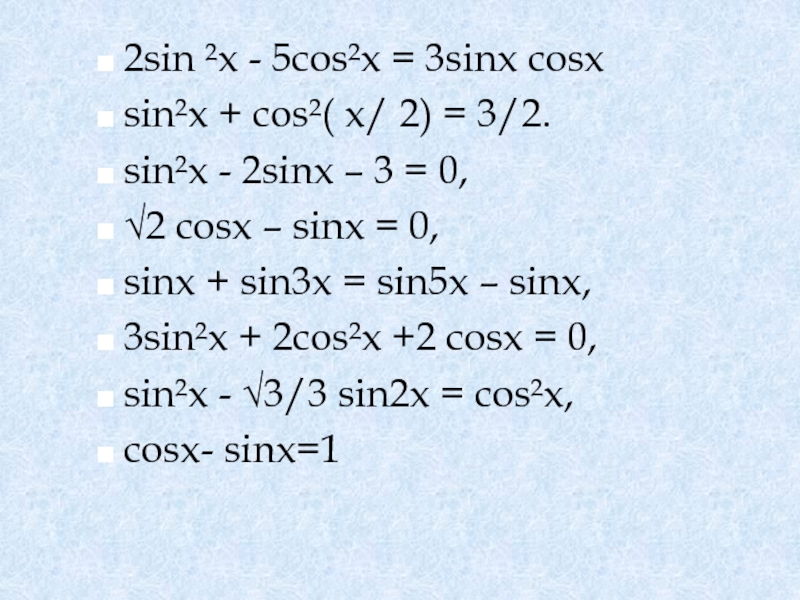- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку алгебры и начал анализа по теме Тригонометрические уравнения и неравенства
Содержание
- 1. Презентация к уроку алгебры и начал анализа по теме Тригонометрические уравнения и неравенства
- 2. Решение тригонометрических уравнений и неравенств (10 класс)
- 3. Проверочная работа.Каково будет решение уравнения cos x
- 4. Проверочная работа.5. В каком промежутке находится
- 5. Проверочная работа.9. Каким будет решение
- 6. Слайд 6
- 7. Методы решения тригонометрических уравнений.Разложение на множителиУравнения сводимые
- 8. Среди уравнений, данных на слайде, выбрать те,
- 9. 2sin ²x - 5cos²x = 3sinx cosxsin²x
- 10. Приведением к квадратному и заменой переменной решаются
- 11. Делением на старшую степень решаются уравнения. 2sin
- 12. Делением на старшую степень решаются уравнения.√2 cosx
- 13. Понижение степени используют при решении уравнения. sin²x
- 14. С помощью формул суммы или разности решаются
- 15. Делением на старшую степень решаются уравнения.sin²x -
- 16. Решение последнего уравненияпредлагается выполнить по группам
- 17. Алгоритм решения тригонометрического неравенства:1. Отметить на оси абсцисс
- 18. Решение неравенствРеши неравенства:Проверь ответы:
- 19. Проверь решения неравенств2) sin х ≥0-π/6 +2πk
- 20. Подведение итоговИтак, мы повторили материал очень важной
- 21. Молодцы!
Слайд 2Решение тригонометрических уравнений и неравенств (10 класс) учитель МбОУ гимназии №30 города Ставрополя ивженко
Слайд 3Проверочная работа.
Каково будет решение
уравнения cos x = a при
Каково будет решение
уравнения sin x = a при а > 1
2. При каком значении а
уравнение cos x = a имеет
решение?
При каком значении а
уравнение sin x = a имеет
решение?
Какой формулой
выражается это решение?
Какой формулой
выражается это решение?
4.
На какой оси откладывается
значение а при решении
уравнения cos x = a ?
4.
На какой оси откладывается
значение а при решении
уравнения sin x = a ?
Слайд 4Проверочная работа.
5. В каком промежутке
находится arccos a ?
5.
находится arcsin a ?
В каком промежутке
находится значение а?
6. В каком промежутке
находится значение а?
Каким будет решение
уравнения cos x = 1?
7. Каким будет решение
уравнения sin x = 1?
8. Каким будет решение
уравнения cos x = -1?
8. Каким будет решение
уравнения sin x = -1?
Слайд 5Проверочная работа.
9. Каким будет решение
уравнения cos x
9. Каким будет решение
уравнения sin x = 0?
Чему равняется
arccos ( - a)?
10. Чему равняется
arcsin ( - a)?
В каком промежутке
находится arctg a?
11. В каком промежутке
находится arcctg a?
Какой формулой
выражается решение
уравнения tg x = а?
12. Какой формулой
выражается решение
уравнения сtg x = а?
Слайд 7Методы решения
тригонометрических уравнений.
Разложение на множители
Уравнения сводимые
к алгебраическим
Введение новой переменной
(однородные уравнения)
Введение
аргумента.
Уравнения, решаемые переводом
суммы в произведение
Слайд 8Среди уравнений, данных на слайде, выбрать те, которые решаются
Заменой переменной;
Приведением
Делением на старшую степень синуса или косинуса, т. е. как однородные;
Понижением степени;
С помощью формул суммы или разности;
Методом вспомогательного аргумента.
Слайд 92sin ²x - 5cos²x = 3sinx cosx
sin²x + cos²( x/ 2)
sin²x - 2sinx – 3 = 0,
√2 cosx – sinx = 0,
sinx + sin3x = sin5x – sinx,
3sin²x + 2cos²x +2 cosx = 0,
sin²x - √3/3 sin2x = cos²x,
cosx- sinx=1
Слайд 10Приведением к квадратному и заменой переменной решаются уравнения.
sin²x - 2sinx –
пусть sinx = t,
тогда t²+ 2 t – 3 = 0,
где t = -3; 1.
Учитывая, что
lsinхl≤1,
а -3<-1,
имеем sinx = 1,
Х =¶ /2+2¶n, n Є Z.
Ответ: ¶ /2+2¶n, n Є Z.
3sin²x + 2cos²x +2 cosx = 0
sin²x = 1 - cos²x,
значит,
3 - 3cos²x + 2cos²x +2cosx = 0,
cos²x - 2cosx – 3 = 0,
пусть cosx = t,
тогда t²- 2 t – 3 = 0,
где t = 3; -1
3>1, ЗНАЧИТ,
cosx = -1,
Х = ¶ + 2¶n, n Є Z.
Ответ: ¶ + 2¶n, n Є Z.
Слайд 11Делением на старшую степень решаются уравнения.
2sin ²x - 5cos²x =
Разделив каждое слагаемое на cos²x,получим.
2tg²х - 3tgх - 5 = 0,
Пусть tgх = p, тогда 2p² - 3p - 5 = 0, где p = 2,5; -1,
tgх =2,5, х = arctg2,5 + ¶n, n Є Z;
tgх = -1, х =¶/4 +¶n, n Є Z.
Ответ: arctg2,5 + ¶n, n Є Z; ¶/4 +¶n, n Є Z.
Слайд 12Делением на старшую степень решаются уравнения.
√2 cosx – sinx = 0
tgх = √2, х = arctg√2 + ¶n, n Є Z
ответ: arctg√2 + ¶n, n Є Z
Слайд 13Понижение степени используют при решении уравнения.
sin²x + cos²( x/ 2)
sin²x + ½(1 +cosx) =3/2,
2 sin²x + 1 +cosx -3 = 0,
2 - 2 cos²x + 1 +cosx -3 = 0,
2 cos²x - cosx = 0,
cosx(2 cosx – 1) = 0,
cosx = 0 или cosx =1/2
Х = ¶/2 + ¶n, n Є Z или Х = ±¶/3 + 2¶n, n Є Z.
Ответ: ±¶/3 + 2¶n, n Є Z; ¶/2 + ¶n, n Є Z.
Слайд 14С помощью формул суммы или разности решаются уравнения.
sinx + sin3x
2 sin2x cosx - 2 sin2x cos3x = 0,
sin2x (cosx - cos3x) = 0,
sin²2x sinx = 0,
sin2x = 0 или sinx = 0,
Х = ¶/2 n, n Є Z или Х = ¶n, n Є Z.
Объединив множества,
получим, Х = ¶/2 n, n Є Z
Ответ: ¶/2 n, n Є Z
Слайд 15Делением на старшую степень решаются уравнения.
sin²x - √3/ 3sin2x = cos²x
tg²х - √3/3 tg x- 1=0,
tgх = √3/6(1 ± √13),
х = arctg √3/6(1 ± √13)+ ¶n, n Є Z;
ответ: arctg √3/6(1 ± √13)+ ¶n, n Є Z
Слайд 16 Решение последнего уравнения
предлагается выполнить по группам различными методами:
cosx- sinx=1.
-приведение к
-разложение на множители(2группа) ;
-введение вспомогательного угла(3группа) ;
-преобразование разности в произведение(4группа)
Слайд 17Алгоритм решения тригонометрического неравенства:
1. Отметить на оси абсцисс интервал
2. Выделить дугу окружности,
3. Выбрать положительный обход дуги (против часовой стрелки)
4. Записать числовые значения точек t1 и t2 , учитывая, что начало дуги – меньшее значение
5. Записать общее решение неравенства
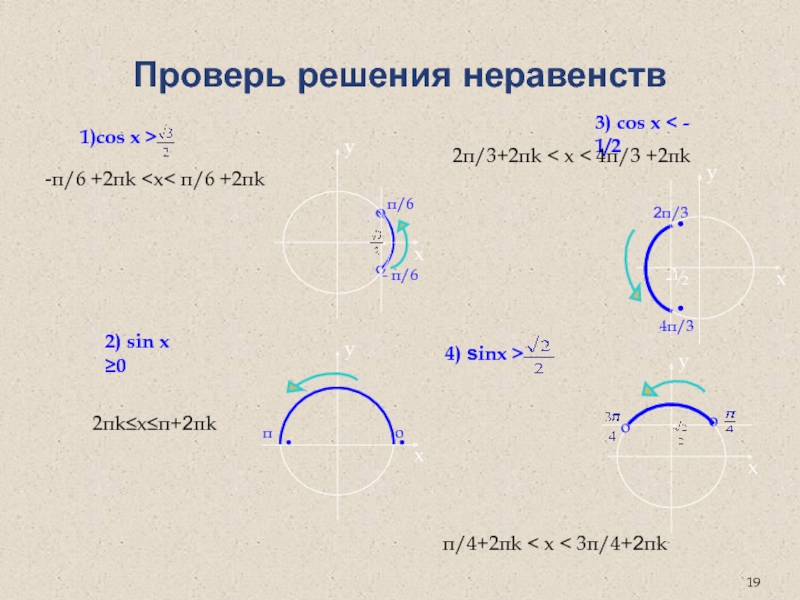
Слайд 19Проверь решения неравенств
2) sin х ≥0
-π/6 +2πk
2π/3+2πk < х < 4π/3 +2πk
π/4+2πk < х < 3π/4+2πk
Слайд 20Подведение итогов
Итак, мы повторили материал очень важной темы
« Тригонометрические уравнения
Сегодня на уроке вспомнили общие формулы решений простейших тригонометрических уравнений, а также частные формулы, алгоритм решения тригонометрических неравенств.
На уроке также были рассмотрены основные виды и способы решения тригонометрических уравнений:
разложение на множители;
замена переменной;
однородные тригонометрические уравнения 1-й и 2-й степени.