- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку алгебры 8 класс по теме Функция у = √х, ее свойства и график
Содержание
- 1. Презентация к уроку алгебры 8 класс по теме Функция у = √х, ее свойства и график
- 2. Цели:
- 3. Внимание!Независимая переменная х имеет степень не выше
- 4. Слайд 4
- 5. у = х²(0; 0), (1; 1), (2;
- 6. у = -х²у = - х²,
- 7. Рассмотрим функциюВспомним! 1. Область определения функции (-∞; +∞).2. у=0 при х=0; у
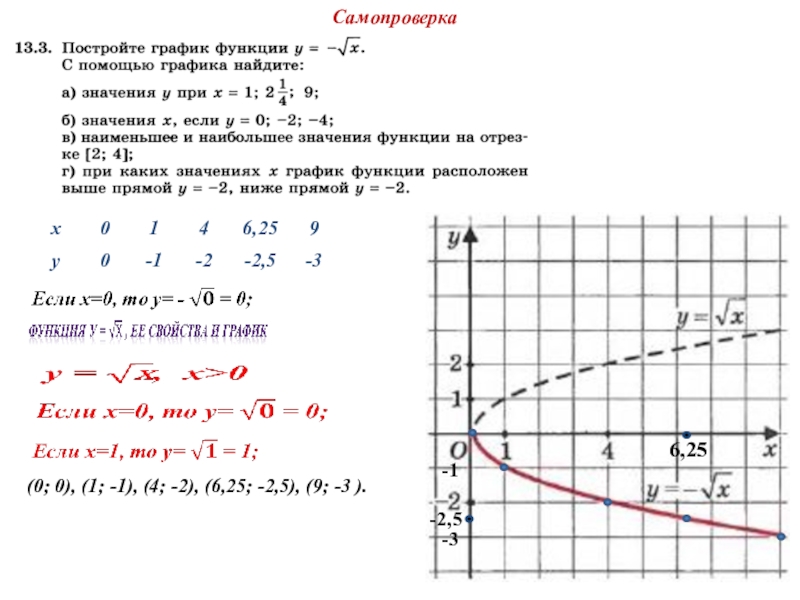
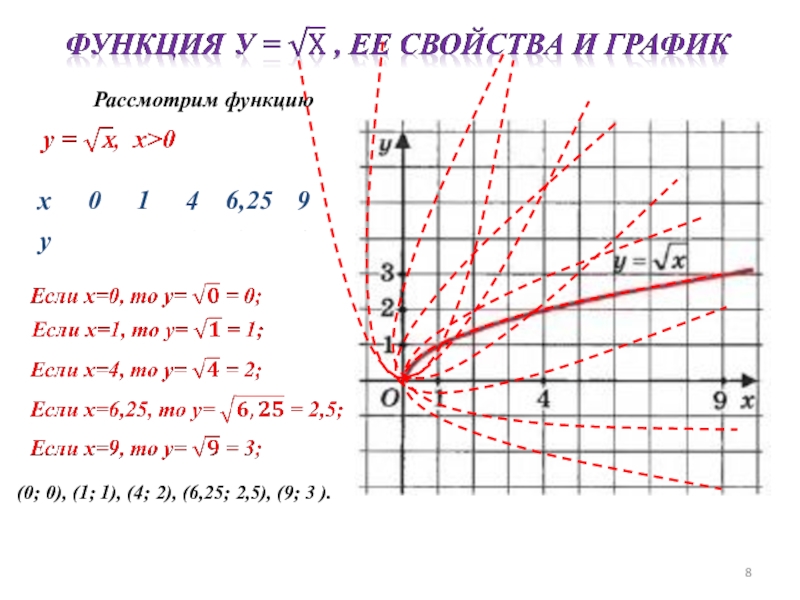
- 8. Рассмотрим функцию(0; 0), (1; 1), (4; 2), (6,25; 2,5), (9; 3 ).
- 9. Рассмотрим свойства функцииСвойство 1. Область
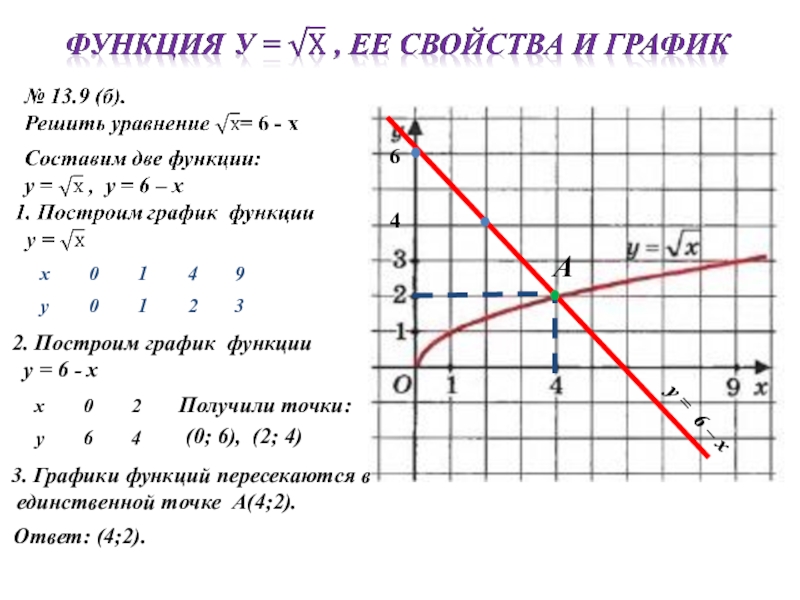
- 10. 2. Построим график функции у = 6
- 11. Задания из задачника:№ 13.2,№ 13.6,---------- № 13.5
- 12. Домашнее задание:§ 13 – учить,№ 13.1,№ 13.3,№ 13.4
- 13. а) б) в) [0; 4]унаиб. = 2,
- 14. (0; 0), (1; -1), (4; -2), (6,25; -2,5), (9; -3 ). -3 -1 -2,56,25Самопроверка
- 15. -3 -1 -2,56,25а) б) в) г) график функции: выше прямой у=-2 при х4.2у = - 2Самопроверка
- 16. Самопроверка
Слайд 3Внимание!
Независимая переменная х имеет степень не выше первой.
Свойства!
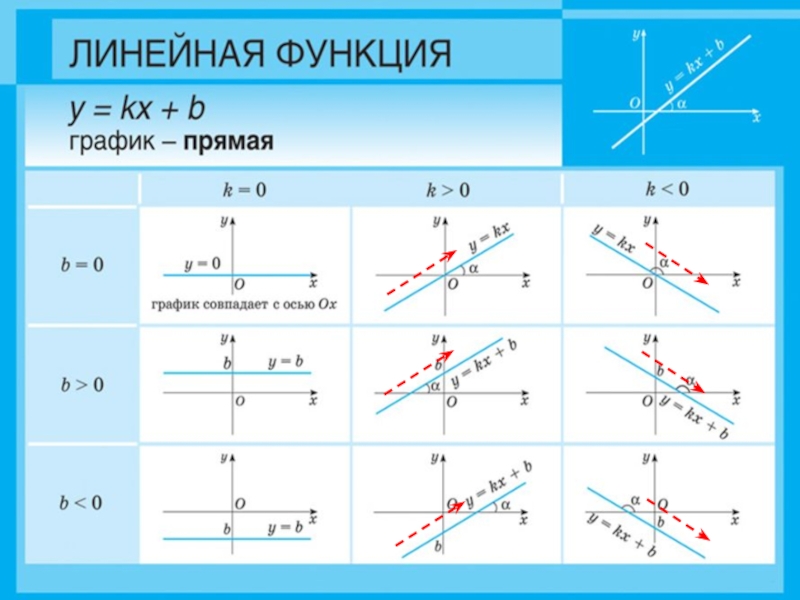
График у = kx
Свойства зависят от коэффициента k (определяет наклон графика, при k = 0 прямая параллельна оси абсцисс или совпадает).
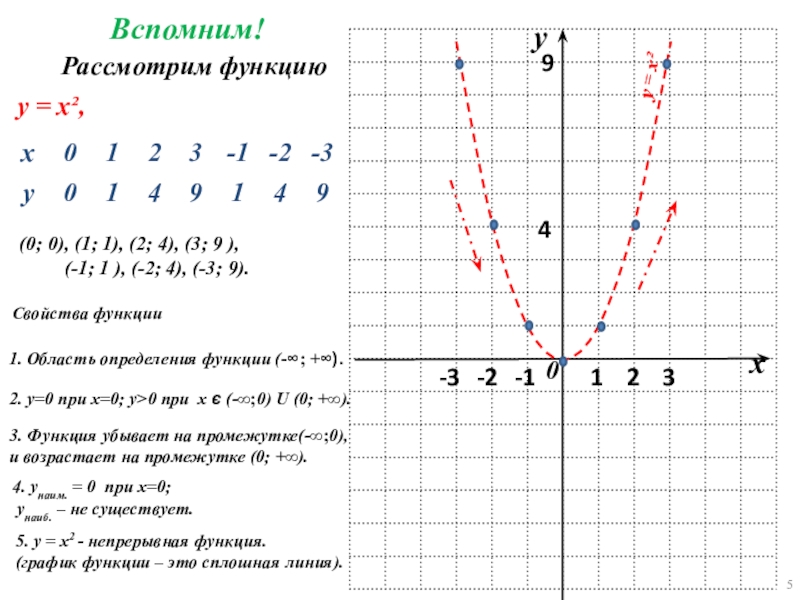
Слайд 5у = х²
(0; 0), (1; 1), (2; 4), (3; 9 ),
Вспомним!
1. Область определения функции (-∞; +∞).
2. у=0 при х=0; у>0 при х є (-∞;0) U (0; +∞).
3. Функция убывает на промежутке(-∞;0),
и возрастает на промежутке (0; +∞).
4. унаим. = 0 при х=0;
унаиб. – не существует.
5. у = х2 - непрерывная функция.
(график функции – это сплошная линия).
Свойства функции
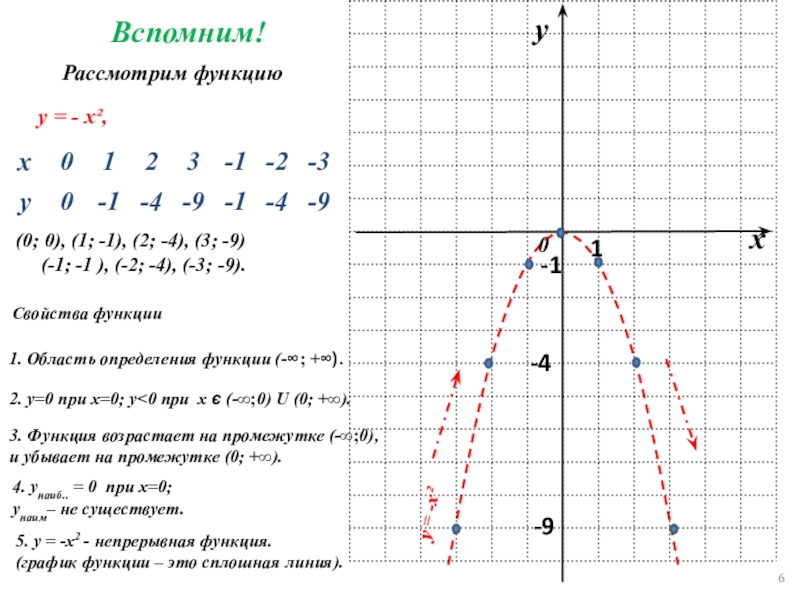
Слайд 6у = -х²
у = - х²,
Рассмотрим функцию
Вспомним!
(0;
(-1; -1 ), (-2; -4), (-3; -9).
-1
-4
-9
1. Область определения функции (-∞; +∞).
2. у=0 при х=0; у<0 при х є (-∞;0) U (0; +∞).
3. Функция возрастает на промежутке (-∞;0),
и убывает на промежутке (0; +∞).
4. унаиб.. = 0 при х=0;
унаим– не существует.
5. у = -х2 - непрерывная функция.
(график функции – это сплошная линия).
Свойства функции
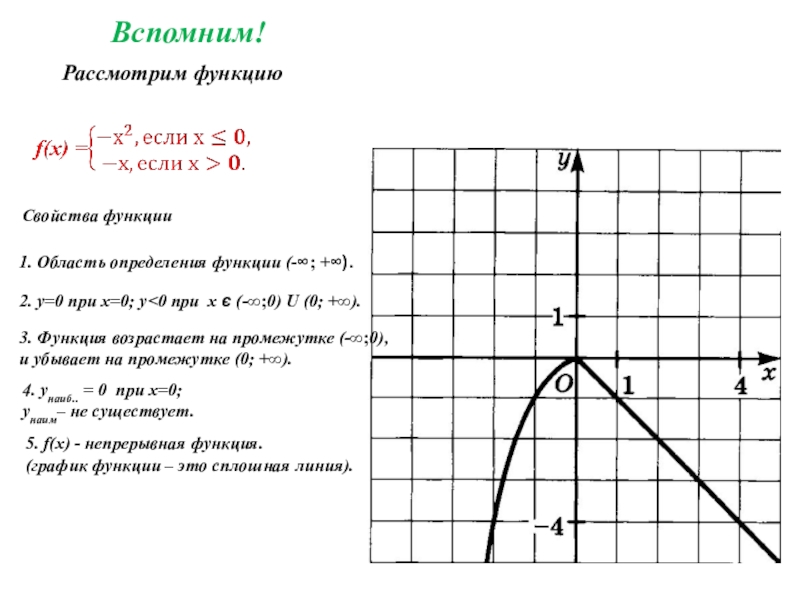
Слайд 7 Рассмотрим функцию
Вспомним!
1. Область определения функции (-∞; +∞).
2. у=0
3. Функция возрастает на промежутке (-∞;0),
и убывает на промежутке (0; +∞).
4. унаиб.. = 0 при х=0;
унаим– не существует.
5. f(x) - непрерывная функция.
(график функции – это сплошная линия).
Свойства функции
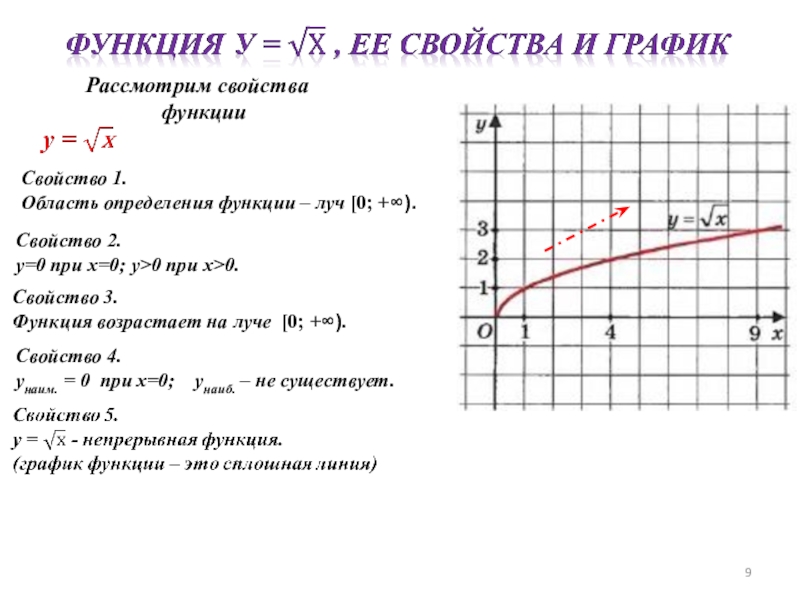
Слайд 9 Рассмотрим свойства функции
Свойство 1.
Область определения функции – луч
Свойство 2.
у=0 при х=0; у>0 при х>0.
Свойство 3.
Функция возрастает на луче [0; +∞).
Свойство 4.
унаим. = 0 при х=0; унаиб. – не существует.
Слайд 102. Построим график функции
у = 6 - х
у
6
4
3. Графики функций пересекаются в
единственной точке А(4;2).
Ответ: (4;2).
А
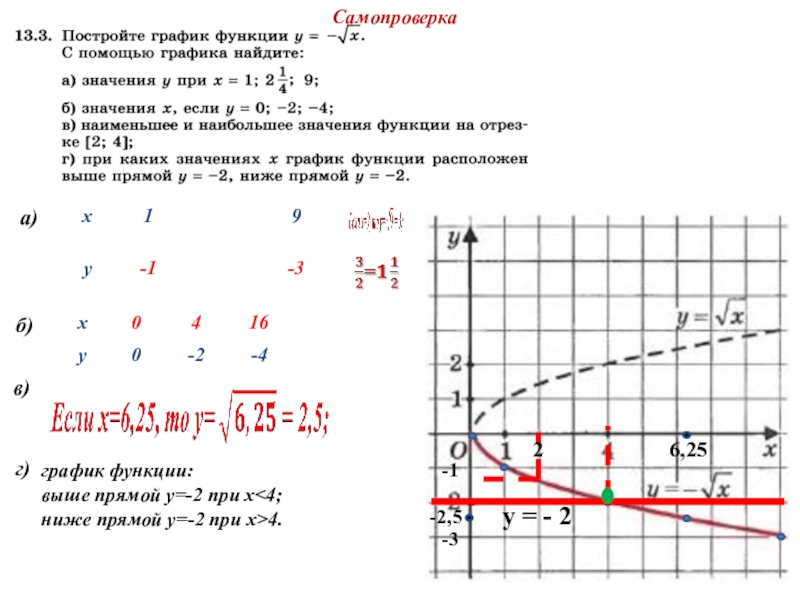
Слайд 13а)
б)
в)
[0; 4]
унаиб. = 2, при х=4;
унаим.
г)
у=1
график функции:
выше прямой у=1 при х>1;
ниже прямой у=1 при х<1.
Самопроверка
![а) б) в) [0; 4]унаиб. = 2, при х=4; унаим. = 0, при х=0.г) у=1график функции:](/img/thumbs/f47d14803dfcde61cd38b025385478a7-800x.jpg "Презентация к уроку алгебры 8 класс по теме Функция у = √х, ее свойства и график а) б) в) [0; 4]унаиб. = 2, при х=4; унаим. =")
Слайд 15-3
-1
-2,5
6,25
а)
б)
в)
г)
график функции:
выше прямой у=-2
ниже прямой у=-2 при х>4.
2
у = - 2
Самопроверка
