- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к технологической карте по теме Теорема Виета (8 класс)
Содержание
- 1. Презентация к технологической карте по теме Теорема Виета (8 класс)
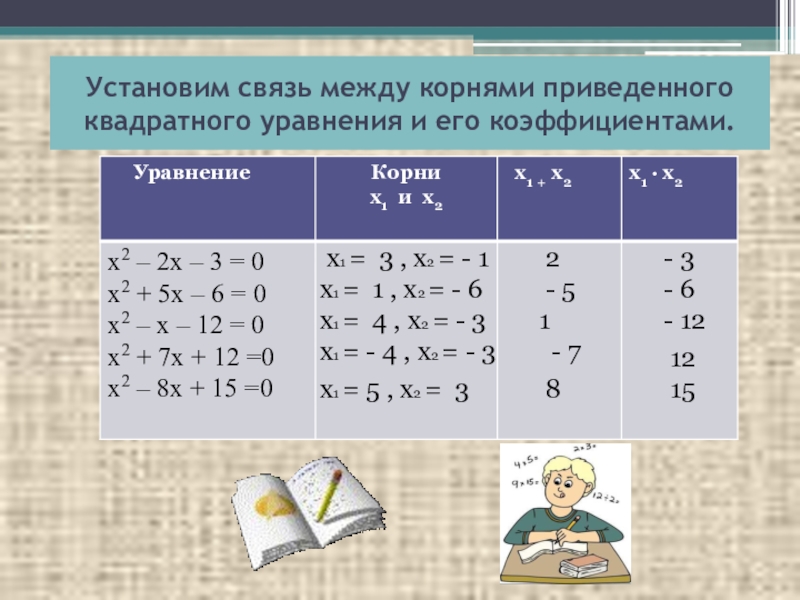
- 2. Установим связь между корнями приведенного квадратного уравнения
- 3. Сумма корней приведенного квадратного уравнения равна второму
- 4. Француз, жил в конце XVI - начале
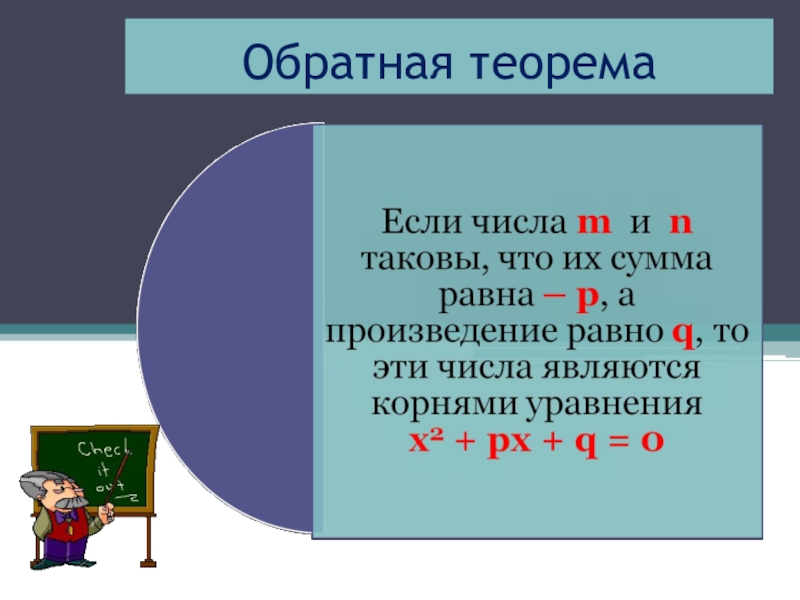
- 5. Обратная теорема
- 6. х2 + px + q = 0x1
- 7. х2 + px + q = 0x1
- 8. х2 + px + q = 0x1
- 9. Составьте квадратное уравнение, имеющее заданные корни х1
- 10. ПРИМЕНЕНИЕ ТЕОРЕМЫПроверяем, правильно ли найдены корни уравнения.Определяем
- 11. Проанализируйте данные и узнайте числа m и
- 12. Для каждого уравнения укажите, если это возможно
- 13. Слайд 13
- 14. Заполните пропускиПо праву достойна в стихах быть
Слайд 2Установим связь между корнями приведенного квадратного уравнения и его коэффициентами.
х1 =
2
- 3
х1 = 1 , х2 = - 6
- 5
- 6
х1 = 4 , х2 = - 3
1
- 12
х1 = - 4 , х2 = - 3
- 7
12
х1 = 5 , х2 = 3
8
15
Слайд 3Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным
х2 + px + q = 0
x1 + x2 = - p
x1 • x2 = q
Знаменитая теорема, устанавливающая связь коэффициентов
приведенного квадратного уравнения с его корнями , была
обнародована в 1591 г. Теперь она носит имя ВИЕТА.
Слайд 4Француз, жил в конце XVI - начале XVII веков, по профессии
Франсуа Виет
(1540 – 1603)
Слайд 6
х2 + px + q = 0
x1 + x2 = -
x1 • x2 = q
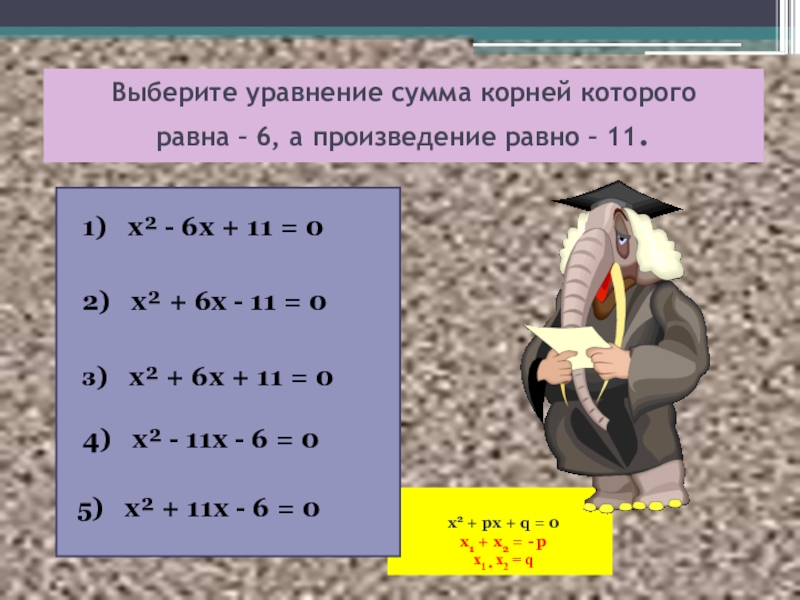
Выберите уравнение сумма корней которого равна – 6, а произведение равно – 11.
1) х² - 6х + 11 = 0
2) х² + 6х - 11 = 0
з) х² + 6х + 11 = 0
4) х² - 11х - 6 = 0
5) х² + 11х - 6 = 0
Слайд 7
х2 + px + q = 0
x1 + x2 = -
x1 • x2 = q
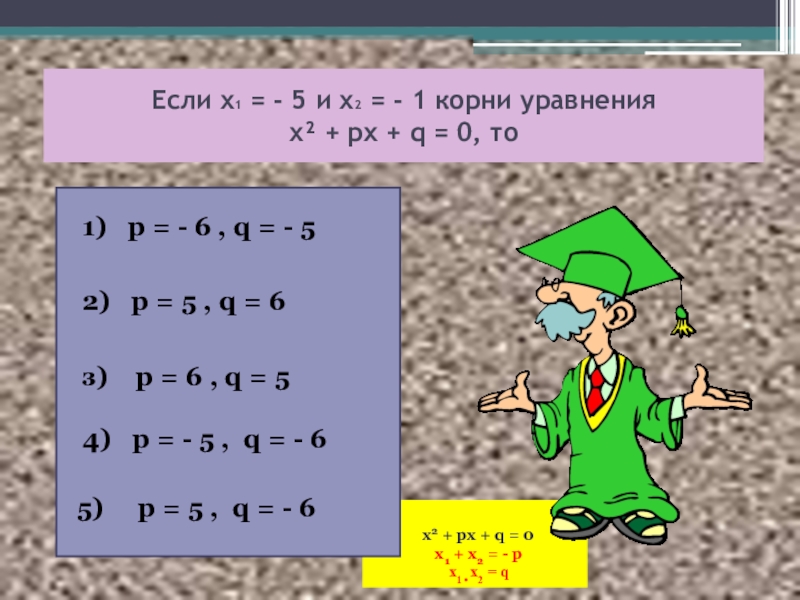
Если х1 = - 5 и х2 = - 1 корни уравнения х² + px + q = 0, то
1) p = - 6 , q = - 5
2) p = 5 , q = 6
з) p = 6 , q = 5
4) p = - 5 , q = - 6
5) p = 5 , q = - 6
Слайд 8
х2 + px + q = 0
x1 + x2 = -
x1 • x2 = q
Найдите сумму и произведение корней уравнения х² - 3х – 5 = 0
(выберите правильный ответ ).
1) х1 + х2= - 3, х1 • х2 = - 5
2) х1 + х2= - 5, х1 • х2 = - 3
З) х1 + х2= 3, х1 • х2 = - 5
4) х1 + х2= 5, х1 • х2 = - 3
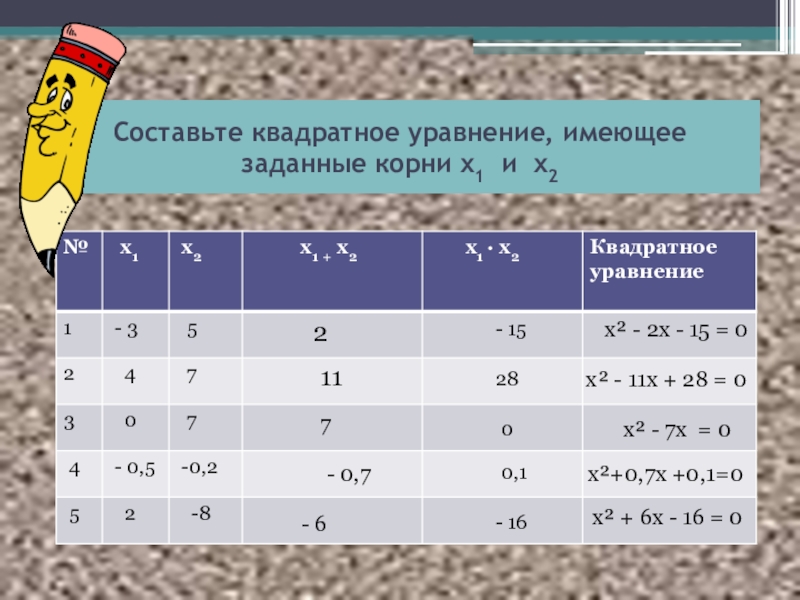
Слайд 9Составьте квадратное уравнение, имеющее заданные корни х1 и х2
2
- 15
11
28
х² - 11х + 28 = 0
7
0
х² - 7х = 0
- 0,7
0,1
х²+0,7х +0,1=0
- 6
- 16
х² + 6х - 16 = 0
Слайд 10ПРИМЕНЕНИЕ ТЕОРЕМЫ
Проверяем, правильно ли найдены корни уравнения.
Определяем знаки корней уравнения не
Устно находим корни приведенного квадратного уравнения.
Составляем квадратное уравнение с заданными корнями.
Слайд 11Проанализируйте данные и узнайте числа m и n
а)
m = ______ n = _______
б) m · n = 15 ; m + n = - 8
m = ______ n = _______
в) m + n = - 2 ; m · n = - 35
m = ______ n = _______
г) m + n = 1 ; m · n = - 12
m = ______ n = _______
7
2
- 3
- 5
- 7
5
4
- 3
Слайд 12Для каждого уравнения укажите, если это возможно сумму и произведение корней.
1)
2) х² + 7х + 12 = 0
з) х² - 8х - 9 = 0
Д > 0, х1 + х2 = 2, х1 ∙ х2 = - 8
Д > 0, х1 + х2 = - 7, х1 ∙ х2 = 12
Д > 0, х1 + х2 = 8, х1 ∙ х2 = - 9
Для каждого уравнения попытайтесь подобрать два числа х1 и х2 так, чтобы выполнялись получившиеся равенства.
2 ∙ (-4) ; - 2 ∙ 4 ; 1 ∙ (-8) ; - 1 ∙ 8
х1 = - 2 , х2 = 4
х1 = - 3 , х2 = - 4
х1 = - 1 , х2 = 9
Слайд 13
x² + b/a x + c/a = 0
По теореме Виета
x1 + x2 = - b/a
x1 ∙ x2 = c/a
Используя теорему Виета, можно выразить сумму и произведение корней произвольного квадратного уравнения через его коэффициенты.
Слайд 14Заполните пропуски
По праву достойна в стихах быть воспета
О свойстве корней теорема___________
Что
Умножишь ты корни, и дробь уж готова:
В числителе «____», в знаменателе «а».
И сумма корней тоже дроби равна.
Хоть с минусом дробь эта, что за беда
В числителе «____», а в знаменателе – «____».
Виета
c
b
a