- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к проекту по математике 10 способов решения КВУР
Содержание
- 1. Презентация к проекту по математике 10 способов решения КВУР
- 2. D = b² - 4acПроблема: насколько разнообразны
- 3. ИсторияИз истории возникновения квадратных уравненийАлгебра возникла в
- 4. В «Арифметике» Диофанта нет систематического изложения алгебры,
- 5. Если решить эту задачу, выбирая в качестве
- 6. Квадратные уравнения в ИндииЗадачи на
- 7. Решение Бхаскары свидетельствует о том, что автор
- 8. Квадратные уравнения у Аль-ХорезмиВ алгебраическом трактате Аль-Хорезми
- 9. Приведем пример.Задача 4. «Квадрат и число 21
- 10. 10 способов решение квадратных уравнений 1) Разложение
- 11. Разложение левой части уравнения на множителиРешим уравнение
- 12. Метод выделения полного квадрата Решим уравнение х2
- 13. Решений квадратных уравнений с помощью дискриминанта ЗАПОМНИ!D
- 14. Решение с помощью теоремы Виетаx2 + px
- 15. Запомни!!!x2 + px + q = 0x1
- 16. Метод переброскиРешить уравнение 6x2 – 7x –
- 17. Геометрический способ решение квадратных уравненийВ древности, когда
- 18. Решение квадратных уравнений с помощью номограммыz2 +
- 19. Свойства коэффициента квадратного уравненияПусть дано квадратное уравнение
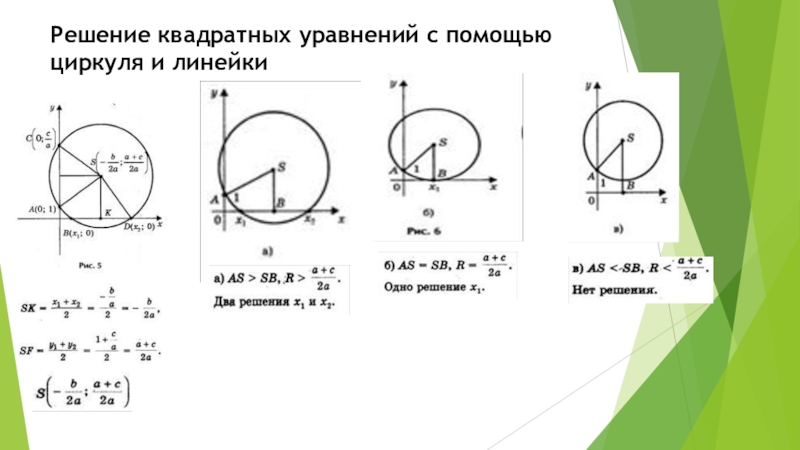
- 20. Решение квадратных уравнений с помощью циркуля и
- 21. 10.Графическое решение квадратных уравнений Первый способ.Построим график
- 22. Третий способ. Преобразуем уравнение к виду x2−3=2x. Построим
- 23. Четвёртый способ.Преобразуем уравнение к виду x2−2x+1−4=0 и
- 24. Вывод При работе над темой мы ставили
- 25. формулу нахождения дискриминанта;формулу нахождения корней квадратного уравнения;алгоритмы
Слайд 1Муниципальное общеобразовательное учреждение
«Средняя школа №30»
Проект
по математике
на тему:
«10 способов решения
Выполнили ученики 8В класса
Данил Гордеев
Андрей Алферов
Руководитель:
Новикова С.А.
2018
Слайд 2D = b² - 4ac
Проблема: насколько разнообразны способы решения квадратных уравнений
Гипотеза:
Планируемый продукт: буклет
Цель работы: изучение теории по теме и применение на практике различных способов решения квадратных уравнений
Из данной цели нами были поставлены
задачи:
-узнать историю квадратных уравнений
-узнать новые способы решения квадратных уравнений
-выявить наиболее удобные способы решения квадратных уравнений
-научиться решать квадратные уравнения разными способами
Слайд 3История
Из истории возникновения квадратных уравнений
Алгебра возникла в связи с решением разнообразных
Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне.
Квадратные уравнения в Древнем Вавилоне
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
Слайд 4В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.
Вот, к примеру, одна из его задач.
Задача 2. «Найти два числа, зная, что их сумма равна 20, а произведение — 96».
Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10 + х. Другое же меньше, т. е. 10 - х. Разность между ними 2х. Отсюда уравнение:
(10+x)(10—x) =96,
или же
100 —x2 = 96.
x2 - 4 = 0
Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = - 2 для Диофанта не существует, так как греческая математика знала только положительные числа.
Слайд 5Если решить эту задачу, выбирая в качестве неизвестного одно из искомых
y (20-y)=96
y2 - 20y+96=0
Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения.
Слайд 6
Квадратные уравнения в Индии
Задачи на квадратные уравнения встречаются уже
ax2 + bх = с, а>
В уравнении (1) коэффициенты, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары.
Задача 3.
«Обезьянок резвых стая
Всласть поевши, развлекалась
Их в квадрате часть восьмая
На поляне забавлялась
А двенадцать по лианам
Стали прыгать, повисая
Сколько ж было обезьянок,
Ты скажи мне, в этой стае?»
Слайд 7Решение Бхаскары свидетельствует о том, что автор знал о двузначности корней
Соответствующее задаче 3 уравнение:
Бхаскара пишет под видом:
x2 - 64x = - 768
и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 322, получая затем:
x2 - б4х + 322 = -768 + 1024,
(х - 32)2 = 256,
х - 32= ±16,
x1 = 16, x2 = 48.
Слайд 8Квадратные уравнения у Аль-Хорезми
В алгебраическом трактате Аль-Хорезми дается классификация линейных и
1) «Квадраты равны корням», т. е. ах2 = bх.
2) «Квадраты равны числу», т. е. ах2 = с.
3) «Корни равны числу», т. е. ах = с.
4) «Квадраты и числа равны корням», т. е. ах2 + с = bх.
5) «Квадраты и корни равны числу», т. е. ах2 + bх =с.
6) «Корни и числа равны квадратам», т. е. bх + с == ах2.
Для Аль-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида Аль-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.
Слайд 9Приведем пример.
Задача 4. «Квадрат и число 21 равны 10 корням. Найти
Решение: раздели пополам число корней, получишь 5, умножь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от 5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.
Трактат Аль-Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.[3,75]
Слайд 1010 способов решение квадратных уравнений
1) Разложение левой части уравнения на
2) Метод выделения полного квадрата;
3) Решений квадратных уравнений с помощью дискриминанта;
4) Решение с помощью теоремы Виета;
5) Решение с помощью «переброски»;
6) Решение квадратного уравнения геометрическим способом
7) Решение квадратного уравнения с помощью номограммы
8) Свойство коэффициентов квадратного уравнения
9) Решение квадратных уравнений с помощью циркуля и линейки
10) Графический способ решения квадратных уравнений
Слайд 11Разложение левой части уравнения на множители
Решим уравнение х2 + 10х -
х2 + 10х - 24 = х2 + 12х - 2х - 24 = х (х + 12) - 2 (х + 12) = (х + 12) (х - 2).
Следовательно, уравнение можно переписать так:
(х + 12) (х - 2) = 0
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = - 12. Это означает, что число 2 и - 12 являются корнями уравнения х2 + 10х - 24 = 0.
Слайд 12Метод выделения полного квадрата
Решим уравнение х2 + 6х - 7 =
Для этого запишем выражение х2 + 6х в следующем виде:
х2 + 6х = х2 + 2* х * 3.
В полученном выражении первое слагаемое - квадрат числа х, а второе - удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 32, так как
х2 + 2* х * 3 + 32 = (х + 3)2.
Преобразуем теперь левую часть уравнения
х2 + 6х - 7 = 0,
прибавляя к ней и вычитая 32. Имеем:
х2 + 6х - 7 = х2 + 2* х * 3 + 32 - 32 - 7 = (х + 3)2 - 9 - 7 = (х + 3)2 - 16.
Таким образом, данное уравнение можно записать так:
(х + 3)2 - 16 =0, (х + 3)2 = 16.
Следовательно, х + 3 - 4 = 0, х1 = 1, или х + 3 = -4, х2 = -7.
Слайд 13Решений квадратных уравнений с помощью дискриминанта
ЗАПОМНИ!
D = b2 – 4ас
ах2 + b
Слайд 14Решение с помощью теоремы Виета
x2 + px + q = 0-Приведенное
p = b
q = c
x2 + px + q = 0
=
ax2 + bx + c = 0
Слайд 15Запомни!!!
x2 + px + q = 0
x1 + x2 = −p
x1 · x2 = q
где «x1» и «x2» — корни этого уравнения.
Пример:
x2 + 4x − 5 = 0
a = 1
p = 4
q = −5
x1 + x2 = −4
x1 · x2 = −5
Ответ: x1 = −5; x2 = 1
Проверим подстановкой
−5 + 1 = −4
−5 · 1 = −5
Слайд 16Метод переброски
Решить уравнение 6x2 – 7x – 3 = 0.
Решение.
Выполним «переброску»
Виета:
y2 – 7y – 3 · 6 = 0; x1 = y1 / 6 = 9 / 6 = 1.5
y2 – 7y – 18 = 0. x2 = y2 / 6 = -2 / 6 = -1/3
y1 + y2 = – p Ответ: -1/3; 1,5.
y1 · y2 = q
y1 = 9
y2 = -2
Слайд 17Геометрический способ решение квадратных уравнений
В древности, когда геометрия была более развита,
Примеры.
Решим уравнение х2 + 10х = 39.
В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39» (рис.15).
Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата, сторона каждого их них 2,5, а площадь 6,25.
Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х2, четырех прямоугольников (4• 2,5х = 10х) и четырех пристроенных квадратов (6,25• 4 = 25), т.е. S = х2 + 10х + 25. Заменяя
х2 + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим
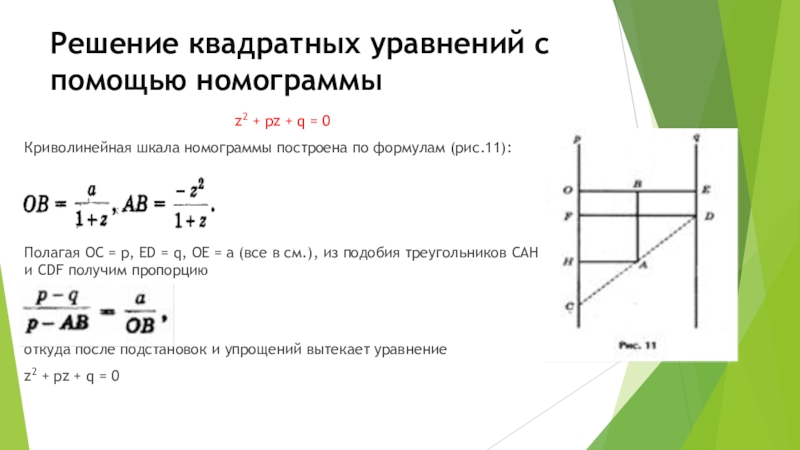
Слайд 18Решение квадратных уравнений с помощью номограммы
z2 + pz + q =
Криволинейная шкала номограммы построена по формулам (рис.11):
Полагая ОС = р, ED = q, ОЕ = а (все в см.), из подобия треугольников САН и CDF получим пропорцию
откуда после подстановок и упрощений вытекает уравнение
z2 + pz + q = 0
Слайд 19Свойства коэффициента квадратного уравнения
Пусть дано квадратное уравнение ах2 + bх +
1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1,
х2 = с/а.
Доказательство. Разделим обе части уравнения на а ? 0, получим приведенное квадратное уравнение
x2 + b/a * x + c/a = 0.
Согласно теореме Виета
x1 + x2 = - b/a,
x1x2 = 1* c/a.
По условию а - b + с = 0, откуда b = а + с. Таким образом,
x1 + x2 = - а + b/a= -1 - c/a,
x1x2 = - 1* (- c/a),
т.е. х1 = -1 и х2 = c/a, что м требовалось доказать.
* Примеры.
1) Решим уравнение 345х2 - 137х - 208 = 0.
Решение. Так как а + b + с = 0 (345 - 137 - 208 = 0), то
х1 = 1, х2 = c/a = -208/345.
Ответ: 1; -208/345.
2) Решим уравнение 132х2 - 247х + 115 = 0.
Решение. Так как а + b + с = 0 (132 - 247 + 115 = 0), то
х1 = 1, х2 = c/a = 115/132.
Ответ: 1; 115/132.
Слайд 2110.Графическое решение квадратных уравнений
Первый способ.
Построим график функции x2−2x−3=0.
1. Имеем: a=1,b=−2,x0=−b2a=1,y0=f(1)=12−2−3=−4. Значит,
2. Возьмём на оси x две точки, симметричные относительно оси параболы, например точки x=−1 и x=3. Имеем f(−1)=f(3)=0. Построим на координатной плоскости точки (−1;0)и(3;0).
3. Через точки (−1;0),(1;−4),(3;0) проводим параболу.
Корнями уравнения x2−2x−3=0 являются абсциссы точек пересечения параболы с осью х; значит, корни уравнения таковы: x1=−1;x2=3.
Слайд 22Третий способ.
Преобразуем уравнение к виду x2−3=2x. Построим в одной системе координат
Они пересекаются в двух точках C(−1;−2) и D(3;6). Корнями уравнения являются абсциссы точек C и D, поэтому x1=−1;x2=3.
Второй способ.
Преобразуем уравнение к виду x2=2x+3. Построим в одной системе координат графики функций: y=x2;y=2x+3.
Они пересекаются в двух точках C(−1;1) и D(3;9). Корнями уравнения служат абсциссы точек C и D, значит, x1=−1;x2=3.
Слайд 23Четвёртый способ.
Преобразуем уравнение к виду x2−2x+1−4=0 и далее x2−2x+1=4→(x−1)2=4.
Построим в одной
Они пересекаются в двух точках C(−1;4) и D(3;4). Корнями уравнения служат абсциссы точек C и D, поэтому x1=−1;x2=3.
Пятый способ.
Разделив почленно обе части уравнения на x, получим x−2−3x=0x−2=3x
Построим в одной системе координат гиперболу y=3x и прямую y=x−2.
Они пересекаются в двух точках A(−1;−3) и B(3;1). Корнями уравнения являются абсциссы точек A и B, следовательно, x1=−1;x2=3.
Итак, квадратное уравнение x2−2x−3=0 мы решили графически пятью способами.
Слайд 24Вывод
При работе над темой мы ставили задачу выяснить какие методы
Итак, стандартные методы (используются чаще при решении квадратных уравнений):
Решение квадратных уравнений по формулам
Теорема Виета
Графическое решение уравнений
Разложение левой части на множители
Выделение полного квадрата
Нестандартные методы:
Решение способом переброски коэффициентов
Свойства коэффициентов квадратного уравнения
Решение квадратных уравнений, с помощью циркуля и линейки.
Решение с помощью номограммы
Геометрический способ
При решении квадратных уравнений мы сделали следующие выводы: Для того, чтобы хорошо решать любое квадратные уравнения необходимо знать:
Слайд 25формулу нахождения дискриминанта;
формулу нахождения корней квадратного уравнения;
алгоритмы решения уравнений данного вида.
уметь:
решать полные квадратные уравнения;
решать приведенные квадратные уравнения;
находить ошибки в решенных уравнениях и исправлять их;
делать проверку.
Думаем, что наша работа будет интересна учащимся 8 классов, а также тем, которые хотят
научиться решать рационально квадратные уравнения и хорошо подготовиться к
выпускным экзаменам. Наша работа, также будет интересна и учителям математики, так как в своей работе мы не только рассмотрели методы решения квадратных уравнений, но и историю их развития.