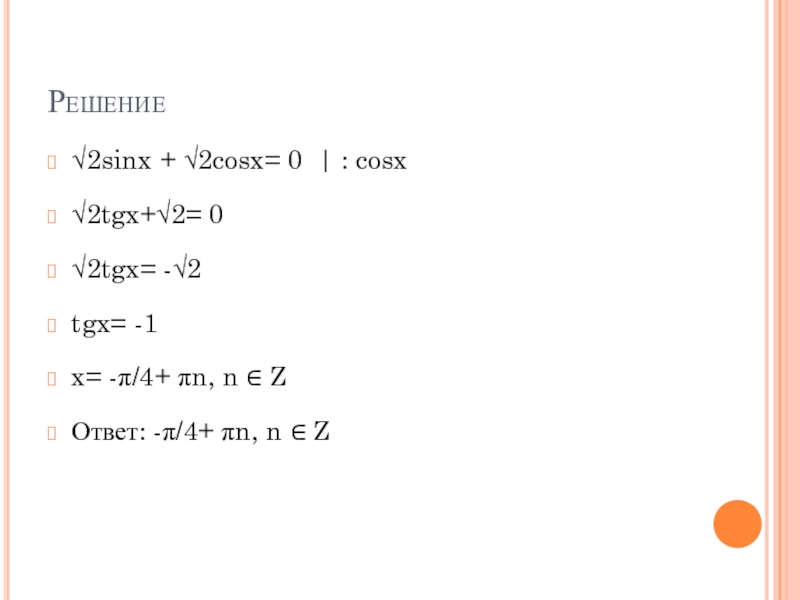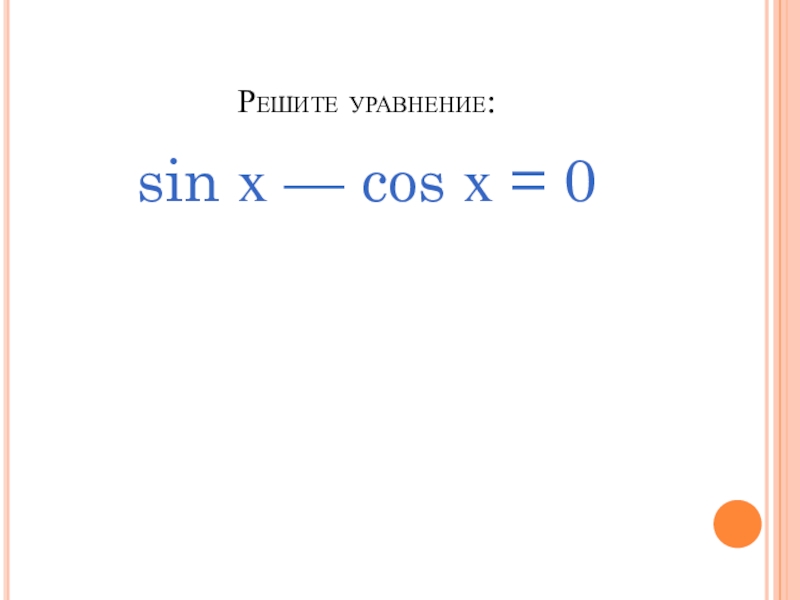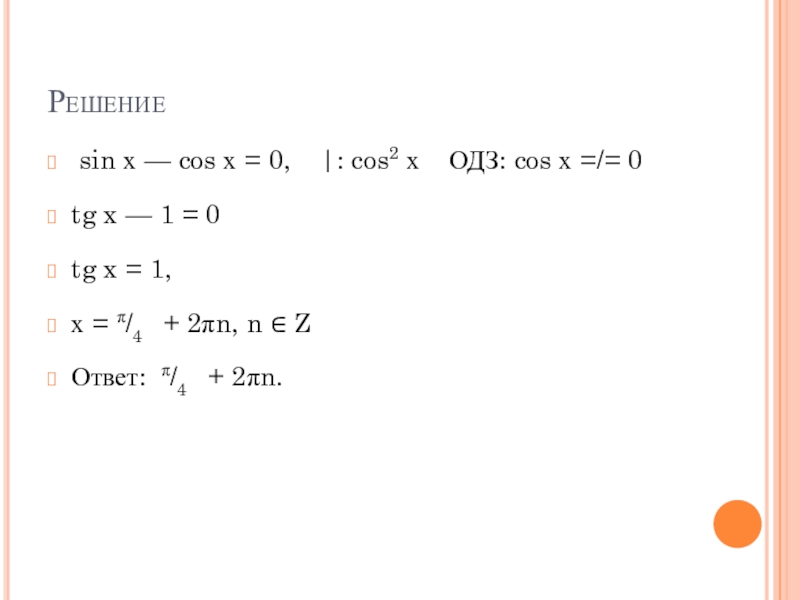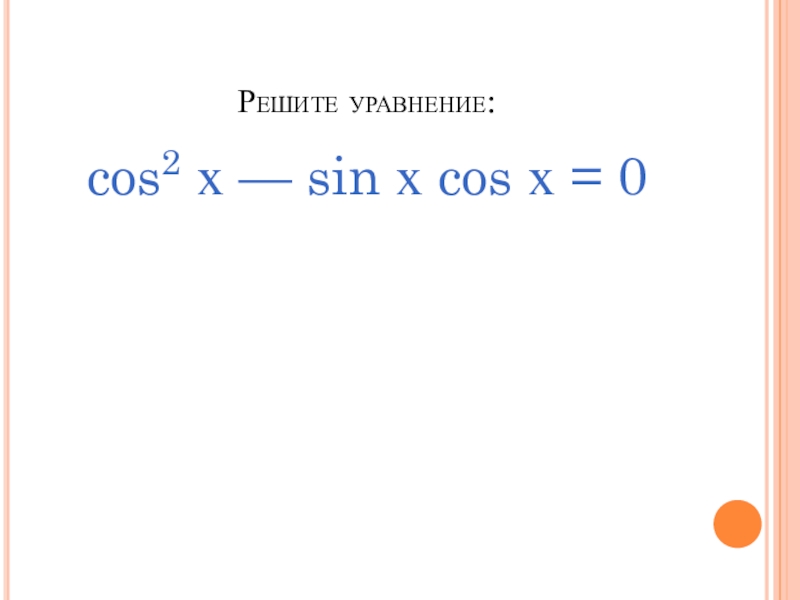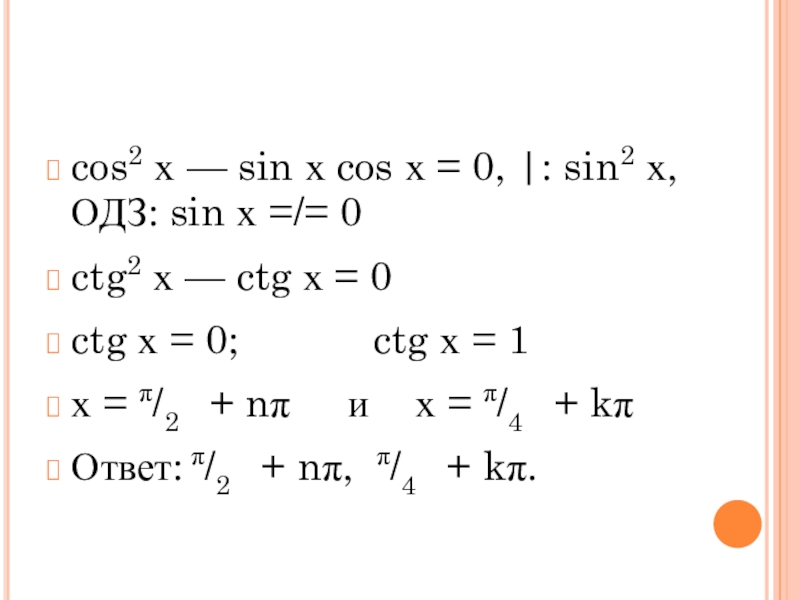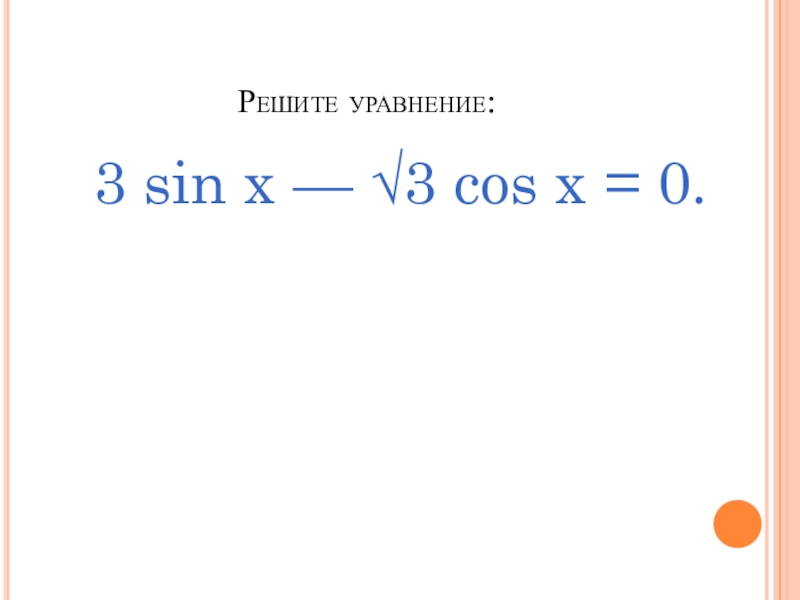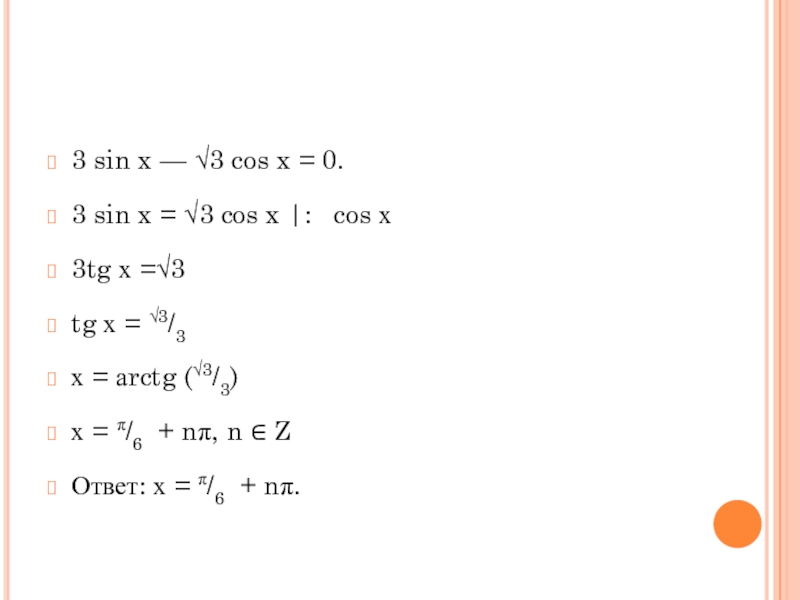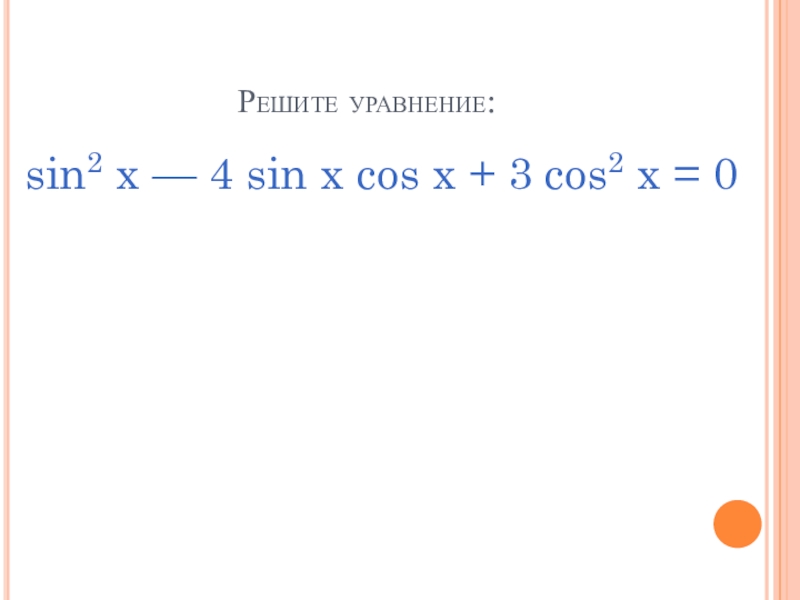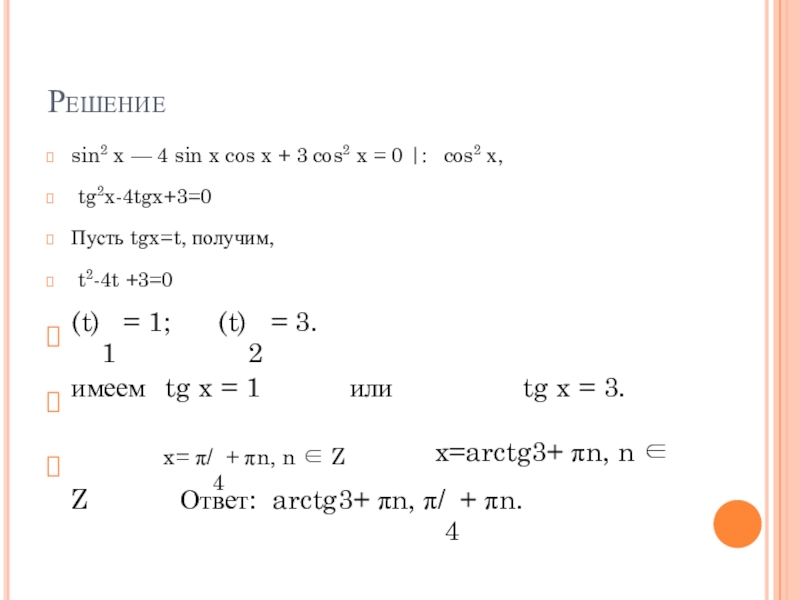класса А
Соловьева Регина
и
Габдрахманова Динара
Руководитель: учитель математики Морозова Татьяна Николаевна
г.Нижнекамск
2017-2018 учебный год
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к проектной работе Однородные уравнения
Содержание
- 1. Презентация к проектной работе Однородные уравнения
- 2. Однородные тригонометрические уравнения Определение 1. Уравнение вида
- 3. Пример: Решим уравнение 2 sin
- 4. Алгоритм решения однородного уравнения второй степениУсловие: в
- 5. Решите уравнение:2cos2x – sinxcosx + 5sin2x=3
- 6. Решение2cos2x – sinxcosx + 5sin2x=32cos 2 x
- 7. Решите уравнение:√2sinx + √2cosx= 0
- 8. Решение√2sinx + √2cosx= 0 | : cosx√2tgx+√2=
- 9. Решите уравнение:sin х — cos х = 0
- 10. Решение sin х — cos х = 0, |: cos2 х
- 11. Решите уравнение:sin2 х — 5 sin х cos х + 6 cos2 х = 0
- 12. Решениеsin2 х — 5 sin х cos х + 6 cos2 х = 0, |:
- 13. Решите уравнение:cos2 х — sin х cos х = 0
- 14. cos2 х — sin х cos х = 0, |: sin2 х,
- 15. Решите уравнение:3 sin x — √3 cos x = 0.
- 16. 3 sin x — √3 cos x = 0.3 sin x = √3 cos x |: cos х3tg х =√3 tg х = √3/3 х = аrctg (√3/3)х = π/6 + nπ, n ∈ Z Ответ: х = π/6 + nπ.
- 17. Решите уравнение:sin2 x — 4 sin x cos x + 3 cos2 x = 0
- 18. Решениеsin2 x — 4 sin x cos x + 3 cos2 x = 0 |:
Однородные тригонометрические уравнения Определение 1. Уравнение вида а sin x + b cos x = 0 называют однородным тригонометрическим уравнением первой степени. Определение 2. Уравнение вида a sin^2x + b cos^2x =0 называют однородным тригонометрическим уравнением
Слайд 2Однородные тригонометрические уравнения
Определение 1.
Уравнение вида а sin x +
b cos x = 0 называют однородным тригонометрическим уравнением первой степени.
Определение 2.
Уравнение вида a sin^2x + b cos^2x =0 называют однородным тригонометрическим уравнением второй степени.
Алгоритм решения однородного уравнения первой степени a sin x + b cos x = 0:
1) разделить обе части уравнения на cos x
2) решить получившееся выражение
Определение 2.
Уравнение вида a sin^2x + b cos^2x =0 называют однородным тригонометрическим уравнением второй степени.
Алгоритм решения однородного уравнения первой степени a sin x + b cos x = 0:
1) разделить обе части уравнения на cos x
2) решить получившееся выражение
Слайд 3
Пример:
Решим уравнение
2 sin x – 3 cos x = 0.
Решение:
Разделим
обе части уравнения на cos x:
Получаем:
2 tg x – 3 = 0
2 tg x = 3
tg x =3/2
x = arctg 3/2+ πn, n ∈ Z
Ответ: arctg 3/2+ πn, n ∈ Z
Получаем:
2 tg x – 3 = 0
2 tg x = 3
tg x =3/2
x = arctg 3/2+ πn, n ∈ Z
Ответ: arctg 3/2+ πn, n ∈ Z
Слайд 4Алгоритм решения однородного уравнения второй степени
Условие: в уравнении должно быть выражение
вида a sin^2 x. Если его нет, то уравнение решается методом разложения на множители.
1) Разделить обе части уравнения на cos2 х
2) Ввести новую переменную t, заменяющую tg x (то есть t= tg x)
3) Решить получившееся уравнение
6sin2 х-3sinxcosx-cos2x=1
Используем равенство: sin2x+ cos2x=1
6sin 2 x- 3sinxcosx-cos2x- sin2x- cos2x=0
5sin 2 x- 3sinxcosx- 2cos2x=0 |: cos2x,
5tg 2 x- 3tgx-2=0
Пусть tgx= t, получим
5t 2 -3t-2=0
D=49=7 2
t1 = -0,4 ; t2= 1
Имеем tg x= -0, 4 или tgx= 1
х= - arctg0,4+ πn, n ∈ Z ; x= π/4 + πn, n ∈ Z
Ответ: = - arctg0,4+ πn, n ∈ Z ; x= π/4 + πn, n ∈ Z
1) Разделить обе части уравнения на cos2 х
2) Ввести новую переменную t, заменяющую tg x (то есть t= tg x)
3) Решить получившееся уравнение
6sin2 х-3sinxcosx-cos2x=1
Используем равенство: sin2x+ cos2x=1
6sin 2 x- 3sinxcosx-cos2x- sin2x- cos2x=0
5sin 2 x- 3sinxcosx- 2cos2x=0 |: cos2x,
5tg 2 x- 3tgx-2=0
Пусть tgx= t, получим
5t 2 -3t-2=0
D=49=7 2
t1 = -0,4 ; t2= 1
Имеем tg x= -0, 4 или tgx= 1
х= - arctg0,4+ πn, n ∈ Z ; x= π/4 + πn, n ∈ Z
Ответ: = - arctg0,4+ πn, n ∈ Z ; x= π/4 + πn, n ∈ Z
Слайд 6Решение
2cos2x – sinxcosx + 5sin2x=3
2cos 2 x – sinxcosx + 5sin
2 x=3(sin 2 x+cos 2)
2sin 2 x- sinxcosx –cos 2 =0 | cos 2 x
2tg 2 x- tgx-1=0
Пусть tgx= t, получим
2t 2 -t-1=0
D=9= 3 2
t 1= - 1/2 ; t 2=1
Имеем tg x= - 1/2 или tg x=1
х= -arctg 1/2 + πn, n ∈ Z х= π/4 + πn, n ∈ Z
Ответ: -arctg 1/2 + πn, n ∈ Z; π/4 + πn, n ∈ Z
2sin 2 x- sinxcosx –cos 2 =0 | cos 2 x
2tg 2 x- tgx-1=0
Пусть tgx= t, получим
2t 2 -t-1=0
D=9= 3 2
t 1= - 1/2 ; t 2=1
Имеем tg x= - 1/2 или tg x=1
х= -arctg 1/2 + πn, n ∈ Z х= π/4 + πn, n ∈ Z
Ответ: -arctg 1/2 + πn, n ∈ Z; π/4 + πn, n ∈ Z
Слайд 8Решение
√2sinx + √2cosx= 0 | : cosx
√2tgx+√2= 0
√2tgx= -√2
tgx= -1
x= -π/4+
πn, n ∈ Z
Ответ: -π/4+ πn, n ∈ Z
Ответ: -π/4+ πn, n ∈ Z
Слайд 10Решение
sin х — cos х = 0, |: cos2 х ОДЗ: cos х =/= 0
tg x — 1
= 0
tg x = 1,
х = π/4 + 2πn, n ∈ Z
Ответ: π/4 + 2πn.
tg x = 1,
х = π/4 + 2πn, n ∈ Z
Ответ: π/4 + 2πn.
Слайд 12Решение
sin2 х — 5 sin х cos х + 6 cos2 х = 0, |: cos2 х, ОДЗ:
cos х =/= 0
tg2 х — 5 tg х + 6 = 0;
Пусть tg x=t,получим
t2-5t+6=0
D=1
t1 = 2; t2= 3
имеем tg x = 2; или tg x = 3.
x = arctg 2 + πn, n ∈ Z х = arctg 3 + πn, n ∈ Z
Ответ: arctg 2 + πn, arctg 3 + πn.
tg2 х — 5 tg х + 6 = 0;
Пусть tg x=t,получим
t2-5t+6=0
D=1
t1 = 2; t2= 3
имеем tg x = 2; или tg x = 3.
x = arctg 2 + πn, n ∈ Z х = arctg 3 + πn, n ∈ Z
Ответ: arctg 2 + πn, arctg 3 + πn.
Слайд 14cos2 х — sin х cos х = 0, |: sin2 х, ОДЗ: sin х =/= 0
ctg2 х — ctg х =
0
ctg х = 0; ctg х = 1
х = π/2 + nπ и х = π/4 + kπ
Ответ: π/2 + nπ, π/4 + kπ.
ctg х = 0; ctg х = 1
х = π/2 + nπ и х = π/4 + kπ
Ответ: π/2 + nπ, π/4 + kπ.
Слайд 163 sin x — √3 cos x = 0.
3 sin x = √3 cos x |: cos х
3tg х =√3
tg х = √3/3
х = аrctg (√3/3)
х = π/6 + nπ,
n ∈ Z
Ответ: х = π/6 + nπ.
Ответ: х = π/6 + nπ.
Слайд 18Решение
sin2 x — 4 sin x cos x + 3 cos2 x = 0 |: cos2 х,
tg2x-4tgx+3=0
Пусть
tgx=t, получим,
t2-4t +3=0
(t)1 = 1; (t)2 = 3.
имеем tg x = 1 или tg x = 3.
x= π/4+ πn, n ∈ Z x=arctg3+ πn, n ∈ Z Ответ: arctg3+ πn, π/4+ πn.
t2-4t +3=0
(t)1 = 1; (t)2 = 3.
имеем tg x = 1 или tg x = 3.
x= π/4+ πn, n ∈ Z x=arctg3+ πn, n ∈ Z Ответ: arctg3+ πn, π/4+ πn.