- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к открытому уроку
Содержание
- 1. Презентация к открытому уроку
- 2. Вопросы Что такое комбинаторика?От какого слова произошло слово «комбинаторика»?Какие приемы решения комбинаторных задач вы знаете?
- 3. - раздел математики, в котором изучаются вопросы
- 4. Термин «комбинаторика» был введён в математический обиход
- 5. Некоторые приемы решения комбинаторных задач решение
- 6. Люди, которые умело владеют техникой решения комбинаторных
- 7. №715 (д\з)У Ирины 5 подруг: Вера, Зоя,
- 8. Составим сначала все пары, в которые входит
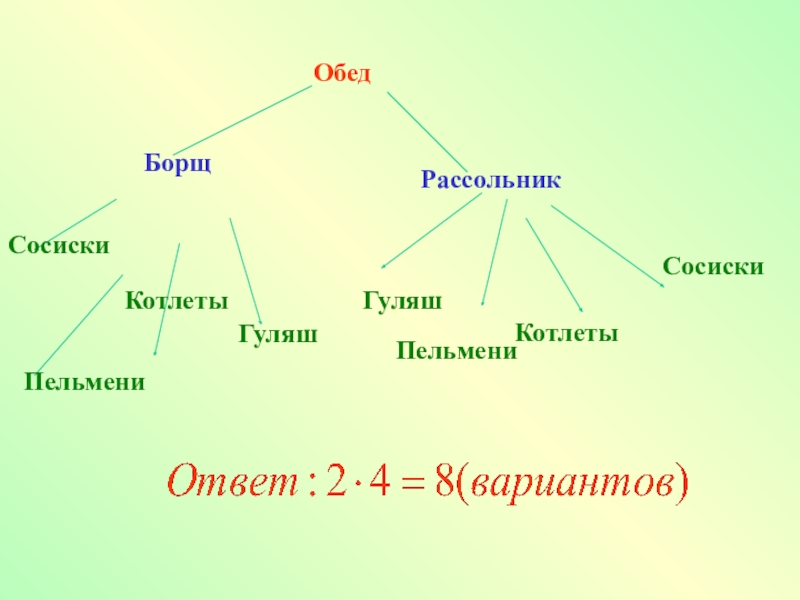
- 9. Задача №714.БорщРассольник Гуляш Котлета Сосиски
- 10. ОбедКотлетыРассольник Борщ Гуляш Гуляш Сосиски ПельмениСосискиКотлетыПельмени
- 11. Рассмотрим задачу. На цветочной клумбе сидели шмель,
- 12. РешениеВсего 3+2+1=6Ответ:6 вариантовшшшжжбббжммм
- 13. Слайд 13
- 14. дерево возможных вариантов Решим задачу о
- 15. Заметим, что ответ на вопрос,
- 16. «Если объект А можно выбрать m способами,
- 17. У Куклы Светы 3 юбки и 5
- 18. Решите задачу, используя дерево возможных
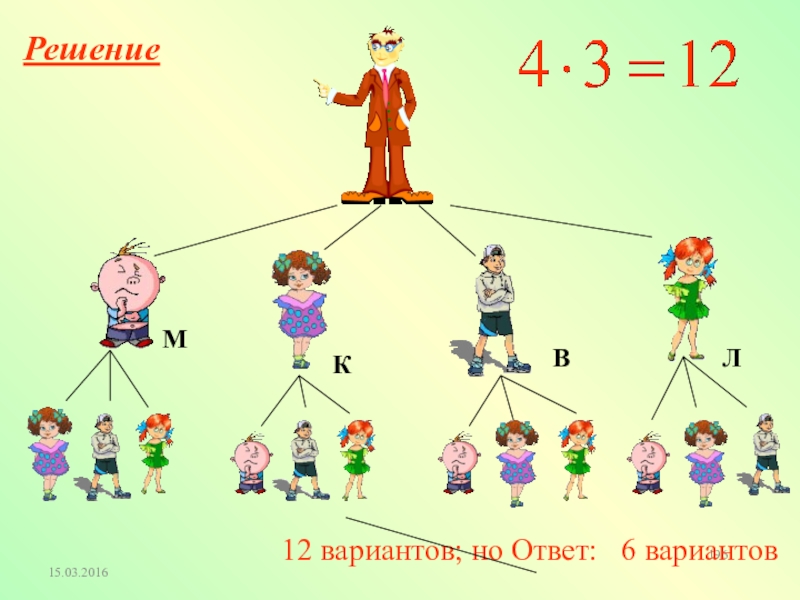
- 19. 612 вариантов; но Ответ: 6 вариантов РешениеМВКЛ
- 20. У Миши 4 ручки разного цвета и
- 21. 12 различных наборовмсбзчкс
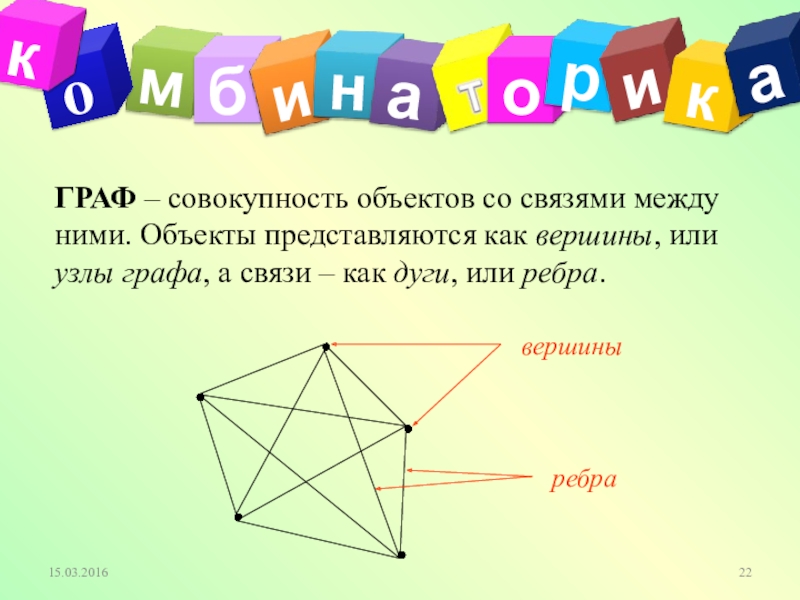
- 22. оГРАФ – совокупность объектов со связями между
- 23. Пятеро друзей встретились после каникул и обменялись
- 24. Сколько различных завтраков, состоящих из 1 напитка
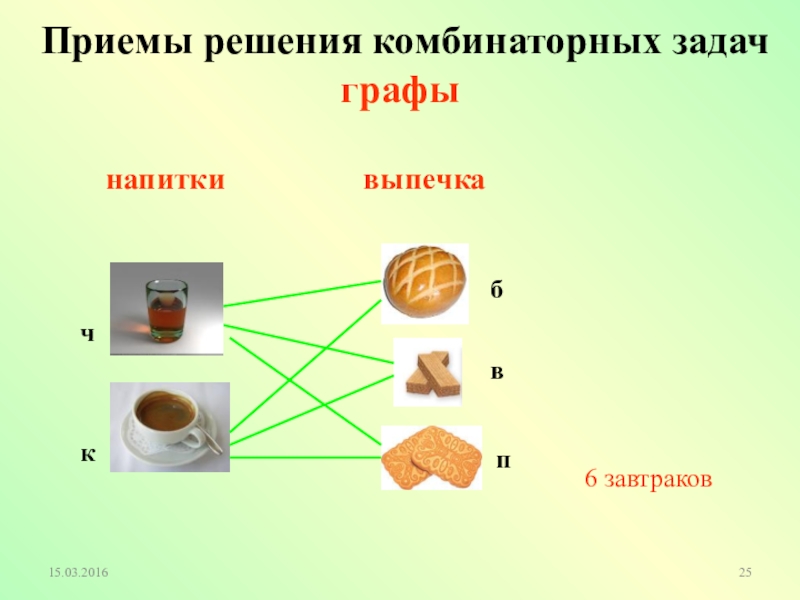
- 25. 6 завтраковнапиткивыпечкачкбпв Приемы решения комбинаторных задач графы
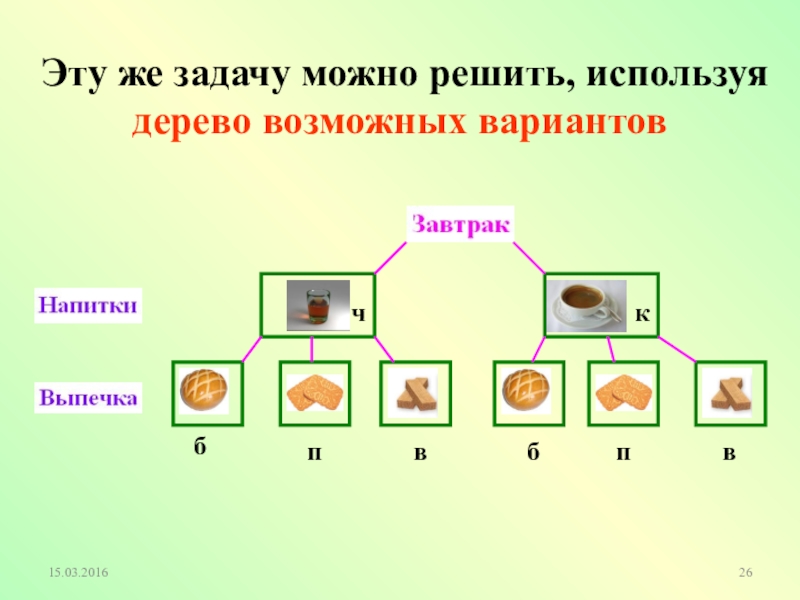
- 26. чкббппвв Эту же задачу можно решить, используя дерево возможных вариантов
- 27. ччччккккпппбббввв Решение задачи с помощью таблицы
- 28. Шесть семей уехали отдыхать в разные города.
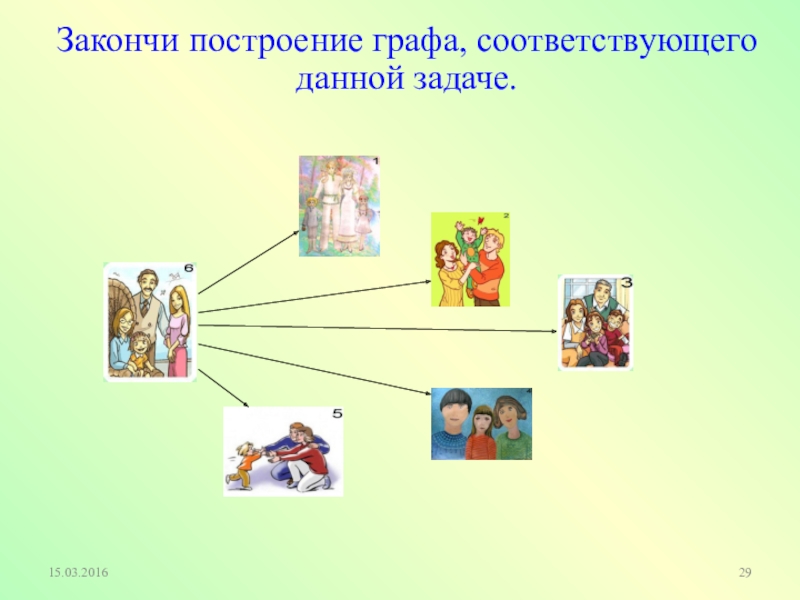
- 29. Закончи построение графа, соответствующего данной задаче.
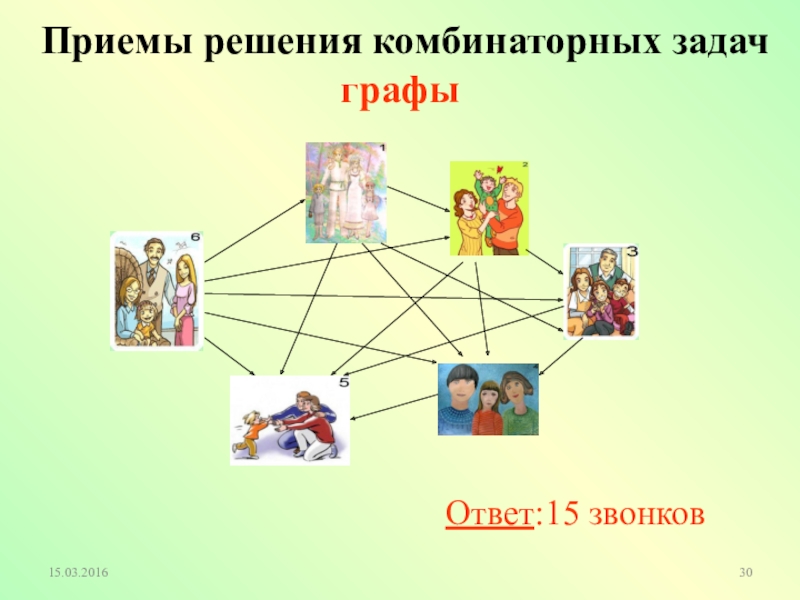
- 30. Приемы решения комбинаторных задач графыОтвет:15 звонков
- 31. –––––––––––––––––––––Ответ:15 звонков Приемы решения комбинаторных задач задачи, решаемые с помощью таблиц
- 32. Домашнее задание:п. 30№ 724(умножение), 720 (дерево), 726 (граф), 727 (таблица), 728 (перебор вариантов).
- 33. В магазине продают воздушные шары: красные, желтые,
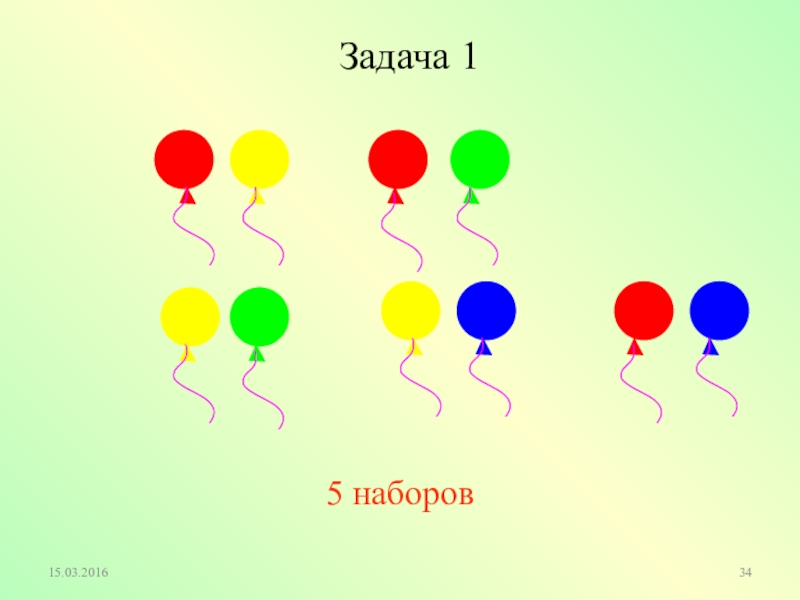
- 34. Задача 15 наборов
- 35. Приемы решения комбинаторных задач Задача 2В
- 36. Решение
- 37. В танцевальном кружке занимаются пять девочек: Женя,
- 38. Ответ: 25 парЖеняМашаКатяЮляДашаОлегВоваСтасАндрейИванОлегОлегОлегОлегОлегВоваВоваВоваВоваВоваСтасСтасСтасСтасСтасАндрейАндрейАндрейАндрейАндрейИванИванИванИванИванЖеняЖеняЖеняЖеняЖеняМашаМашаМашаМашаМашаКатяКатяКатяКатяКатяЮляЮляЮляЮляЮляДашаДашаДашаДашаДаша
- 39. Задачи, решаемые с помощью таблицНа завтрак
- 40. Существует много видов комбинаторных задач, это лишь некоторые из них.Спасибо за внимание!
Слайд 2Вопросы
Что такое комбинаторика?
От какого слова произошло слово «комбинаторика»?
Какие приемы решения
Слайд 3- раздел математики, в котором изучаются вопросы о том, сколько различных
о
Слайд 4Термин «комбинаторика» был введён в математический обиход немецким философом, математиком Лейбницем,
Термин «комбинаторика» происходит от латинского слова «combina», что в переводе на русский означает – «сочетать», «соединять».
Слайд 5Некоторые
приемы решения комбинаторных задач
решение методом перебора;
решение с помощью
решение с помощью комбинаторного правила умножения;
решение с помощью таблиц;
решение с помощью графов.
Слайд 6Люди, которые умело владеют техникой решения комбинаторных задач, а следовательно, обладают
Сейчас мы увидим, какими являетесь вы?
Слайд 7№715 (д\з)
У Ирины 5 подруг: Вера, Зоя, Марина, Полина и Светлана.
Замечание. При решении для краткости будем писать первые буквы имен.
Слайд 8Составим сначала все пары, в которые входит Вера.
ВЗ, ВМ, ВП,
Выпишем теперь пары, в которые входит Зоя, но не входит Вера.
Далее составим пары, в которые входит Марина, но не входят Вера и Зоя.
Еще одна пара
ЗМ, ЗП, ЗС
МП, МС
ПС
Всего существует 4+3+2+1=10
Решение
Ответ:10 вариантов
Вера
Зоя
Марина
Полина
Света
Получим 4 пары.
Таких пар три.
Их две.
Далее составим пары, в которые входит Полина.
Слайд 11Рассмотрим задачу. На цветочной клумбе сидели шмель, жук, бабочка и муха.
Способ рассуждений, которым мы воспользовались при решении задачи, называют перебором возможных вариантов.
ш
ж
б
м
Слайд 13 Таким образом, из
Ответ: 9 чисел.
Приемы решения комбинаторных задач
метод перебора
33;35;37; (начали с 3)
Решение: Для того, чтобы не пропустить и не повторить ни одного из чисел, будем выписывать их в порядке возрастания:
Сколько двузначных чисел можно составить, используя цифры 3; 5; 7?
53;55;57; (начали с 5)
73;75;77; (начали с 7)
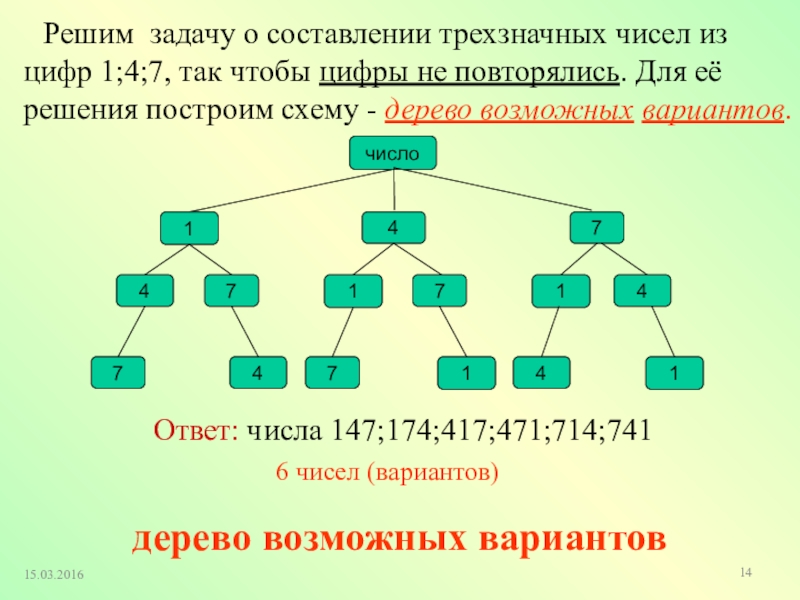
Слайд 14дерево возможных вариантов
Решим задачу о составлении трехзначных чисел из
число
1
4
7
4
4
7
7
1
1
7
7
1
1
4
4
Ответ: числа 147;174;417;471;714;741
6 чисел (вариантов)
Слайд 15
Заметим, что ответ на вопрос, можно получить, не выписывая
Первую цифру можно выбрать тремя способами. Так как после выбора первой цифры останутся две, то вторую цифру можно выбрать двумя способами. Остается приписать одну цифру. Следовательно, общее число искомых трехзначных чисел равно произведению
Слайд 16«Если объект А можно выбрать m способами, а другой объект В
Мы нашли ответ на вопрос, используя так называемое комбинаторное правило умножения
Слайд 17У Куклы Светы 3 юбки и 5 кофт, удачно сочетающихся по
Решение. 3·5 = 15
комбинаторное правило умножения
Слайд 18 Решите задачу, используя
дерево возможных вариантов
В класс пришли четыре новых
Л
В
К
М
Слайд 20У Миши 4 ручки разного цвета и 3 блокнота разного размера.
Приемы решения комбинаторных задач
задачи, решаемые с помощью таблиц
м
с
б
с
з
ч
к
Слайд 22о
ГРАФ – совокупность объектов со связями между ними. Объекты представляются как
вершины
ребра
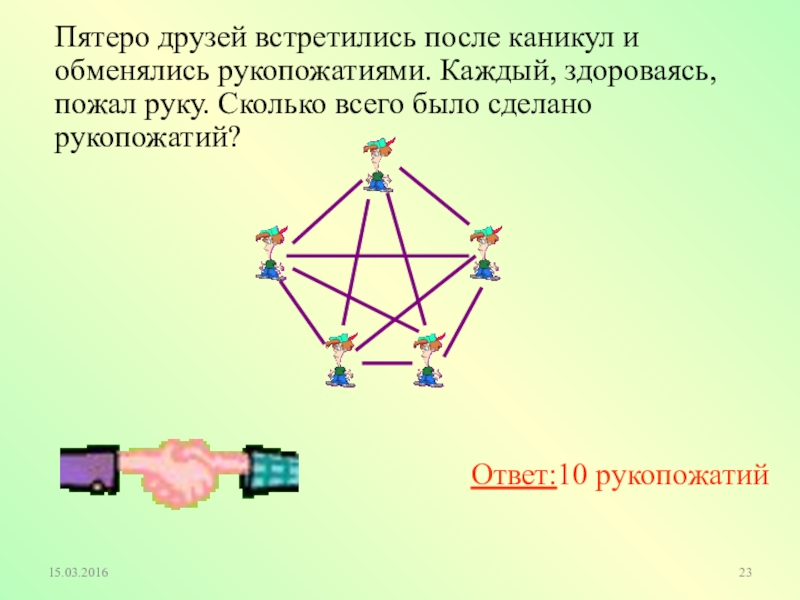
Слайд 23Пятеро друзей встретились после каникул и обменялись рукопожатиями. Каждый, здороваясь, пожал
Ответ:10 рукопожатий
Слайд 24Сколько различных завтраков, состоящих из 1 напитка и 1 вида выпечки,
Решите задачу, используя граф
ч
к
б
п
в
Слайд 28Шесть семей уехали отдыхать в разные города. Приехав к месту отдыха,
Решите задачу, используя граф
»
Слайд 31–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
Ответ:15 звонков
Приемы решения комбинаторных задач
задачи, решаемые с помощью таблиц
Слайд 32Домашнее задание:
п. 30
№ 724(умножение), 720 (дерево), 726 (граф), 727 (таблица), 728
Слайд 33В магазине продают воздушные шары: красные, желтые, зеленые, синие. Какие наборы
Задачи, решаемые
методом
организованного перебора
Приемы решения комбинаторных задач
дополнительные задачи
Задача 1
Слайд 35Приемы решения комбинаторных задач
Задача 2
В парке 4 пруда. Было решено
Задание: покажи, какие дорожки надо сделать.
Графы
Слайд 37В танцевальном кружке занимаются пять девочек: Женя, Маша, Катя, Юля и
Приемы решения комбинаторных задач
Задачи, решаемые
с помощью таблиц
Слайд 38Ответ: 25 пар
Женя
Маша
Катя
Юля
Даша
Олег
Вова
Стас
Андрей
Иван
Олег
Олег
Олег
Олег
Олег
Вова
Вова
Вова
Вова
Вова
Стас
Стас
Стас
Стас
Стас
Андрей
Андрей
Андрей
Андрей
Андрей
Иван
Иван
Иван
Иван
Иван
Женя
Женя
Женя
Женя
Женя
Маша
Маша
Маша
Маша
Маша
Катя
Катя
Катя
Катя
Катя
Юля
Юля
Юля
Юля
Юля
Даша
Даша
Даша
Даша
Даша
Слайд 39 Задачи, решаемые с помощью таблиц
На завтрак Миша может выбрать: плюшку,
Ответ:12 (4·3=12)