- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к итоговому уроку Решение простейших тригонометрических уравнений
Содержание
- 1. Презентация к итоговому уроку Решение простейших тригонометрических уравнений
- 2. Чтобы успешно решать простейшие тригонометрическиеуравнения необходимо следующее:
- 3. Дайте определение арккосинуса, арксинуса, арктангенса, арккотангенса. Назовите
- 4. Вычислить
- 5. Вычислить
- 6. Найти область допустимых значений выражения
- 7. Упростите выражение
- 8. Какие формулы мы используем для нахождения решений уравнений вида sinx=a, cosx=a, tgx=a, ctgx=a.Назовите частные решения.
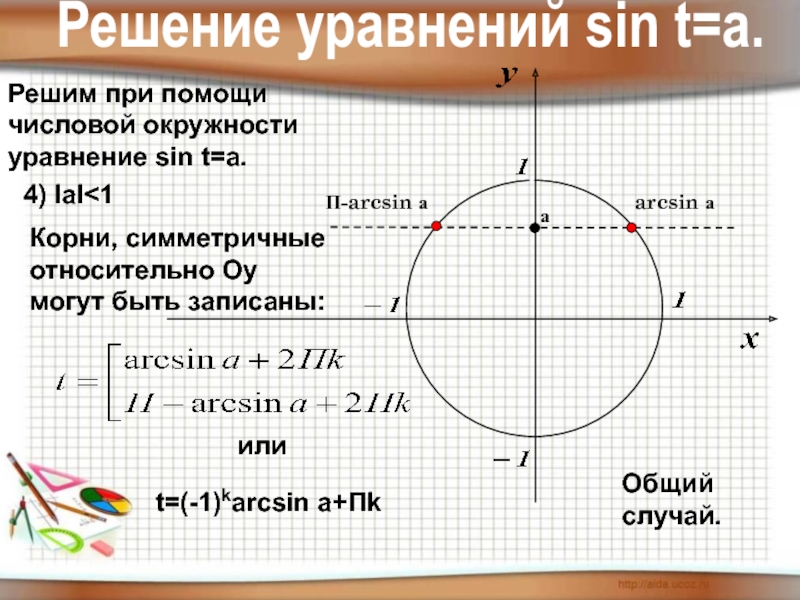
- 9. Решим при помощичисловой окружностиуравнение sin t=a. Решение уравнений sin t=a.4) IаI
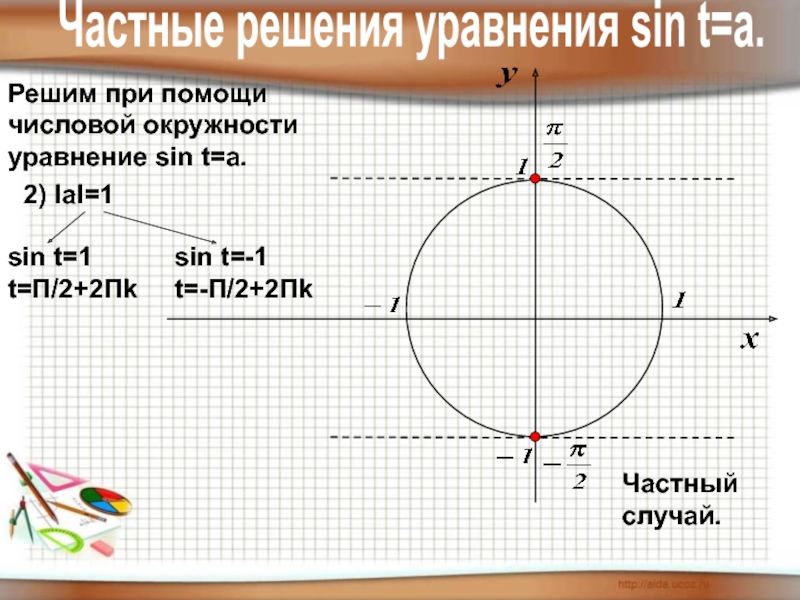
- 10. Решим при помощичисловой окружностиуравнение sin t=a.Частные решения уравнения sin t=a.2) IаI=1sin t=1t=П/2+2Пksin t=-1t=-П/2+2ПkЧастный случай.
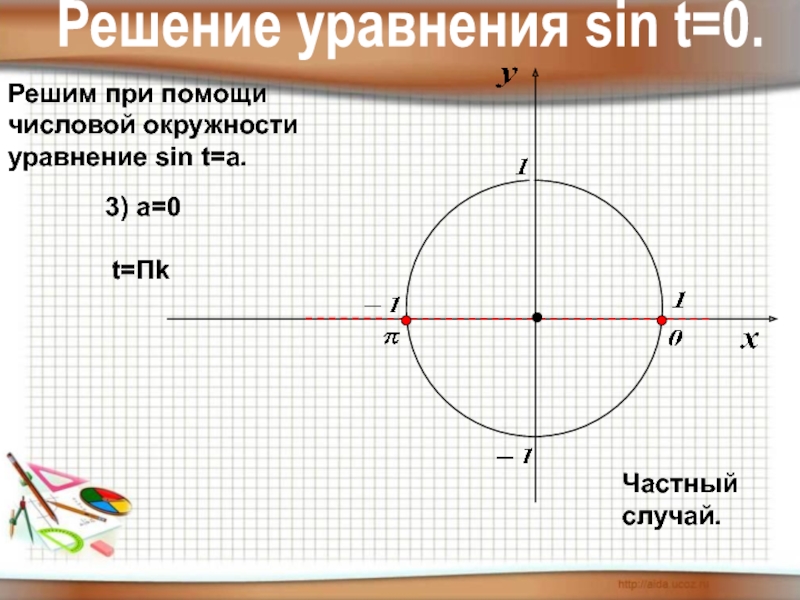
- 11. Решим при помощичисловой окружностиуравнение sin t=a. Решение уравнения sin t=0.3) а=0t=ПkЧастный случай.
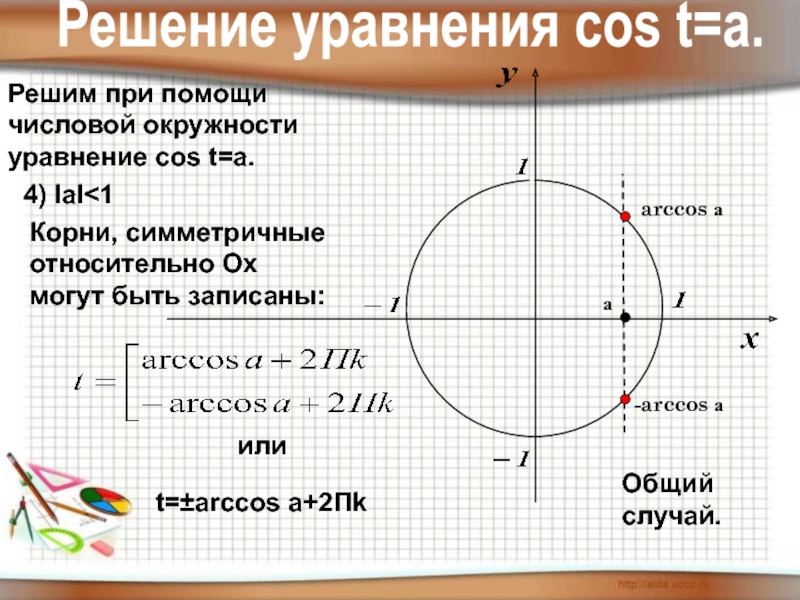
- 12. Решим при помощичисловой окружностиуравнение cos t=a.4) IаI
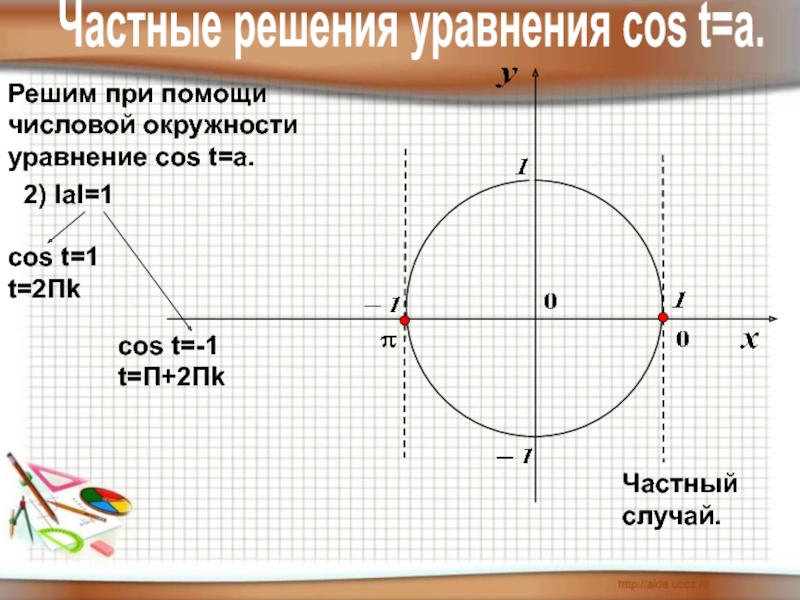
- 13. Решим при помощичисловой окружностиуравнение cos t=a.2) IаI=1cos t=1t=2Пkcos t=-1t=П+2ПkЧастный случай.Частные решения уравнения соs t=a.
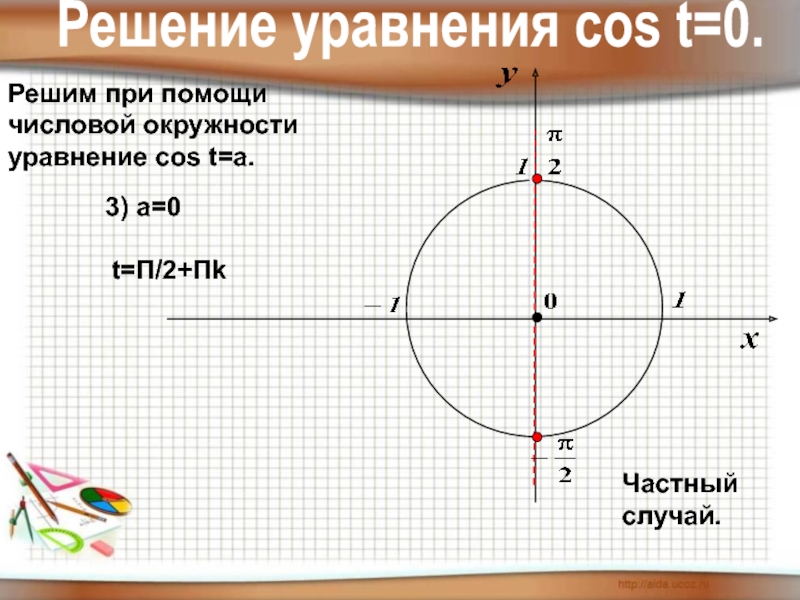
- 14. Решим при помощичисловой окружностиуравнение cos t=a.3) а=0t=П/2+ПkЧастный случай. Решение уравнения соs t=0.
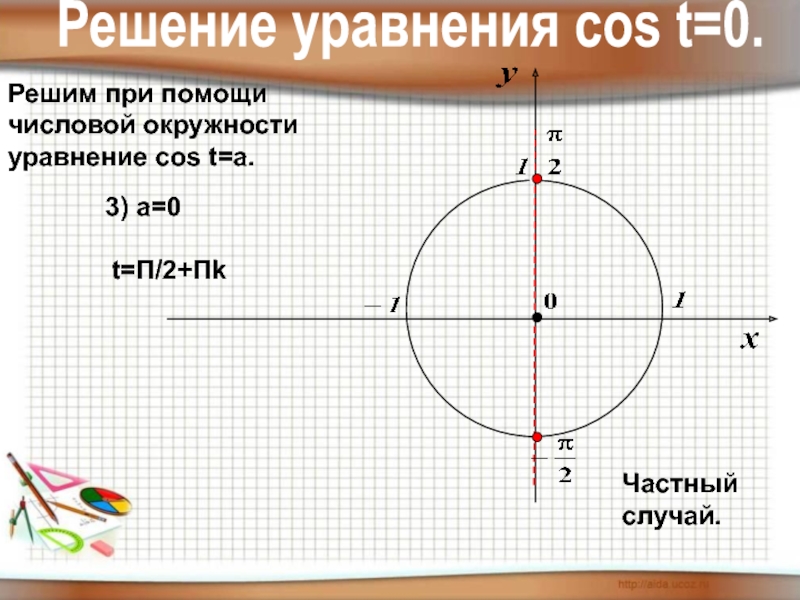
- 15. Решим при помощичисловой окружностиуравнение cos t=a.3) а=0t=П/2+ПkЧастный случай. Решение уравнения соs t=0.
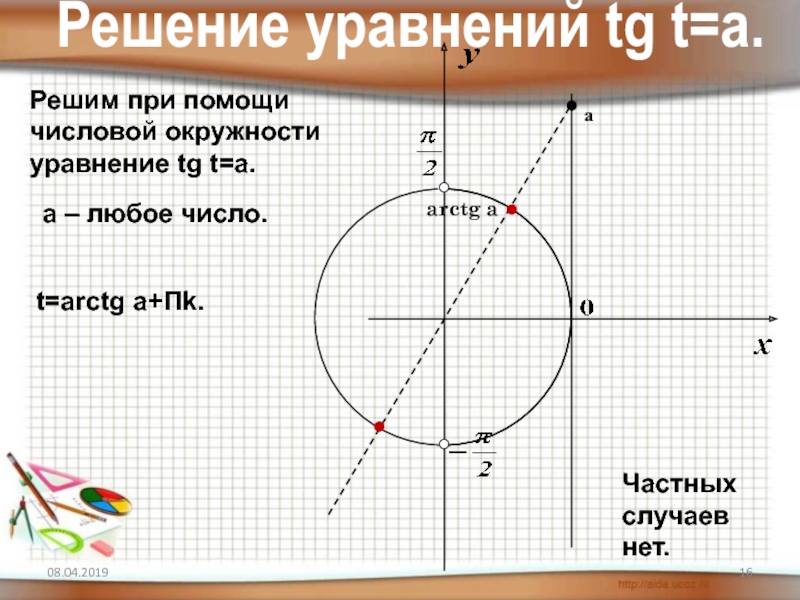
- 16. Решение уравнений tg t=a.Решим при помощичисловой
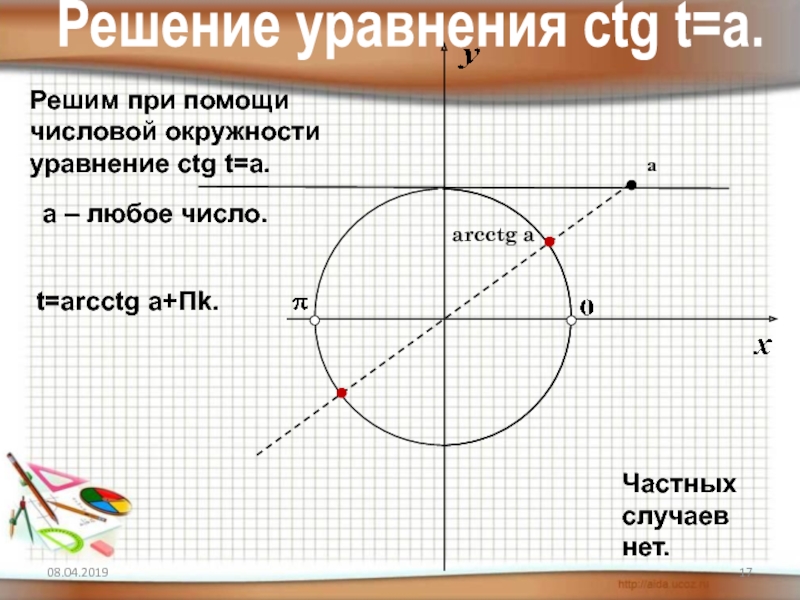
- 17. Решим при помощичисловой окружностиуравнение сtg t=a.arcctg aаa
- 18. Наша задача: свести любое тригонометрическое уравнение к простейшему виду.
- 19. Решите уравнения
- 20. Самостоятельная работа
- 21. Решите уравнения1 вариант2 вариант
- 22. Домашнее задание№_______,№_______
- 23. РефлексияЧто нового узнали на уроке? Испытывали ли
- 24. Спасибо за то, что стараешься!
Чтобы успешно решать простейшие тригонометрическиеуравнения необходимо следующее: 2) уметь определять значения синуса, косинуса, тангенса и котангенса для точек числовой окружности;4) знать понятие арксинуса, арккосинуса, арктангенса, арккотангенса и уметь отмечать их на числовой окружности.1) уметь отмечать точки
Слайд 1Решение простейших тригонометрических уравнений.
Исламова Зульфия Магсумовна
учитель математики
Слайд 2Чтобы успешно решать простейшие тригонометрические
уравнения необходимо следующее:
2) уметь определять значения
синуса, косинуса,
тангенса и котангенса для точек числовой
окружности;
тангенса и котангенса для точек числовой
окружности;
4) знать понятие арксинуса, арккосинуса,
арктангенса, арккотангенса и уметь отмечать их
на числовой окружности.
1) уметь отмечать точки на числовой
окружности;
3) знать свойства основных
тригонометрических функций;
Слайд 3Дайте определение арккосинуса, арксинуса, арктангенса, арккотангенса.
Назовите область определения и область
значений этих функций
Какая из функций является четной?
Какая из функций является четной?
Слайд 8Какие формулы мы используем для нахождения решений уравнений вида sinx=a, cosx=a,
tgx=a, ctgx=a.
Назовите частные решения.
Назовите частные решения.
Слайд 9Решим при помощи
числовой окружности
уравнение sin t=a.
Решение уравнений sin t=a.
4) IаI
случай.
arcsin а
П-arcsin а
Корни, симметричные относительно Оу могут быть записаны:
t=(-1)karcsin a+Пk
или
а
Слайд 10Решим при помощи
числовой окружности
уравнение sin t=a.
Частные решения уравнения sin t=a.
2) IаI=1
sin
t=1
t=П/2+2Пk
t=П/2+2Пk
sin t=-1
t=-П/2+2Пk
Частный случай.
Слайд 11Решим при помощи
числовой окружности
уравнение sin t=a.
Решение уравнения sin t=0.
3) а=0
t=Пk
Частный
случай.
Слайд 12Решим при помощи
числовой окружности
уравнение cos t=a.
4) IаI
относительно Оx могут быть записаны:
t=±arccos a+2Пk
или
а
Решение уравнения соs t=a.
Слайд 13Решим при помощи
числовой окружности
уравнение cos t=a.
2) IаI=1
cos t=1
t=2Пk
cos t=-1
t=П+2Пk
Частный случай.
Частные решения
уравнения соs t=a.
Слайд 14Решим при помощи
числовой окружности
уравнение cos t=a.
3) а=0
t=П/2+Пk
Частный случай.
Решение уравнения соs
t=0.
Слайд 15Решим при помощи
числовой окружности
уравнение cos t=a.
3) а=0
t=П/2+Пk
Частный случай.
Решение уравнения соs
t=0.
Слайд 16 Решение уравнений tg t=a.
Решим при помощи
числовой окружности
уравнение tg t=a.
arctg a
а
a
– любое число.
Частных случаев нет.
t=arctg a+Пk.
Слайд 17Решим при помощи
числовой окружности
уравнение сtg t=a.
arcctg a
а
a – любое число.
Частных случаев
нет.
t=arcctg a+Пk.
Решение уравнения сtg t=a.
Слайд 23Рефлексия
Что нового узнали на уроке?
Испытывали ли вы затруднения при выполнении
самостоятельной работы?
Какие из рассмотренных тригонометрических уравнений из оказались наиболее трудными?
Какие пробелы в знаниях выявились на уроке?
Какие проблемы у вас возникли по окончании урока?
Какие из рассмотренных тригонометрических уравнений из оказались наиболее трудными?
Какие пробелы в знаниях выявились на уроке?
Какие проблемы у вас возникли по окончании урока?
