СОШ
Шишигина Ю.В.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к докладу по теме: Развитие критического мышления на уроках математики (Описание опыта работы)
Содержание
- 1. Презентация к докладу по теме: Развитие критического мышления на уроках математики (Описание опыта работы)
- 2. «Учитель должен думать о том, чтобы сначала
- 3. «Кто не владеет техникой какого-нибудь искусства, науки,
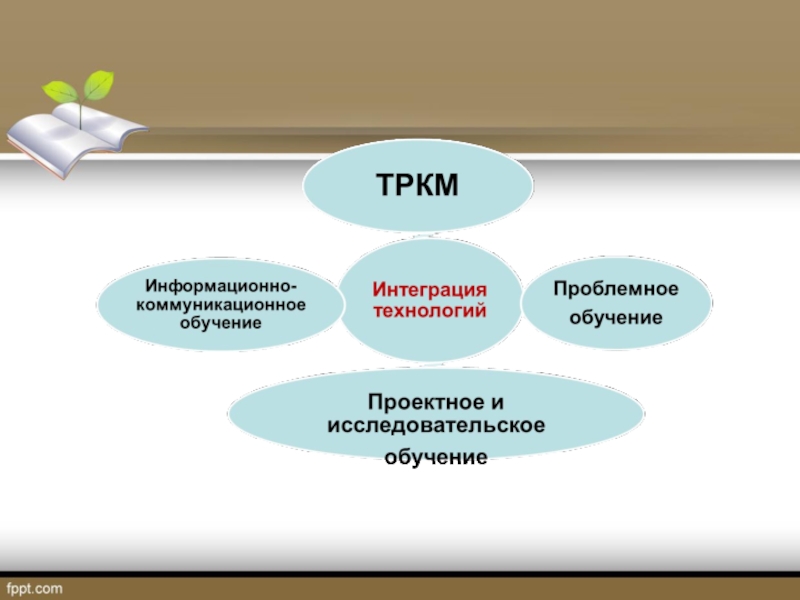
- 4. Системно-деятельностный подходКак учить?Обновление педагогических технологий
- 5. Какую технологию выбрать ведущей?
- 6. ТРКМ - технология развития критического мышления
- 7. Основная идея ТРКМСоздать такую атмосферу учения, при
- 8. Определение критического мышления:Во-первых, критическое мышление есть мышление
- 9. Основа ТРКМ –трехфазная структура урока:вызовосмыслениерефлексия
- 10. Функции трех фаз технологии развития критического мышления
- 11. Технологическая карта урока
- 12. Роль учителя в ТРКМ:направляю усилия учеников в
- 13. Ученик в ТРКМ учится:формировать собственное мнение;совершать обдуманный
- 14. Слайд 14
- 15. Основные приемы ТРКМ Таблица «толстых» и «тонких» вопросов
- 16. Ромашка БлумаПростой вопросУточняющий вопросОценочный вопросТворческий вопросВопрос интерпретацияПрактический вопрос?
- 17. Ромашка БлумаПростые вопросы (фактические вопросы) – требуют
- 18. Какие виды призм бывают?Какие фигуры могут лежать
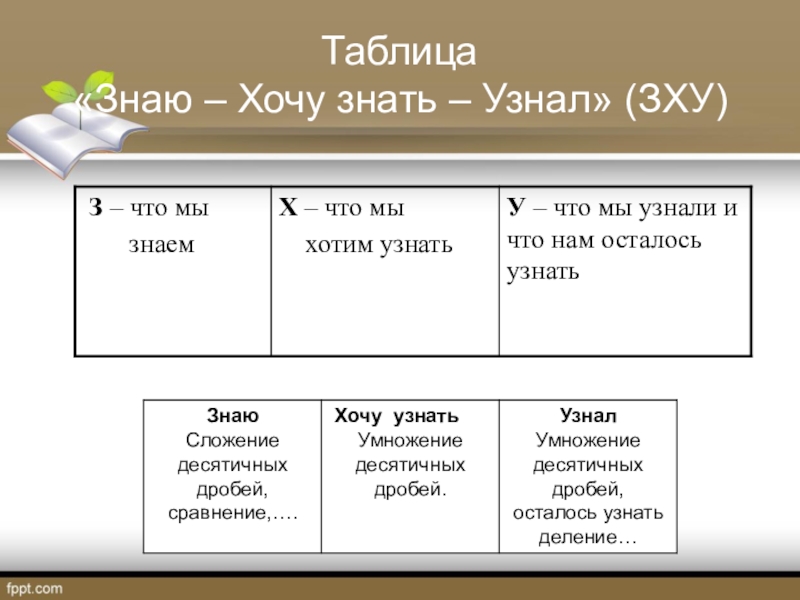
- 19. Таблица «Знаю – Хочу знать – Узнал» (ЗХУ)
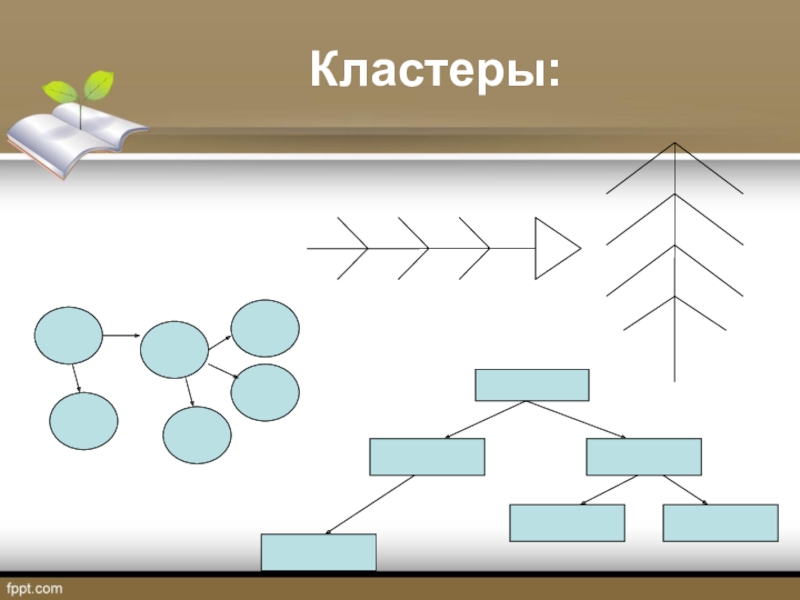
- 20. Кластеры:
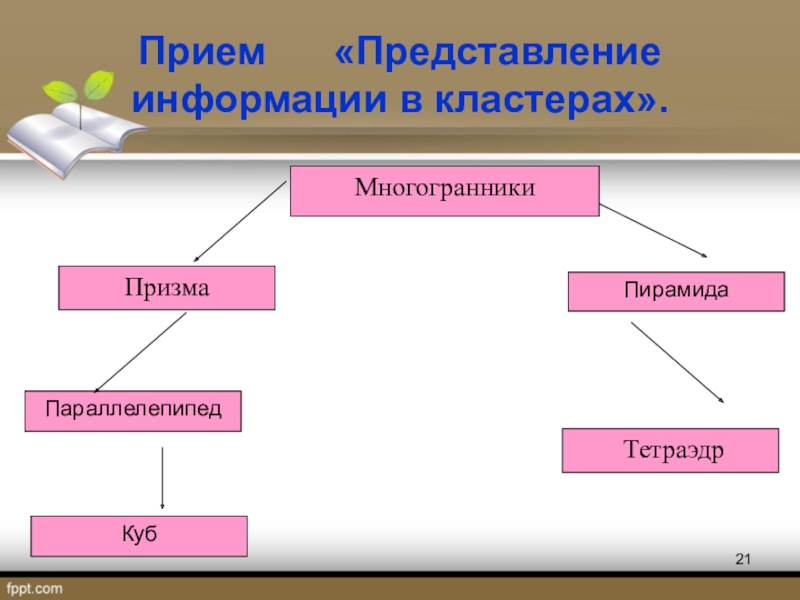
- 21. Прием «Представление информации в кластерах».
- 22. Слайд 22
- 23. Инсерт- маркировка текста значками по мере его
- 24. призмаМногогранник, две пары которого (основания) (+) –
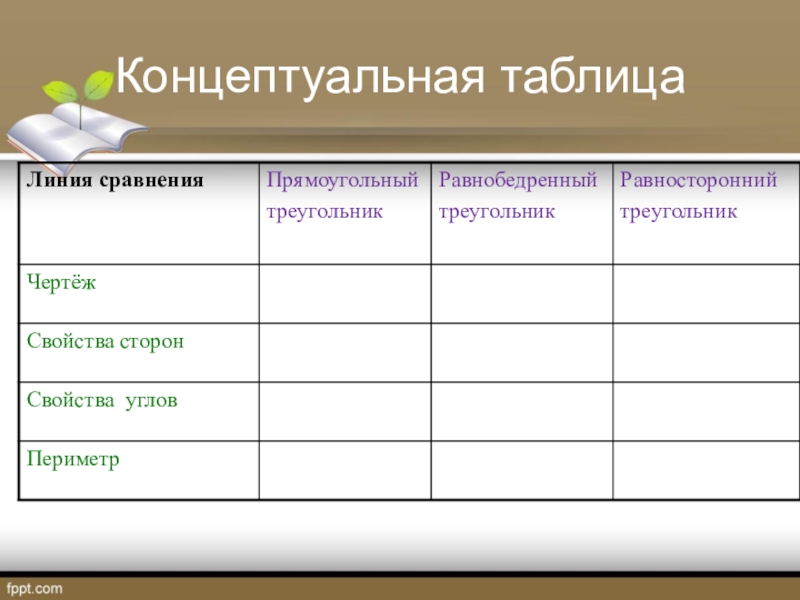
- 25. Концептуальная таблица
- 26. Концептуальная таблица
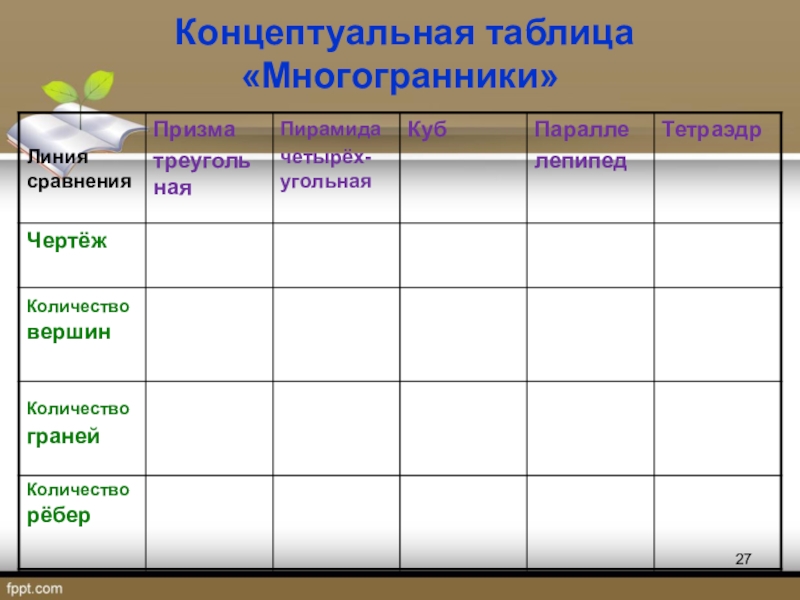
- 27. Концептуальная таблица «Многогранники»
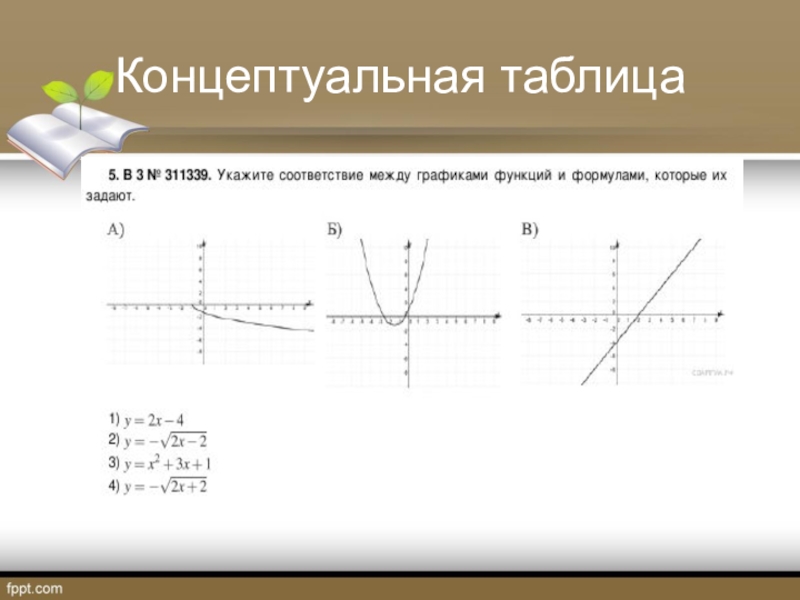
- 28. Концептуальная таблица
- 29. "Верные и неверные утверждения"
- 30. "Верные и неверные утверждения"
- 31. Прием «Составление «Синквейна»»Для его написания существуют правила:
- 32. МасштабАрифметический, географическийДелить,
- 33. Прием «Лови ошибку»Прием “Лови ошибку”Время выполнения: 5-6
- 34. Использование технологии развития критического мышления
- 35. Слайд 35
- 36. Список использованной литературыЗаир-Бек С., Муштавинская И. Развитие
- 37. СПАСИБО ЗА ВНИМАНИЕ!
«Учитель должен думать о том, чтобы сначала сделать ученика пригодным для восприятия образования. Учитель, прежде чем образовывать ученика своими наставлениями, сначала должен пробуждать в ученике стремление к образованию, делать ученика, по крайней мере, годным к образованию».
Слайд 1Развитие критического мышления на уроках математики
Выполнила: учитель математики и информатики
МБОУ Новотроицкой
Слайд 2«Учитель должен думать о том, чтобы сначала сделать ученика пригодным для
восприятия образования. Учитель, прежде чем образовывать ученика своими наставлениями, сначала должен пробуждать в ученике стремление к образованию, делать ученика, по крайней мере, годным к образованию».
Я.А. Коменский
Слайд 3
«Кто не владеет техникой какого-нибудь искусства, науки, ремесла, тот никогда не
будет способен создавать что-нибудь выдающееся»
И.В.Мичурин
И.В.Мичурин
Слайд 7Основная идея ТРКМ
Создать такую атмосферу учения, при которой учащиеся совместно с
учителем активно работают, сознательно размышляют над процессом обучения, отслеживают, подтверждают, опровергают или расширяют знания, новые идеи, чувства или мнения об окружающем мире.
Слайд 8Определение критического мышления:
Во-первых, критическое мышление есть мышление самостоятельное.
Во-вторых, информация является отправным,
а отнюдь не конечным пунктом критического мышления. Знание создает мотивировку, без которой человек не может мыслить критически.
В-третьих, критическое мышление начинается с постановки вопросов и уяснения проблем, которые нужно решить.
В-четвертых, критическое мышление стремится к убедительной аргументации.
В-пятых, критическое мышление есть мышление социальное. (Дэвид Клустер, США)
В-третьих, критическое мышление начинается с постановки вопросов и уяснения проблем, которые нужно решить.
В-четвертых, критическое мышление стремится к убедительной аргументации.
В-пятых, критическое мышление есть мышление социальное. (Дэвид Клустер, США)
Слайд 12Роль учителя в ТРКМ:
направляю усилия учеников в определенное русло;
сталкиваю различные суждения;
создаю
условия, побуждающие к принятию самостоятельных решений;
даю учащимся возможность самостоятельно делать выводы;
подготавливаю новые познавательные ситуации внутри уже существующих.
даю учащимся возможность самостоятельно делать выводы;
подготавливаю новые познавательные ситуации внутри уже существующих.
Слайд 13Ученик в ТРКМ учится:
формировать собственное мнение;
совершать обдуманный выбор между различными мнениями;
решать
проблемы;
аргументировано спорить;
ценить совместную работу, в которой возникает общее решение;
уметь оценить чужую точку зрения и сознавать, что восприятие человека и его отношение к любому вопросу формируется под влиянием многих факторов.
аргументировано спорить;
ценить совместную работу, в которой возникает общее решение;
уметь оценить чужую точку зрения и сознавать, что восприятие человека и его отношение к любому вопросу формируется под влиянием многих факторов.
Слайд 16Ромашка Блума
Простой
вопрос
Уточняющий
вопрос
Оценочный
вопрос
Творческий
вопрос
Вопрос
интерпретация
Практический
вопрос
?
Слайд 17Ромашка Блума
Простые вопросы (фактические вопросы) – требуют знания фактического материала, ориентированы
на работу памяти
Уточняющие вопросы (на понимание) – «насколько я понял….», «правильно ли я Вас поняла, что…»
Интерпретирующие вопросы (объясняющие) – «объясните почему…»
Оценочные вопросы (сравнение) – «сравните это…»
Творческие вопросы (прогноз) – «Как вы думаете, что произойдет, если…?»
Практические вопросы – «Как мы можем…?»
Уточняющие вопросы (на понимание) – «насколько я понял….», «правильно ли я Вас поняла, что…»
Интерпретирующие вопросы (объясняющие) – «объясните почему…»
Оценочные вопросы (сравнение) – «сравните это…»
Творческие вопросы (прогноз) – «Как вы думаете, что произойдет, если…?»
Практические вопросы – «Как мы можем…?»
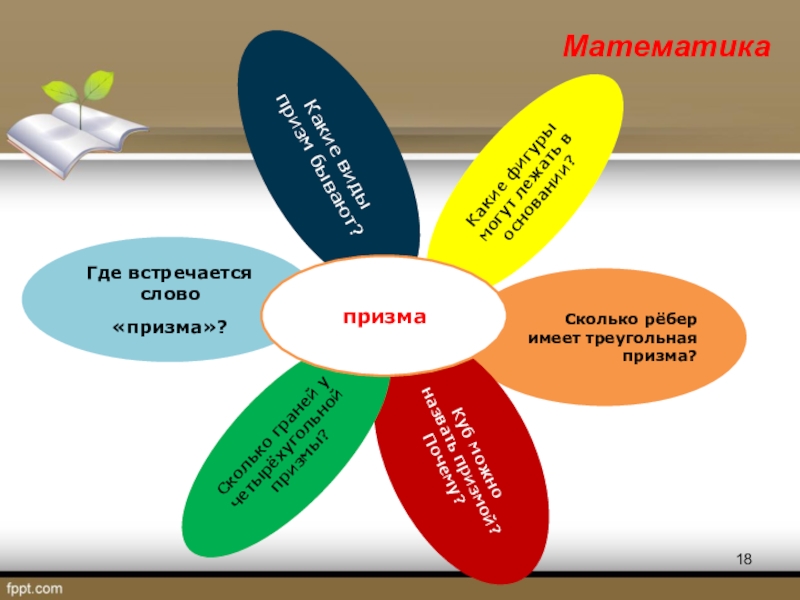
Слайд 18Какие виды призм бывают?
Какие фигуры могут лежать в основании?
Сколько рёбер имеет
треугольная призма?
Куб можно назвать призмой? Почему?
Сколько граней у четырёхугольной призмы?
Где встречается слово
«призма»?
призма
Математика
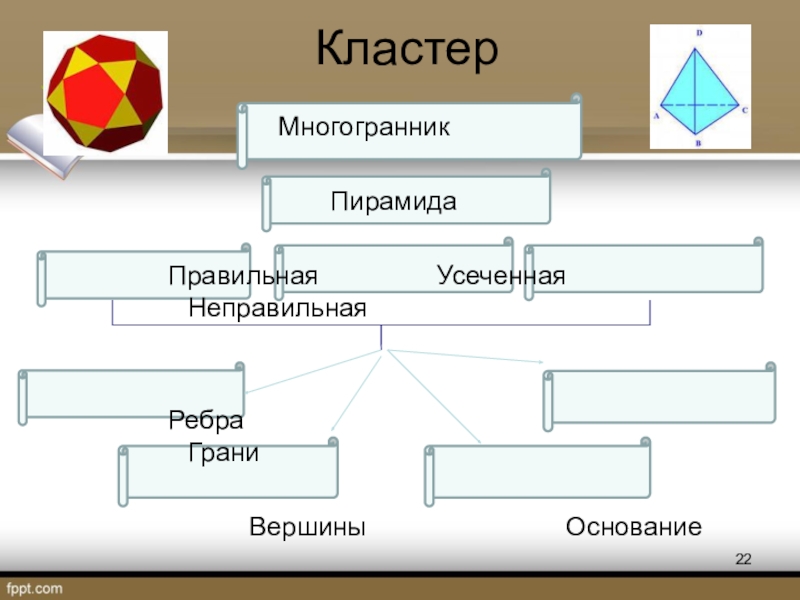
Слайд 22
Многогранник
Пирамида
Правильная Усеченная Неправильная
Ребра Грани
Вершины Основание
Кластер
Слайд 23
Инсерт- маркировка текста значками по мере его чтения.
«v» - уже знал
«+»
- новое
«-» - думал иначе
«?» - не понял, есть вопросы
«-» - думал иначе
«?» - не понял, есть вопросы
Слайд 24призма
Многогранник, две пары которого (основания) (+) – равные n-угольники, лежащие в
параллельных плоскостях(v), а остальные n граней – параллелограммы (боковые грани) (+). Стороны боковых граней, не лежащие на основаниях, называются боковыми ребрами. (-) Призму можно рассматривать как результат параллельного переноса основания вдоль некоторого отрезка (ребра). (?)
Слайд 32Масштаб
Арифметический, географический
Делить,
находить, вычислять
Дробь, которую нужно понять
Отношение
Дробь, которую нужно понять
Отношение
:
Слайд 33Прием «Лови ошибку»
Прием “Лови ошибку”
Время выполнения: 5-6 минут
Описание приема.
Учитель заранее подготавливает
текст, содержащий ошибочную информацию, и предлагает учащимся выявить допущенные ошибки.
Важно, чтобы задание содержало в себе ошибки 2 уровней:
А – явные, которые достаточно легко выявляются учащимися, исходя из их личного опыта и знаний;
Б - скрытые, которые можно установить, только изучив новый материал.
Учащиеся анализируют предложенный текст, пытаются выявить ошибки, аргументируют свои выводы.
Учитель предлагает изучить новый материал, после чего вернуться к тексту задания и исправить те ошибки, которые не удалось выявить в начале урока.
Важно, чтобы задание содержало в себе ошибки 2 уровней:
А – явные, которые достаточно легко выявляются учащимися, исходя из их личного опыта и знаний;
Б - скрытые, которые можно установить, только изучив новый материал.
Учащиеся анализируют предложенный текст, пытаются выявить ошибки, аргументируют свои выводы.
Учитель предлагает изучить новый материал, после чего вернуться к тексту задания и исправить те ошибки, которые не удалось выявить в начале урока.
Слайд 34 Использование технологии развития критического мышления на уроках математики
Технологию
развития критического мышления необходимо применять на уроках математики, так как она:
развивает мыслительную деятельность учащихся;
формирует умение аргументировано высказываться,
задавать разумные вопросы, делать логические умозаключения .
Методы и приёмы технологии способствуют:
лучшему запоминанию изученного материала;
активизируют деятельность учащихся на уроке;
формулирование вопросов развивает познавательную деятельность.
Различные формы рефлексии развивают:
способность формулировать мысли;
помогают лучше понять причины явлений.
развивает мыслительную деятельность учащихся;
формирует умение аргументировано высказываться,
задавать разумные вопросы, делать логические умозаключения .
Методы и приёмы технологии способствуют:
лучшему запоминанию изученного материала;
активизируют деятельность учащихся на уроке;
формулирование вопросов развивает познавательную деятельность.
Различные формы рефлексии развивают:
способность формулировать мысли;
помогают лучше понять причины явлений.
Слайд 36Список использованной литературы
Заир-Бек С., Муштавинская И. Развитие критического мышления на уроке.
Пособие для учителя. – М., 2004.
Клустер Д. Что такое критическое мышление // Русский язык. 2002. № 29. С. 3
Критическое мышление: технология развития: Пособие для учителя / И. О. Загашев, С. И. Заир-Бек. – СПб: Альянс «Дельта», 2003.
4. Дьюи Д. Демократия и образование. — М., 2000. — С. 138— 144.
Халперн Д,. Психология критического мышления. — СПб., 2000.
Полат Е. С. Современные педагогические и информационные технологии в системе образования : учеб. пособие для студентов высш. учеб. заведений / Е.С. Полат, М. Ю. Бухаркина. — М. : Издательский центр «Академия», 2007. — 368 с.
Клустер Д. Что такое критическое мышление // Русский язык. 2002. № 29. С. 3
Критическое мышление: технология развития: Пособие для учителя / И. О. Загашев, С. И. Заир-Бек. – СПб: Альянс «Дельта», 2003.
4. Дьюи Д. Демократия и образование. — М., 2000. — С. 138— 144.
Халперн Д,. Психология критического мышления. — СПб., 2000.
Полат Е. С. Современные педагогические и информационные технологии в системе образования : учеб. пособие для студентов высш. учеб. заведений / Е.С. Полат, М. Ю. Бухаркина. — М. : Издательский центр «Академия», 2007. — 368 с.