Исследовательская работа по алгебре
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад исследовательской работы Тайна числа ПИ8 класс
Содержание
- 1. Презентация исследовательской работы Тайна числа ПИ8 класс
- 2. Задачи:1) Дать определение числа π2) Выяснить историю
- 3. Гипотеза:Число «Пи» - самое таинственное и интересное из всех чисел
- 4. Гордый Рим трубил победу Над твердыней
- 5. Число π — математическая константа, выражающая отношение
- 6. Первая тысяча знаков приближённого значения числа «ПИ» :3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861045432664821339360726024914127372458700660631558817488152092096282925409171536436789259036001133053054882046652138414695194151160943305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194912983367336244065664308602139494639522473719070217986094370277053921717629317675238467481846766940513200056812714526356082778577134275778960917363717872146844090122495343014654958537105079227968925892354201995611212902196086403441815981362977477130996051870721134999999837297804995105973173281609631859502445945534690830264252230825334468503526193118817101000313783875288658753320838142061717766914730359825349042875546873115956286388235378759375195778185778053217122680661300192787661119590921642019
- 7. Интересные фактыНеофициальный праздник «День числа Пи» отмечается
- 8. История числа πПроблеме π – 4000 лет.
- 9. =3,1605Папирус АХМЕСА2000 до н.э.В знаменитом папирусе Ахмеса
- 10. В Вавилоне в v веке до н.
- 11. Архимед ( III в. до н. э.)
- 12. Индусы в V-VIв. пользовались числом √10≈3,1611, а
- 13. В XV в. иранский математик Ал-Каши нашел
- 14. Андриан Ван Ромен (Бельгия) в XVI
- 15. Обозначение π (первая буква в греческом
- 16. π — иррациональное число, то есть его
- 17. Проведём практическую работу.Возьмём 3 любых предметов: стакан, кружку, баночку.
- 18. Обвяжем предметы ниткой и таким образом мы измерим длину окружности.
- 19. Измерим диаметр предмета
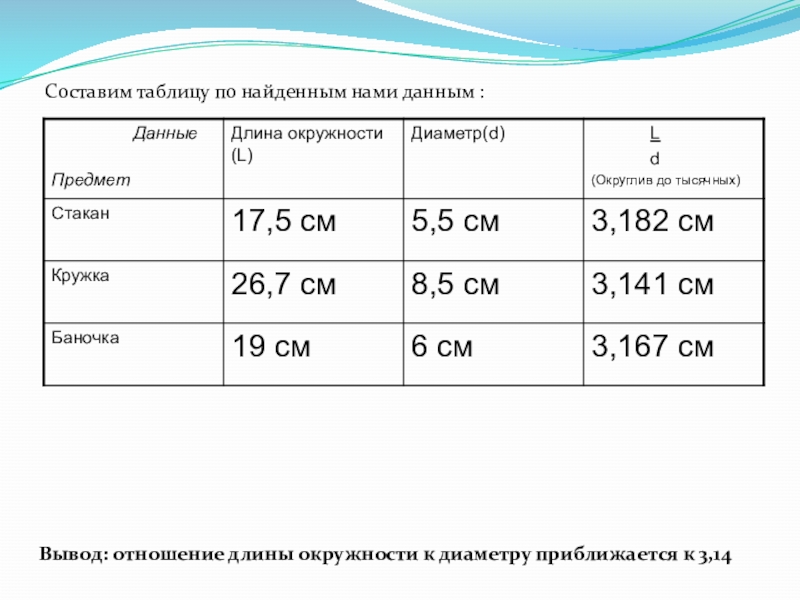
- 20. Составим таблицу по найденным нами данным :Вывод: отношение длины окружности к диаметру приближается к 3,14
- 21. Опыт Жоржа Бюффонаπ = Где n-число
- 22. О вычислениях значения числа π на современном
- 23. С помощью компьютера было вычислено десятичных знаков:1949
- 24. В 2009 году французский программист Фабрис Беллар
- 25. Вывод:Мы хотели узнать об истории вычисления числа
- 26. Источники информации:Б.А. Кордемский «Математические завлекалки».А.В. Жуков «Вездесущее
Слайд 1
Тайна числа π
Выполнили : ученицы 8 класса
Цибина Карина, Чепурина Анна
Руководитель
Слайд 2Задачи:
1) Дать определение числа π
2) Выяснить историю вычисления π.
3) Провести эксперимент
4)Провести опыт Бюффона.
5) Рассмотреть некоторые факты из «современной биографии» числа π. .
На историческом материале показать важность проблемы вычисления числа π, раскрыть необходимость точных вычислений значения π на современном этапе, а также показать огромное трудолюбие и работоспособность учёных, занимавшихся этим вопросом в течение многих столетий.
Цели:
Слайд 4 Гордый Рим трубил победу Над твердыней Сиракуз; Но трудами Архимеда Много больше я
шесть!
С.Бобров
Памятник числу «пи» на ступенях перед зданием Музея искусств в Сиэтле
Слайд 5Число π — математическая константа, выражающая отношение длины окружности к длине
Если принять диаметр окружности за единицу, то длина окружности и есть число π.
В цифровом выражении π начинается как 3,141592 и имеет бесконечную математическую продолжительность.
Определение
Слайд 6 Первая тысяча знаков приближённого значения числа «ПИ» :
3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861045432664821339360726024914127372458700660631558817488152092096282925409171536436789259036001133053054882046652138414695194151160943305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194912983367336244065664308602139494639522473719070217986094370277053921717629317675238467481846766940513200056812714526356082778577134275778960917363717872146844090122495343014654958537105079227968925892354201995611212902196086403441815981362977477130996051870721134999999837297804995105973173281609631859502445945534690830264252230825334468503526193118817101000313783875288658753320838142061717766914730359825349042875546873115956286388235378759375195778185778053217122680661300192787661119590921642019
Слайд 7Интересные факты
Неофициальный праздник «День числа Пи» отмечается 14 марта, которое в
Ещё одной датой, связанной с числом π, является 22 июля, которое называется «Днём приближённого числа Пи», так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби является приближённым значением числа π.
В штате Юта (США) был принят закон с очень короткой формулировкой "Пи равно трем", а в штате Индиана властями было официально назначено, что Пи равно 4.
Слайд 8История числа π
Проблеме π – 4000 лет. Исследователи древних пирамид установили,
Слайд 9=3,1605
Папирус АХМЕСА
2000 до н.э.
В знаменитом папирусе Ахмеса приводится такое указание для
« Отбрось от диаметра его девятую часть и
построй квадрат со стороной, равной остальной части, будет он эквивалентен кругу»
Из этого следует, что у Ахмеса π ≈ 3,1605.
Так началась письменная история числа π:
Слайд 10В Вавилоне в v веке до н. э. пользовались числом 3
а в древней Греции числом (√2+√3)≈3,1462643.
В индийских «сутрах» VI–V в до н. э. имеются правила, из которых вытекает, что π ≈3,008.
Наиболее древняя формулировка нахождения приближённого значения отношения длины окружности к диаметру содержится в стихах индийского математика Ариабхаты (V-VI в)
Прибавь четыре к сотне и умножь на восемь,
Потом ещё шестьдесят две тысячи прибавь.
Когда поделишь результат на двадцать тысяч,
Тогда откроется тебе значение
Длины окружности к двум радиусам отношенья, т. е.
длина окружности 62832
__________________ = ______ ≈3,1416
диаметр 20000
Слайд 11Архимед ( III в. до н. э.) для оценки числа π
Такой метод вычисления длины окружности посредством периметров вписанных и описанных многоугольников применялся многими видными математиками на протяжении почти 2000 лет.
10 1
Архимед получил 3 ---- < π < 3 ---- ,
т. е. π≈ 3, 1418. 71 7
Долгое время все пользовались значением
числа, равным
22
----
7
Слайд 12Индусы в V-VIв. пользовались
числом √10≈3,1611,
а китайцы –
числом ------- ≈ 3, 1415927;
113
Это значение записывалось в виде именованного числа:
3 ЧЖАНА 1 ЧИ 4 ЦУНЯ 1 ФЕНЬ 5 ЛИ 9 ХАО 2 ТЯО 7 ХО.
Слайд 13В XV в. иранский математик Ал-Каши нашел значение π с 16-ю
3*228 сторонами.
=3,141592653589793
Слайд 14Андриан Ван Ромен (Бельгия) в XVI получил 17 верных десятичных
Согласно завещанию, на его надгробном камне было высечено найденное им значение π.
Слайд 15 Обозначение π (первая буква в греческом слове окружность, периферия) впервые
а после опубликования работы Леонарда Эйлера (1736г. С.-Петербург), вычислившего значение π с точностью до 153 десятичных знаков, обозначение π становится общепринятым.
Слайд 16π — иррациональное число, то есть его значение не может быть
π — трансцендентное число, это означает, что оно не может быть корнем какого-либо многочлена с целыми коэффициентами. Трансцендентность числа π была доказана в 1882 году профессором Кенигсбергского, а позже Мюнхенского университета Линдеманом. Доказательство упростил Феликс Клейн в 1894 году.
Слайд 20Составим таблицу по найденным нами данным :
Вывод: отношение длины окружности к
Слайд 21Опыт Жоржа Бюффона
π =
Где n-число бросков иглы, m-число пересечений
между прямыми в 2 раза больше длины иглы.
=
= 3,125
Слайд 22О вычислениях значения числа π на современном этапе
С появлением ЭВМ значения
Вычисление такого числа знаков для π не имеет практического значения, а лишь показывает огромное преимущество и совершенство современных средств и методов вычисления по сравнению со старыми.
Слайд 23С помощью компьютера было вычислено десятичных знаков:
1949 год — 2037 десятичных
1958 год — 10000 десятичных знаков
1961 год — 100000 десятичных знаков
1973 год — 10000000 десятичных знаков
1986 год — 29360000 десятичных знаков
1987 год — 134217000 десятичных знаков
1989 год — 1011196691 десятичный знак
1991 год — 2260000000 десятичных знаков
1994 год — 4044000000 десятичных знаков
1995 год — 4294967286 десятичных знаков
1997 год — 51539600000 десятичных знаков
1999 год — 206 158 430 000 десятичных знаков.
Суперкомпьютер в сентябре 1999 года работал 37 часов 21 минут 4 секунды, используя 865 Гбайт памяти для основной задачи, и 46 часов и 816 Гбайт для вспомогательной оптимизации вычислений.
Слайд 24В 2009 году французский программист Фабрис Беллар поставил рекорд вычисления числа
Слайд 25Вывод:
Мы хотели узнать об истории вычисления числа Пи, и думаем, что
Точное значение числа Пи в современном мире представляет собой не только собственную научную ценность, но и используется для очень точных вычислений (например, орбиты спутника, строительства гигантских мостов), а также оценки быстродействия и мощности современных компьютеров.
Слайд 26Источники информации:
Б.А. Кордемский «Математические завлекалки».
А.В. Жуков «Вездесущее число пи»
Балк М. Математика
http://dic.academic.ru/dic.nsf/ruwiki/2244
http://ru.wikipedia.org/wiki/Pi
http://arbuz.narod.ru/z_piclub.htm