- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Графики тригонометрических функций
Содержание
- 1. Презентация Графики тригонометрических функций
- 2. Вспомним определение синуса и косинуса угла поворота:sinαcosα
- 3. 00ππxxyy011α1α2α3α3α2α11Масштаб π:3α4α4α5α5α6α6На оси абсцисс координатной плоскости Оху
- 4. 0πxy1Масштаб π:3Таким образом, мы получили график функции
- 5. xy0101Напомним некоторые рациональные значения функции у=sinx на промежутке [−π; π]:−1
- 6. xy10Масштаб π:3На практике, для построения графика функции
- 7. xy10Масштаб π:3−1Используя равенство cosx=sin(
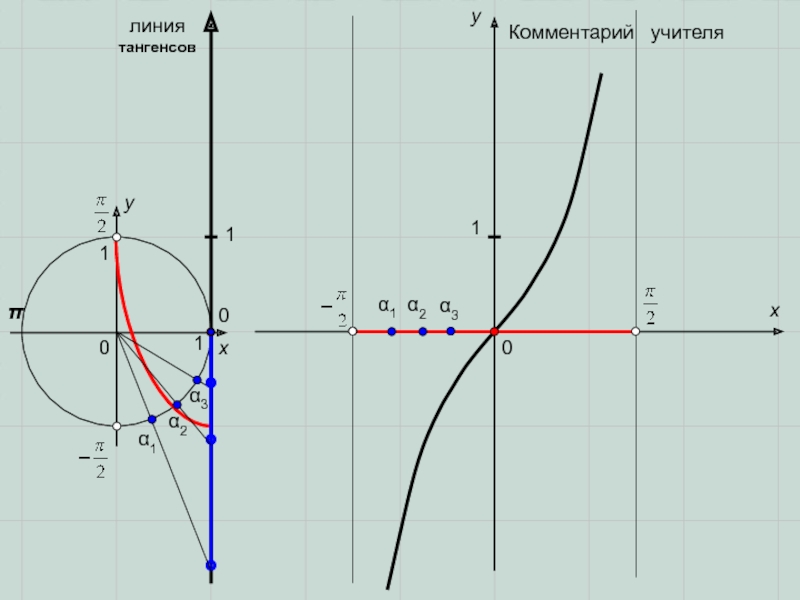
- 8. 00πxxyy011α1α2α3α3α2α11линия тангенсов1Комментарий учителя
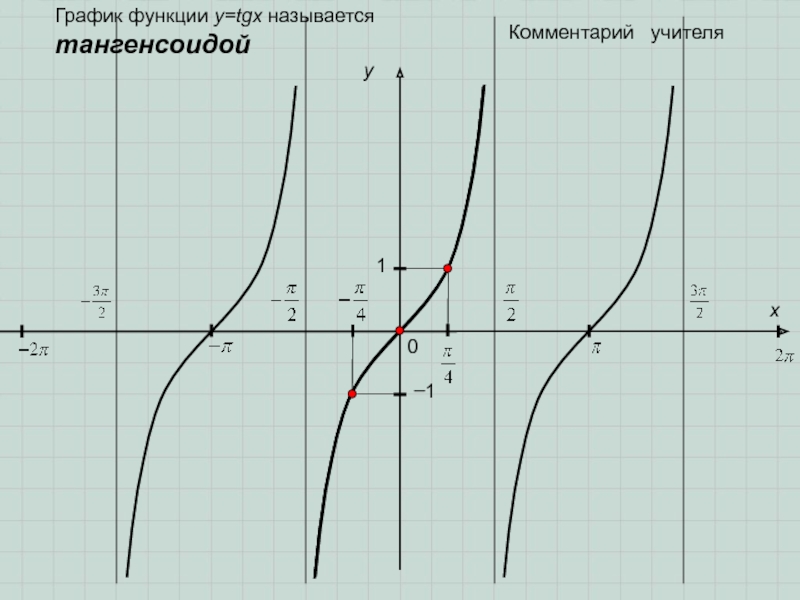
- 9. 0y1x−1Комментарий учителяГрафик функции y=tgx называется тангенсоидой
- 10. 0y1x−1Комментарий учителяМасштаб π:3
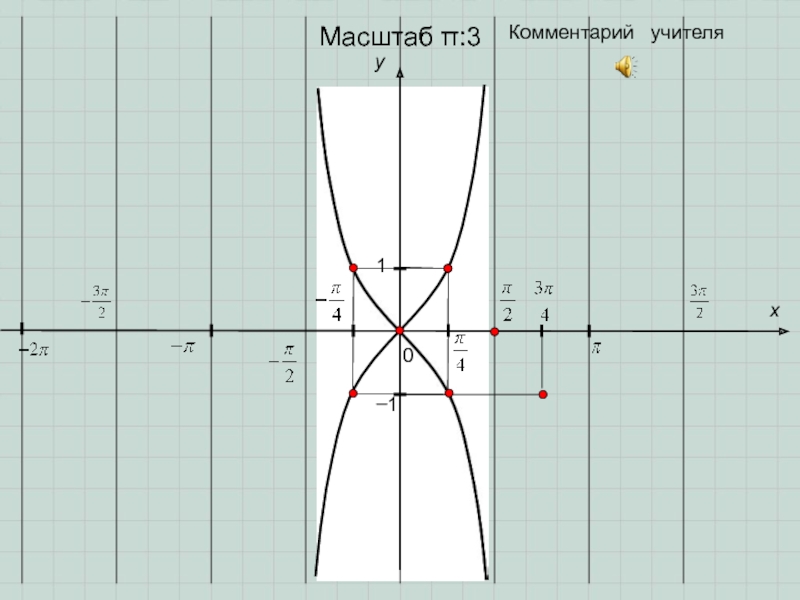
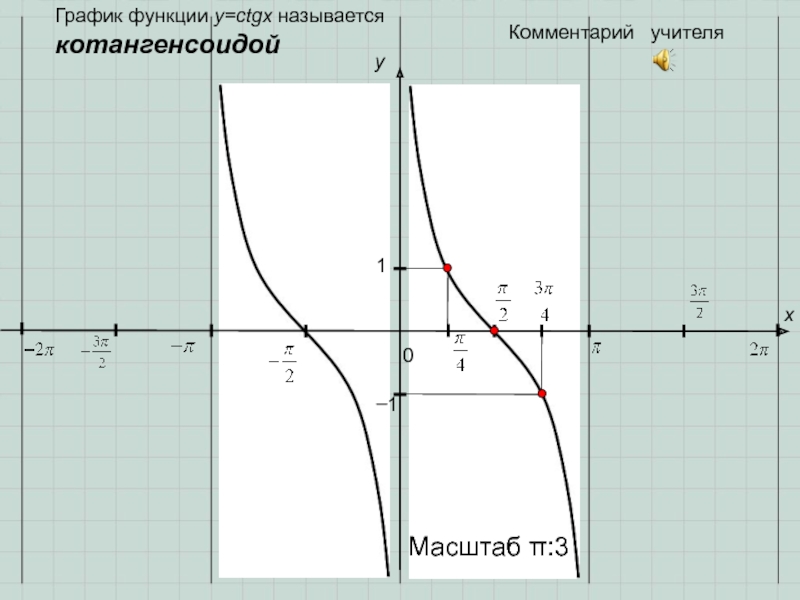
- 11. 0y1x−1Комментарий учителяГрафик функции y=ctgx называется котангенсоидойМасштаб π:3
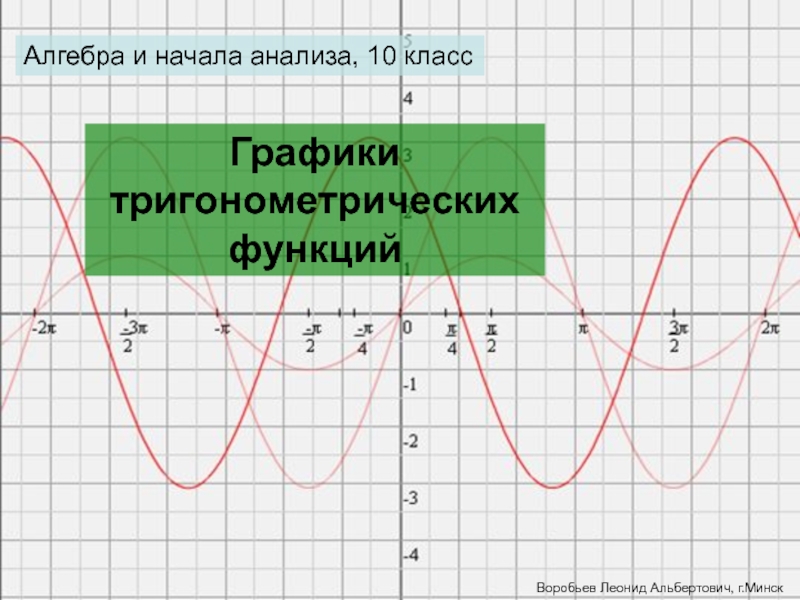
Слайд 1Алгебра и начала анализа, 10 класс
Графики тригонометрических функций
Воробьев Леонид Альбертович, г.Минск
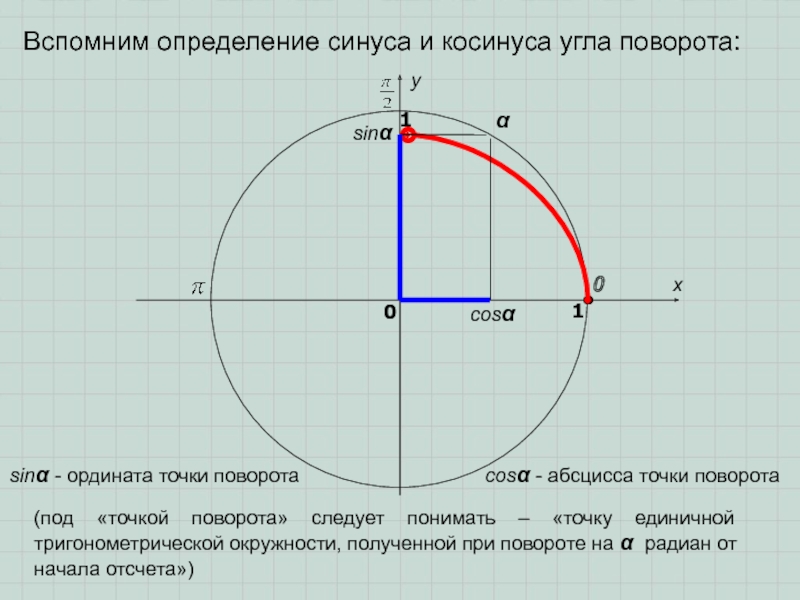
Слайд 2Вспомним определение синуса и косинуса угла поворота:
sinα
cosα
α
x
y
0
1
0
1
sinα - ордината точки
cosα - абсцисса точки поворота
(под «точкой поворота» следует понимать – «точку единичной тригонометрической окружности, полученной при повороте на α радиан от начала отсчета»)
Слайд 3
0
0
π
π
x
x
y
y
0
1
1
α1
α2
α3
α3
α2
α1
1
Масштаб π:3
α4
α4
α5
α5
α6
α6
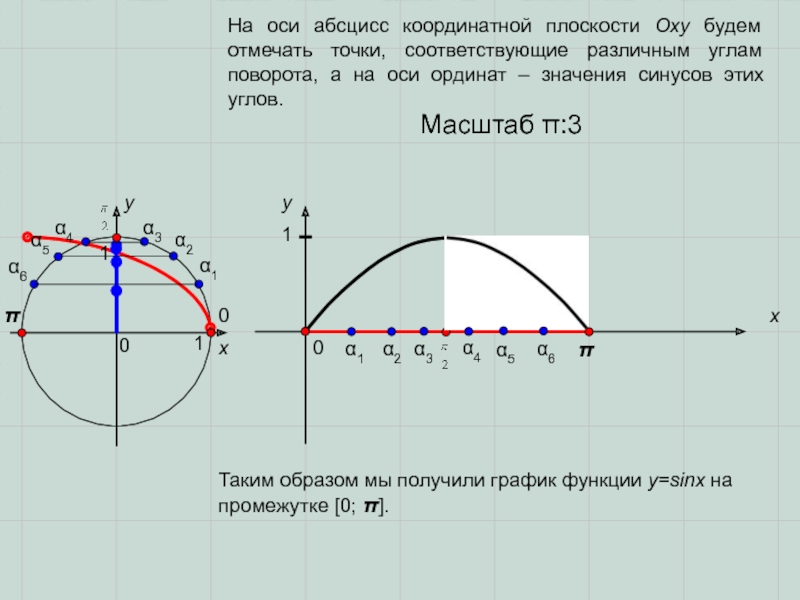
На оси абсцисс координатной плоскости Оху будем отмечать точки, соответствующие
Таким образом мы получили график функции y=sinx на промежутке [0; π].
Слайд 40
π
x
y
1
Масштаб π:3
Таким образом, мы получили график функции y=sinx на промежутке [−π
−1
−π
Теперь воспользуемся тем, что функция y=sinx является нечетной, а, значит, график функции на промежутке [−π ; 0] можно получить из данного симметрией относительно начала координат (или поворотом на 1800).
Слайд 6x
y
1
0
Масштаб π:3
На практике, для построения графика функции у=sinx на промежутке [0;
После этого используют свойство периодичности функции у=sinx. Так как наименьший положительный период функции y=sinx равен 2π, то изображенный участок графика можно параллельно переносить влево и вправо вдоль оси Ох на 2π⋅n (n∈) единичных отрезков.
−1
График функции y=sinx называется синусоидой.
Слайд 7x
y
1
0
Масштаб π:3
−1
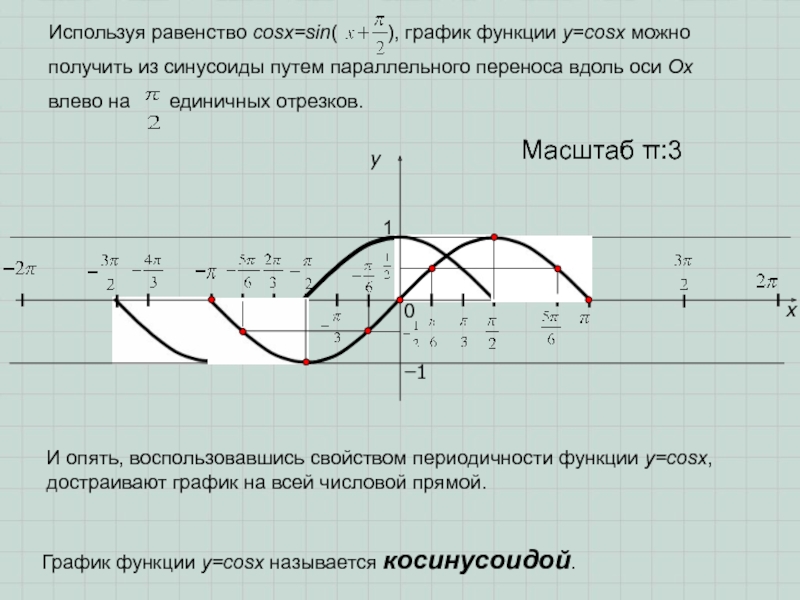
Используя равенство cosx=sin( ), график функции
получить из синусоиды путем параллельного переноса вдоль оси Ох
влево на единичных отрезков.
И опять, воспользовавшись свойством периодичности функции y=cosx, достраивают график на всей числовой прямой.
График функции y=cosx называется косинусоидой.
![Презентация Графики тригонометрических функций 0πxy1Масштаб π:3Таким образом, мы получили график функции y=sinx на промежутке [−π 0πxy1Масштаб π:3Таким образом, мы получили график функции y=sinx на промежутке [−π ; π].−1−πТеперь воспользуемся тем, что функция](/img/thumbs/a585cef66d859b12d37c2d15c7e6febb-800x.jpg)
![Презентация Графики тригонометрических функций xy0101Напомним некоторые рациональные значения функции у=sinx на промежутке [−π; π]:−1 xy0101Напомним некоторые рациональные значения функции у=sinx на промежутке [−π; π]:−1](/img/thumbs/b0985d544e61896c9c73992d55dcb210-800x.jpg)
![Презентация Графики тригонометрических функций xy10Масштаб π:3На практике, для построения графика функции у=sinx на промежутке [0; xy10Масштаб π:3На практике, для построения графика функции у=sinx на промежутке [0; π], сначала отмечают точки с координатами](/img/thumbs/bb6afce5a27b100d099959f6bb27a3c6-800x.jpg)