их свойства и графики
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре и началам анализа на тему Тригонометрические функции
Содержание
- 1. Презентация по алгебре и началам анализа на тему Тригонометрические функции
- 2. [-3;5]0ху7-51Подумай!2[-5;7)3[-5;7]Подумай!4(-3;5]Подумай!Проверка Найдите область определения функции, график
- 3. Найдите множество значений функции,
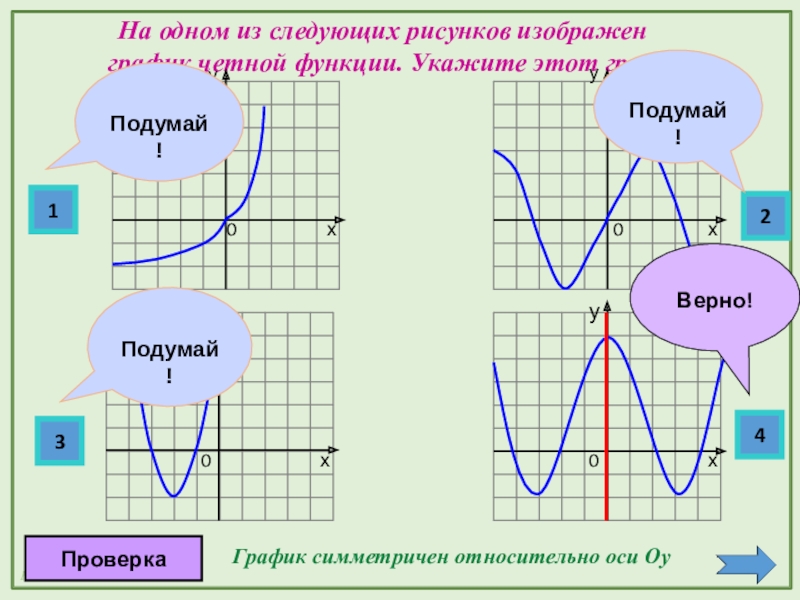
- 4. На одном из следующих рисунков изображен
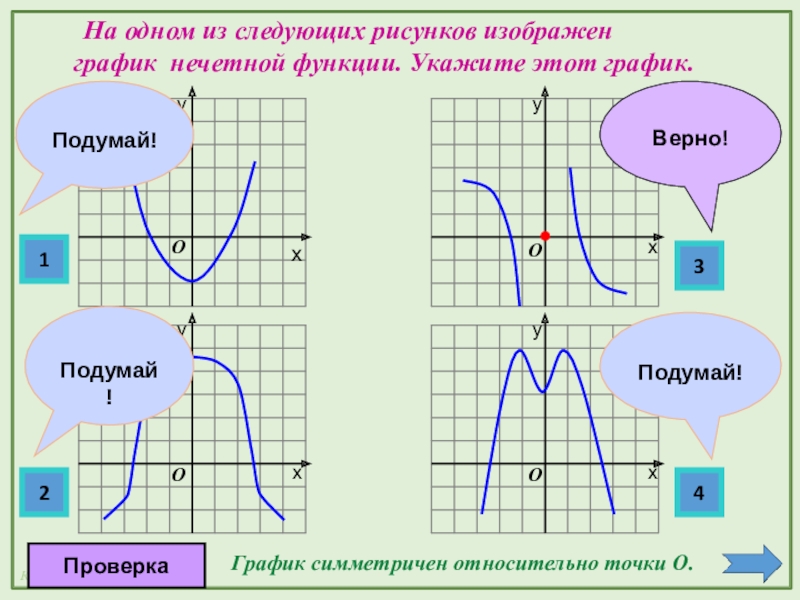
- 5. 1234ххххуууу На одном из следующих рисунков изображен
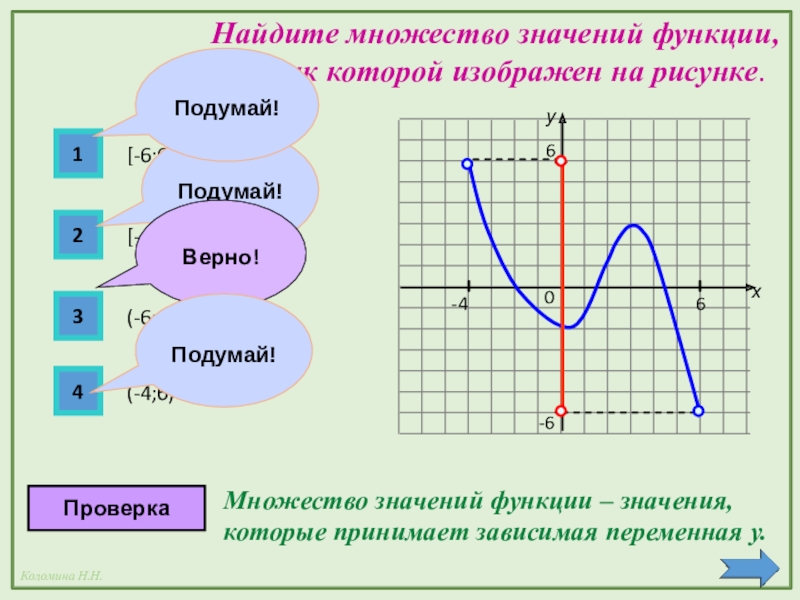
- 6. 1234[-6;7][-5;-3] U [2;6][-3;7][-3;2]Проверках026-57-3-6Подумай!Подумай!-23Подумай ! На рисунке изображен
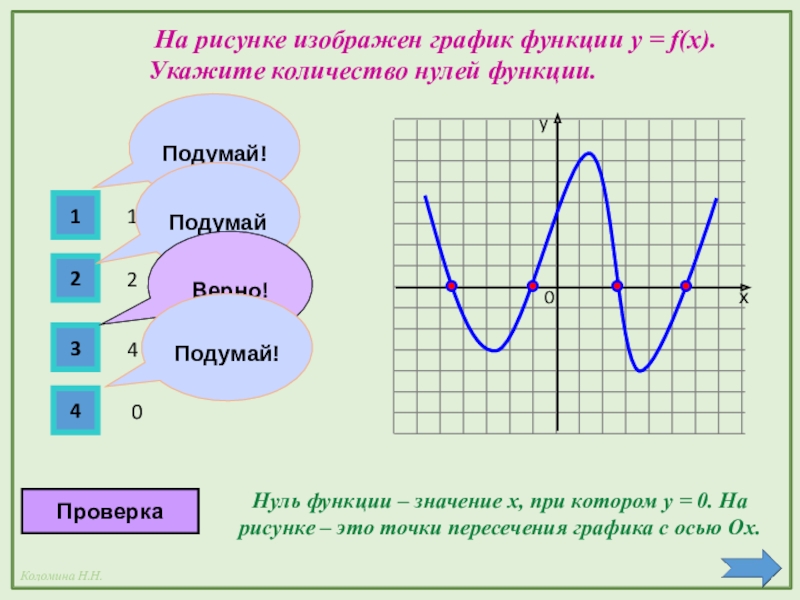
- 7. yх12341240Подумай!Подумай!Верно!Подумай!ПроверкаНуль функции – значение х, при котором
- 8. Для каждой функции выберите соответствующий ей периодФункция:Вариант ответа:
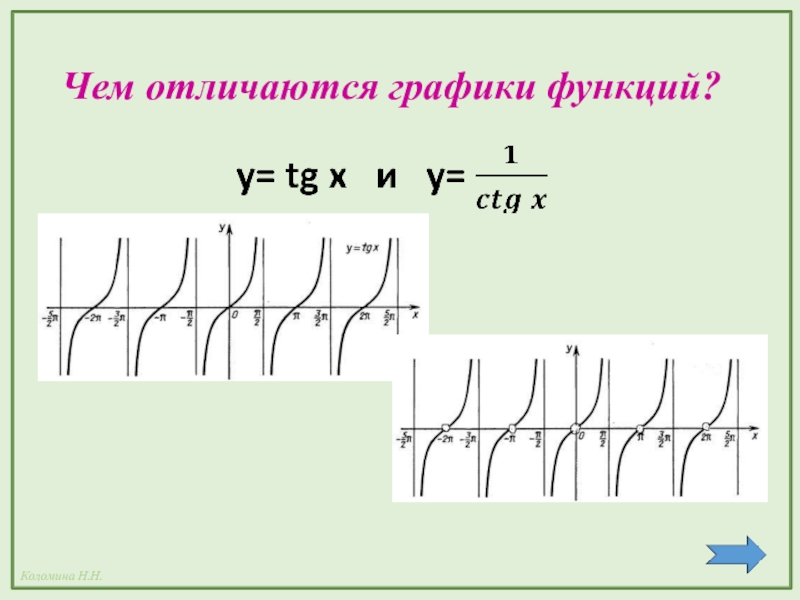
- 9. Чем отличаются графики функций?
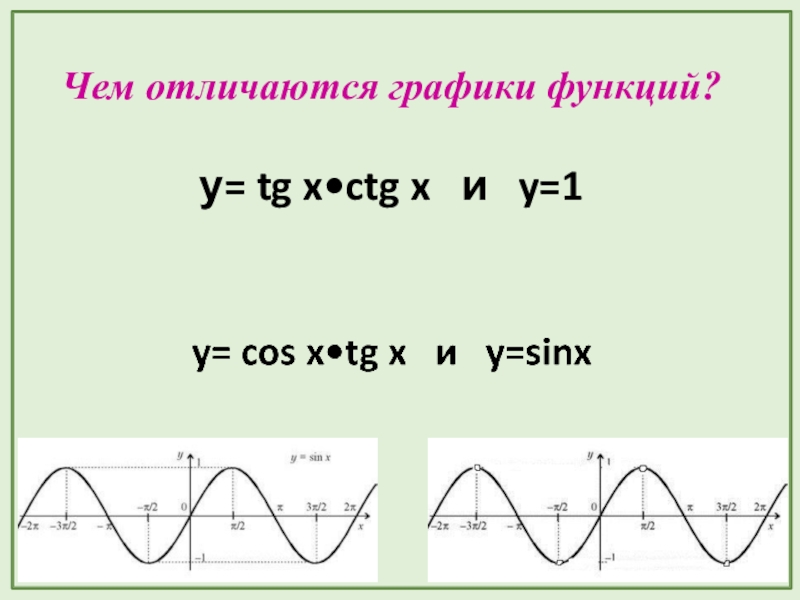
- 10. Чем отличаются графики функций?у= tg x•ctg x и y=1
- 11. Работа в группахКаждой группе определен свой цвет. Необходимо выполнить задание соответствующего цвета.
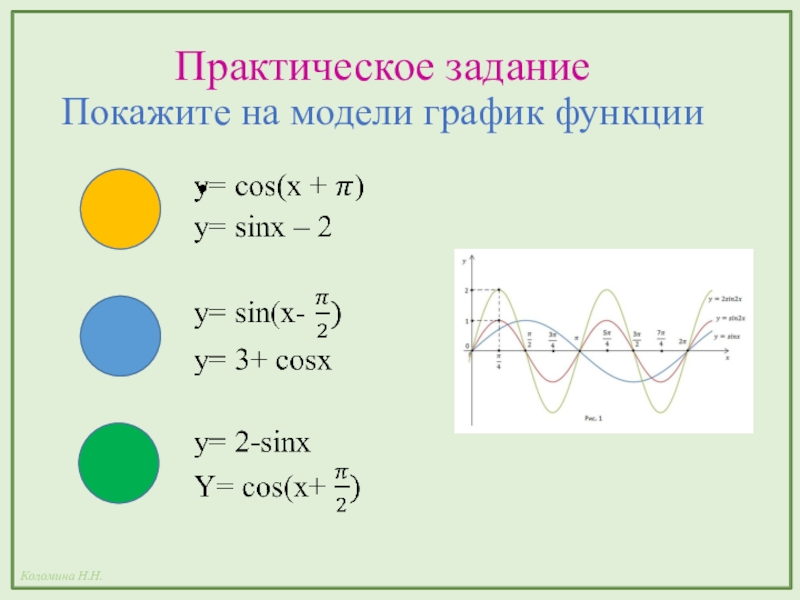
- 12. Практическое задание Покажите на модели график функции
- 13. Определите, сколько корней имеет уравнение
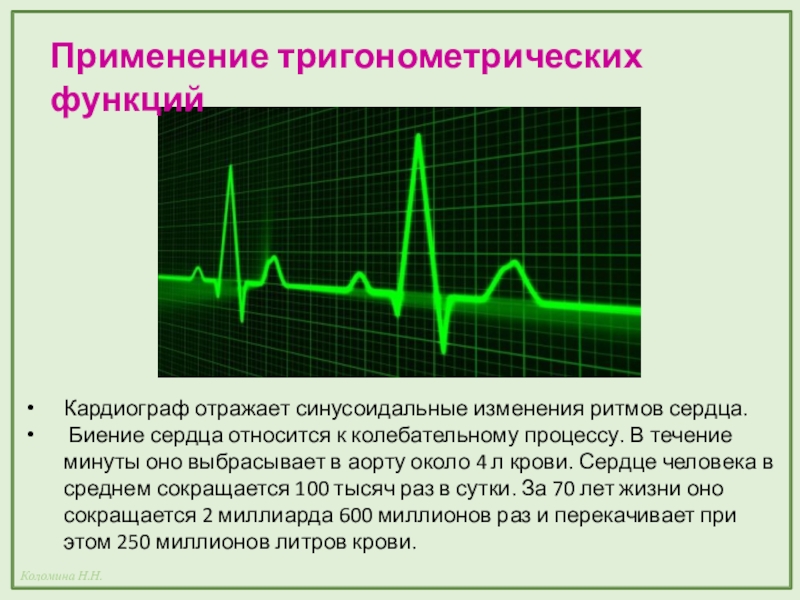
- 14. Кардиограф отражает синусоидальные изменения ритмов сердца. Биение
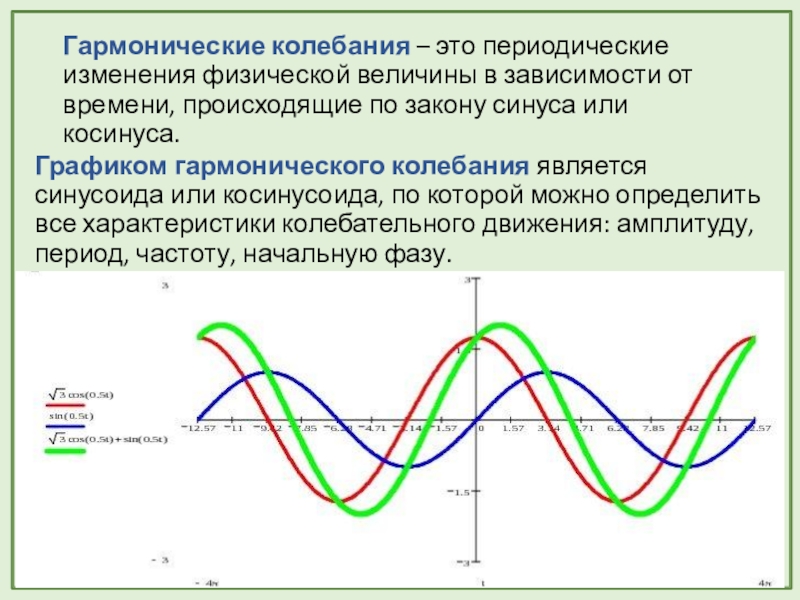
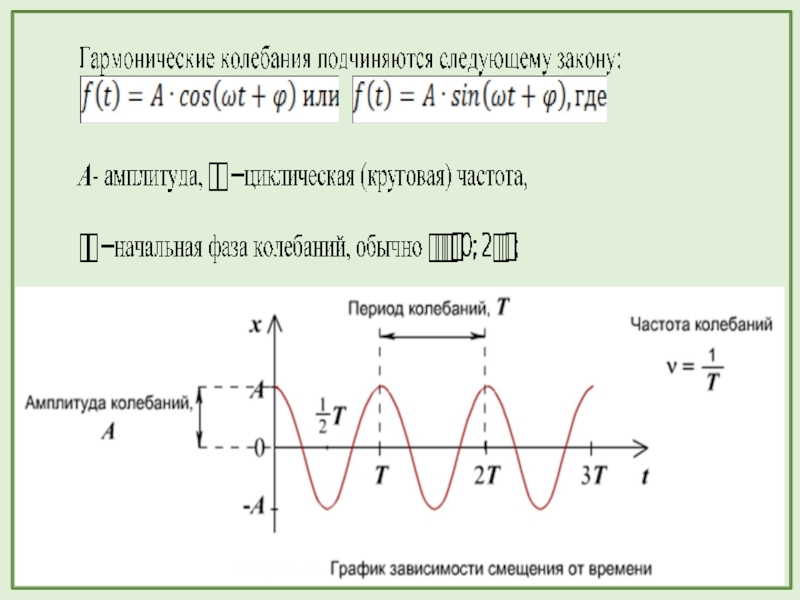
- 15. Гармонические колебания – это периодические изменения физической
- 16. Слайд 16
- 17. Слайд 17
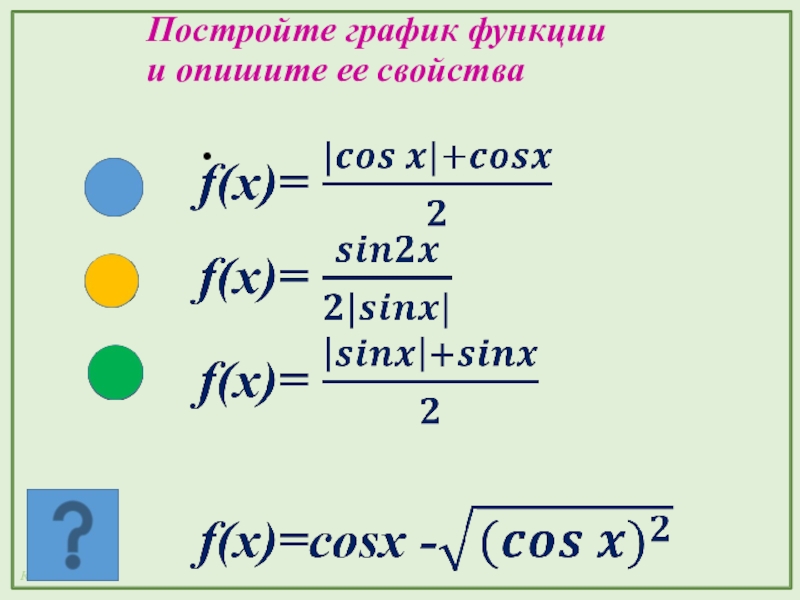
- 18. Постройте график функции и опишите ее свойства
- 19. Домашнее задание1) Построить график функции у =
- 20. Выберите одно из утверждений, которое вы считаете
[-3;5]0ху7-51Подумай!2[-5;7)3[-5;7]Подумай!4(-3;5]Подумай!Проверка Найдите область определения функции, график которой изображен на рисунке.5-3Верно!Область определения функции – значения, которые принимает независимая переменная х.
Слайд 2[-3;5]
0
х
у
7
-5
1
Подумай!
2
[-5;7)
3
[-5;7]
Подумай!
4
(-3;5]
Подумай!
Проверка
Найдите область определения функции, график которой изображен на рисунке.
5
-3
Верно!
Область
определения функции – значения, которые принимает независимая переменная х.
![[-3;5]0ху7-51Подумай!2[-5;7)3[-5;7]Подумай!4(-3;5]Подумай!Проверка Найдите область определения функции, график которой изображен на рисунке.5-3Верно!Область определения функции – значения, которые принимает](/img/thumbs/8638c7f66076cb7f577160ba72373b85-800x.jpg "Презентация по алгебре и началам анализа на тему Тригонометрические функции [-3;5]0ху7-51Подумай!2[-5;7)3[-5;7]Подумай!4(-3;5]Подумай!Проверка Найдите область определения функции, график которой изображен на рисунке.5-3Верно!Область определения")
Слайд 3 Найдите множество значений функции,
график которой изображен на рисунке.
у
х
0
-6
-4
6
6
1
2
3
4
Проверка
(-4;6)
[-6;6]
(-6;6)
[-4;6]
Подумай!
Верно!
Подумай!
Подумай!
Множество значений функции – значения, которые принимает зависимая переменная у.
Слайд 4 На одном из следующих рисунков изображен
график четной функции. Укажите этот график.
х
х
х
х
у
у
у
у
1
3
2
4
Подумай!
Верно!
Проверка
График симметричен относительно оси Oу
Подумай!
0
0
0
0
Подумай!
Слайд 51
2
3
4
х
х
х
х
у
у
у
у
На одном из следующих рисунков изображен
график нечетной функции. Укажите этот график.
Подумай!
Верно!
Подумай!
Проверка
График симметричен относительно точки О.
Подумай!
О
О
О
О
Слайд 61
2
3
4
[-6;7]
[-5;-3] U [2;6]
[-3;7]
[-3;2]
Проверка
х
0
2
6
-5
7
-3
-6
Подумай!
Подумай!
-2
3
Подумай !
На рисунке изображен график функции y =
f(x), заданной на промежутке (-5;6). Укажите промежутки, где функция возрастает.
у
Верно!
![1234[-6;7][-5;-3] U [2;6][-3;7][-3;2]Проверках026-57-3-6Подумай!Подумай!-23Подумай ! На рисунке изображен график функции y = f(x), заданной на](/img/tmb/5/465602/abc060bb719de3d0b0201bb20518f8fc-800x.jpg "Презентация по алгебре и началам анализа на тему Тригонометрические функции 1234[-6;7][-5;-3] U [2;6][-3;7][-3;2]Проверках026-57-3-6Подумай!Подумай!-23Подумай ! На рисунке изображен график функции y =")
Слайд 7y
х
1
2
3
4
1
2
4
0
Подумай!
Подумай!
Верно!
Подумай!
Проверка
Нуль функции – значение х, при котором y = 0. На
рисунке – это точки пересечения графика с осью Ох.
На рисунке изображен график функции y = f(x). Укажите количество нулей функции.
0
Слайд 11Работа в группах
Каждой группе определен свой цвет.
Необходимо выполнить задание соответствующего
цвета.
Слайд 14Кардиограф отражает синусоидальные изменения ритмов сердца.
Биение сердца относится к колебательному
процессу. В течение минуты оно выбрасывает в аорту около 4 л крови. Сердце человека в среднем сокращается 100 тысяч раз в сутки. За 70 лет жизни оно сокращается 2 миллиарда 600 миллионов раз и перекачивает при этом 250 миллионов литров крови.
Применение тригонометрических функций
Слайд 15Гармонические колебания – это периодические изменения физической величины в зависимости от
времени, происходящие по закону синуса или косинуса.
Графиком гармонического колебания является синусоида или косинусоида, по которой можно определить все характеристики колебательного движения: амплитуду, период, частоту, начальную фазу.
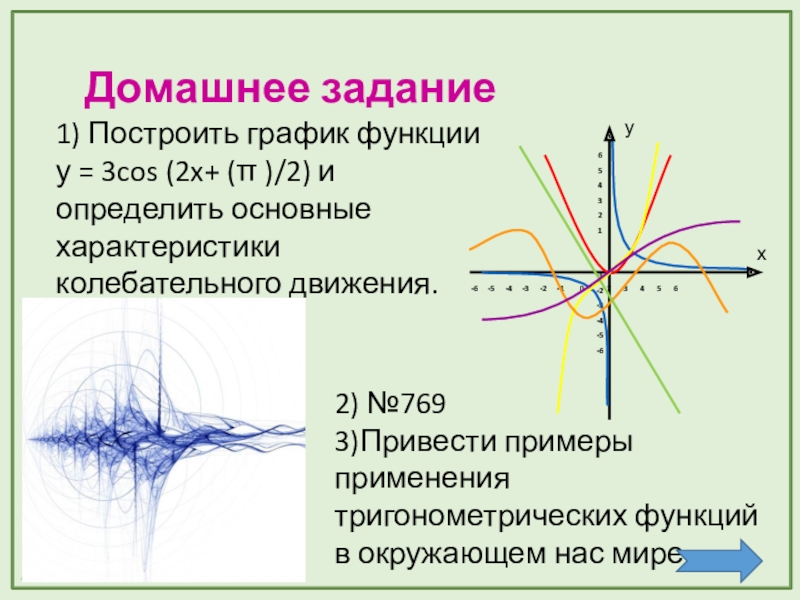
Слайд 19Домашнее задание
1) Построить график функции
у = 3cos (2x+ (π )/2)
и определить основные характеристики колебательного движения.
2) №769
3)Привести примеры применения тригонометрических функций в окружающем нас мире
Слайд 20Выберите одно из утверждений, которое вы считаете наиболее подходящим для вас.
• Я понял, как с помощью преобразований строить графики тригонометрических функций
• У меня есть вопросы по данной теме.
• Я понял, что нам нужно сделать, чтобы строить графики тригонометрических функций.
