- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад для учеников. Полезно и легко о вычислении площади многоугольника с собственными дырками
Содержание
- 1. Презентация для учеников. Полезно и легко о вычислении площади многоугольника с собственными дырками
- 2. Доказательство теоремы 1
- 3. Задача 2. Дырки, касающиеся сторон многоугольникаДан прямоугольник
- 4. Таблица вычисления пощади многоугольника с граничными дырками
- 5. Формула вычисления пощади многоугольника с граничными дырками
- 6. Доказательство теоремы 2
- 7. Формула вычисления пощади многоугольника с дырками двух видов
- 8. Пример. Вычислить площадь вырезанной из бумаги снежинки,
- 9. ЗаключениеВ работе рассмотрены два различных случая расположения
- 10. Спасибо за внимание!
Доказательство теоремы 1
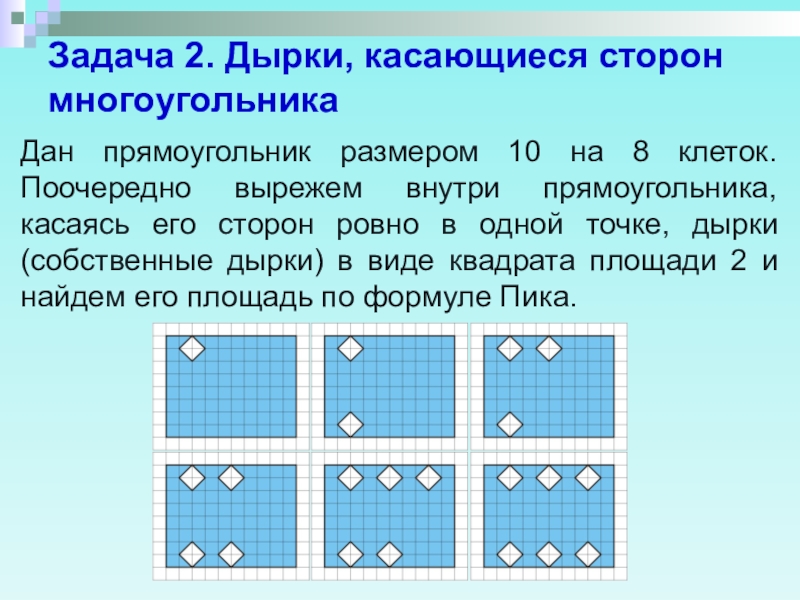
Слайд 3Задача 2. Дырки, касающиеся сторон многоугольника
Дан прямоугольник размером 10 на 8
клеток. Поочередно вырежем внутри прямоугольника, касаясь его сторон ровно в одной точке, дырки (собственные дырки) в виде квадрата площади 2 и найдем его площадь по формуле Пика.
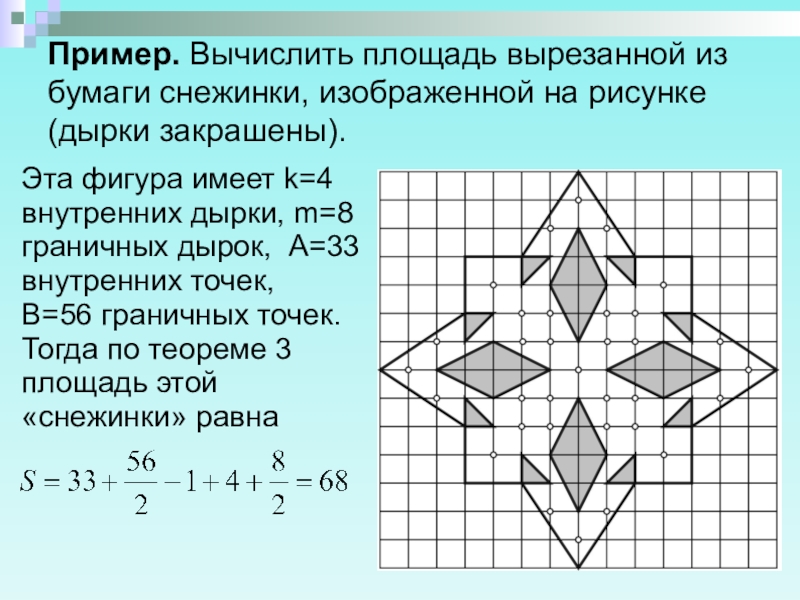
Слайд 8Пример. Вычислить площадь вырезанной из бумаги снежинки, изображенной на рисунке (дырки
закрашены).
Эта фигура имеет k=4 внутренних дырки, m=8 граничных дырок, А=33 внутренних точек, В=56 граничных точек. Тогда по теореме 3 площадь этой «снежинки» равна
Слайд 9Заключение
В работе рассмотрены два различных случая расположения дырок внутри многоугольника: без
касания сторон многоугольника и с касанием сторон многоугольника в одной точке.
Основные результаты работы :
1) мы установили, что существует зависимость между расположением дырок внутри многоугольника и изменением формулы Пика для вычисления площади такого многоугольника;
2) получили изменённые формулы Пика для вычисления площади многоугольника с тремя видами дырок.
Основные результаты работы :
1) мы установили, что существует зависимость между расположением дырок внутри многоугольника и изменением формулы Пика для вычисления площади такого многоугольника;
2) получили изменённые формулы Пика для вычисления площади многоугольника с тремя видами дырок.