Презентация, доклад для проведения математической регаты в 9 классе

6 баллов).
1.1. Решите уравнение: x(x + 1) = 2014*2015.
1.2. Три пирата нашли клад, состоящий из 240 золотых слитков общей стоимостью 360 долларов. Стоимость каждого слитка известна и выражается целым числом долларов. Может ли оказаться так, что добычу нельзя разделить между пиратами поровну, не переплавляя слитки?

x(x + 1) = 20142015.
Ответ: 2014; 2015.

Решение. Так как каждая часть уравнения представляет собой произведение двух последовательных чисел, то оба корня подбираются исходя из предположения, что они целые, а их модули могут быть равны 2014 или 2015. Данное уравнение – квадратное, поэтому имеет не более двух корней.
Если один корень уже подобран, то второй может быть найден по теореме Виета.
1.2. Ответ: да, может.

Решение. Пусть один из слитков стоит 121 доллар, а каждый из остальных слитков стоит 1 доллар (таких слитков будет 239). Так как каждому пирату должно достаться слитков ровно на 120 долларов, то в этом случае разделить добычу поровну будет невозможно.

идет по дороге со скоростью 4 км/ч. Увидев пенек, она садится на него и отдыхает одно и то же целое число минут. Михаил Потапович идет по той же дороге со скоростью 5 км/ч, зато сидит на каждом пеньке в два раза дольше, чем Марья Петровна. Вышли и пришли они одновременно. Длина дороги – 11 км. Сколько на ней могло быть пеньков?
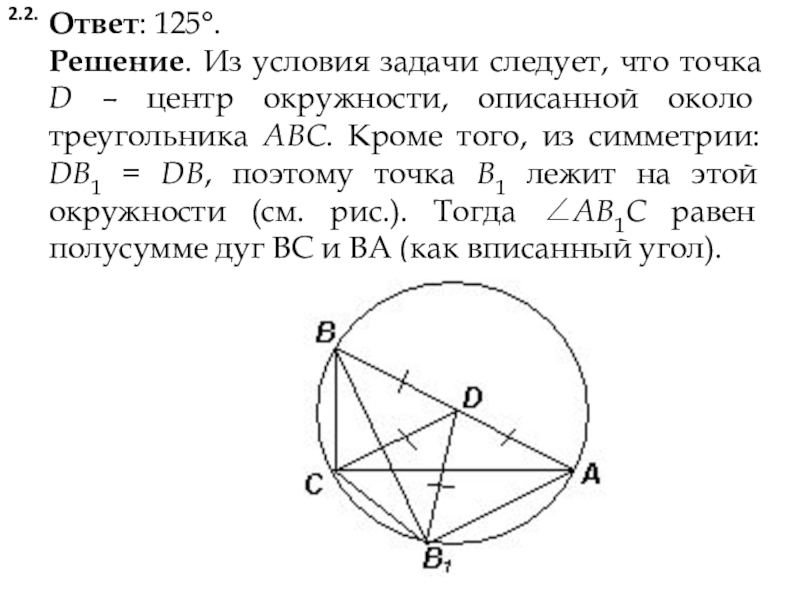
2.2. Точка D — середина гипотенузы АВ прямоугольного треугольника ABC, угол ВАС равен 35°. Точка B1 симметрична точке B относительно прямой СD. Найдите угол AB1C.

3, 11 или 33 пенька.
Решение. Марья Петровна преодолевает указанную дистанцию за 11/4 часа, а Михаил Потапович – за 11/5 часа. Следовательно, Марья Петровна отдыхает на 11/4-11/5=11/20 ч больше, что составляет 33 минуты.
Так как на каждом пеньке Марья Петровна сидит целое число минут и количество пеньков – целое, то на каждом пеньке она могла сидеть 33, 11, 3 или 1 минуту, что соответствует 1, 3, 11 или 33 пенькам.

центр окружности, описанной около треугольника ABC. Кроме того, из симметрии: DB1 = DB, поэтому точка B1 лежит на этой окружности (см. рис.). Тогда AB1C равен полусумме дуг ВС и ВА (как вписанный угол).

Какие значения может принимать выражение

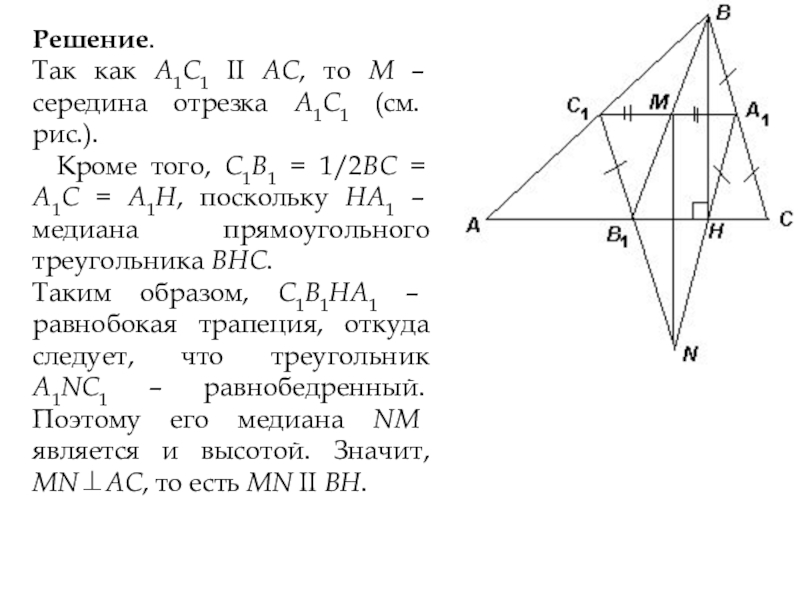
3.2. В треугольнике АВС проведены высота ВН, медиана ВВ1
и средняя линия А1С1 (А1 лежит на стороне ВС, С1 – на стороне АВ).
Прямые А1С1 и ВВ1 пересекаются в точке М, а прямые С1В1 и А1Н – в точке N. Докажите, что прямые MN и BH параллельны.

8.
Решение. Перепишем условие в виде:

тогда , , .
Сложим полученные равенства почленно:

,

Возможны два случая:

,

тогда = –1;

или ,

тогда = 8.


Можно также провести аналогичное рассуждение, не «переворачивая» дроби, заданные в условии.

А1С1 (см. рис.).
Кроме того, С1В1 = 1/2ВС = А1С = А1Н, поскольку НА1 – медиана прямоугольного треугольника ВНС.
Таким образом, С1В1НА1 – равнобокая трапеция, откуда следует, что треугольник А1NС1 – равнобедренный. Поэтому его медиана NM является и высотой. Значит, MNАС, то есть MN II BH.