- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад для подготовки к экзамену по профильной математике Решение вероятностных задач
Содержание
- 1. Презентация для подготовки к экзамену по профильной математике Решение вероятностных задач
- 2. 1. Если шахматист А. играет белыми фигурами,
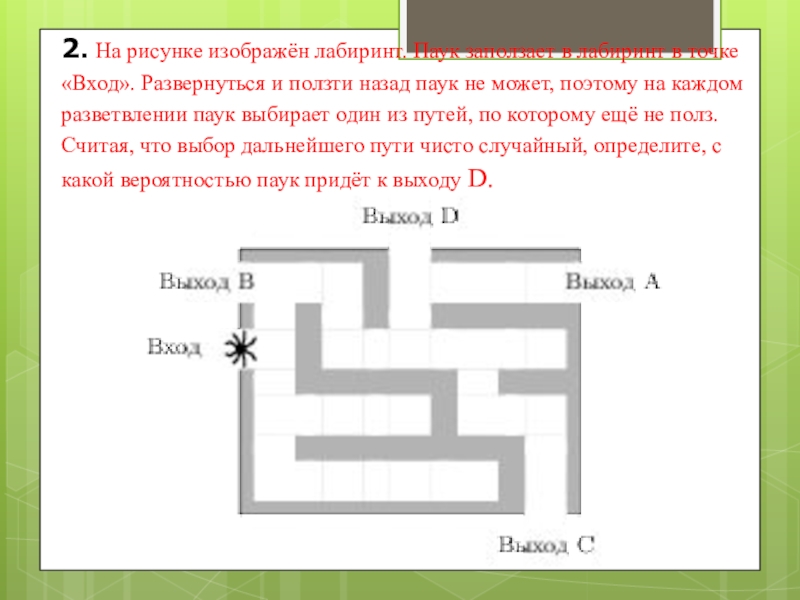
- 3. 2. На рисунке изображён лабиринт. Паук заползает
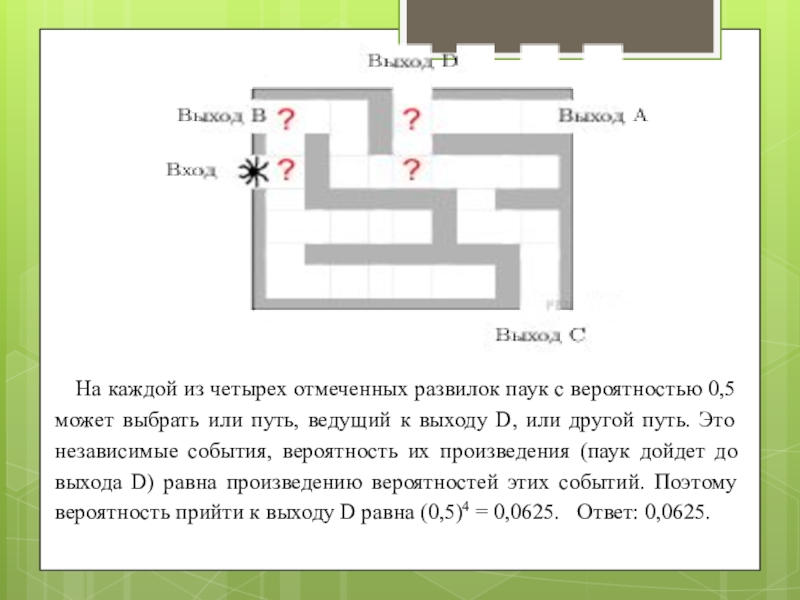
- 4. На каждой из четырех отмеченных развилок паук
- 5. 3. Вероятность того, что батарейка бракованная, равна
- 6. 4. Какова вероятность того, что случайно выбранный
- 7. События A, В и С несовместные, вероятность их суммы равна сумме вероятностей этих событий.
- 8. 5. Вероятность того, что новый электрический чайник
- 9. 6. Из районного центра в деревню ежедневно
- 10. 7. В магазине три продавца. Каждый из
- 11. 8. В торговом центре два одинаковых автомата
- 12. Решение.Рассмотрим событияА = кофе закончится в первом
- 13. 9. Вероятность того, что в случайный момент
- 14. 10. При изготовлении подшипников диаметром 67 мм
- 15. 11. Биатлонист пять раз стреляет по мишеням.
- 16. 12. Помещение освещается фонарём с двумя лампами.
- 17. 13. При артиллерийской стрельбе автоматическая система делает
- 18. 14. На экзамене по геометрии школьник отвечает
- 19. 15 Чтобы пройти в следующий круг соревнований,
- 20. 16. В Волшебной стране бывает два типа
Слайд 21. Если шахматист А. играет белыми фигурами, то он выигрывает у
Решение.
Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: 0,5 · 0,3 = 0,15. Ответ: 0,15.
Вероятность того, что происходит несколько независимых событий, равна произведению вероятностей.
Слайд 32. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке
Слайд 4На каждой из четырех отмеченных развилок паук с вероятностью 0,5 может
Слайд 53. Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине
Решение.
Вероятность того, что батарейка исправна, равна
1 – 0,06 = 0,94.
Вероятность произведения независимых событий (обе батарейки окажутся исправными) равна произведению вероятностей этих событий:
0,94·0,94 = 0,8836.
Ответ: 0,8836.
Слайд 64. Какова вероятность того, что случайно выбранный телефонный номер оканчивается двумя
Решение.
Вероятность того, что на одном из требуемых мест окажется чётное число равна 0,5. Следовательно, вероятность того, что на двух местах одновременно окажутся два чётных числа равна 0,5 · 0,5=0,25. Ответ: 0,25.
Слайд 85. Вероятность того, что новый электрический чайник прослужит больше года, равна
Решение.
Пусть A = «чайник прослужит больше года, но меньше двух лет», В = «чайник прослужит больше двух лет», С = «чайник прослужит ровно два года», тогда A + B + С = «чайник прослужит больше года».
Вероятность события С, состоящего в том, что чайник выйдет из строя ровно через два года — строго в тот же день, час и секунду — равна нулю. Тогда:
P(A + B+ С) = P(A) + P(B)+ P(С)= P(A) + P(B),
откуда, используя данные из условия, получаем
0,93 = P(A) + 0,87.
Тем самым, для искомой вероятности имеем:
P(A) = 0,93 − 0,87 = 0,06. Ответ: 0,06.
Слайд 96. Из районного центра в деревню ежедневно ходит автобус. Вероятность того,
Решение.
Рассмотрим события A = «в автобусе меньше 10 пассажиров» и В = «в автобусе от 10 до 17 пассажиров». Их сумма — событие A + B = «в автобусе меньше 18 пассажиров». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий: P(A + B) = P(A) + P(B).
Тогда, используя данные задачи, получаем: 0,82 = 0,51 + P(В), откуда
P(В) = 0,82 − 0,51 = 0,31. Ответ: 0,31.
Слайд 107. В магазине три продавца. Каждый из них занят с клиентом
Решение.
Вероятность произведения независимых событий равна произведению вероятностей этих событий. Поэтому вероятность того, что все три продавца заняты равна 0,33.Ответ: 0,027.
Слайд 118. В торговом центре два одинаковых автомата продают кофе. Обслуживание автоматов
Слайд 12Решение.
Рассмотрим события
А = кофе закончится в первом автомате,
В = кофе закончится
Тогда
A·B = кофе закончится в обоих автоматах,
A + B = кофе закончится хотя бы в одном автомате.
По условию P(A) = P(B) = 0,25; P(A·B) = 0,15.
События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:
P(A + B) = P(A) + P(B) − P(A·B) = 0,25 + 0,25 − 0,15 = 0,35.
Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,35 = 0,65. Ответ: 0,65.
Слайд 139. Вероятность того, что в случайный момент времени температура тела здорового
Решение.
Указанные события противоположны, поэтому искомая вероятность равна 1 − 0,81 = 0,19. Ответ: 0,19.
Слайд 1410. При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр
Решение. По условию, диаметр подшипника будет лежать в пределах от 66,99 до 67,01 мм с вероятностью 0,965. Поэтому искомая вероятность противоположного события равна 1 − 0,965 = 0,035. Ответ: 0,035.
Слайд 1511. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень
Решение.
Поскольку биатлонист попадает в мишени с вероятностью 0,8, он промахивается с вероятностью 1 − 0,8 = 0,2. Cобытия попасть или промахнуться при каждом выстреле независимы, вероятность произведения независимых событий равна произведению их вероятностей. Тем самым, вероятность события «попал, попал, попал, промахнулся, промахнулся» равна
0,8∙0,8∙0,8∙0,2∙0,2 = 0,02048 ≈ 0,02. Ответ: 0,02.
Слайд 1612. Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы в
Решение.
Найдем вероятность того, что перегорят обе лампы. Эти события независимые, вероятность их произведения равно произведению вероятностей этих событий: 0,3·0,3 = 0,09.
Событие, состоящее в том, что не перегорит хотя бы одна лампа, противоположное. Следовательно, его вероятность равна 1 − 0,09 = 0,91. Ответ: 0,91.
Слайд 1713. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если
Решение.
Можно решать задачу «по действиям», вычисляя вероятность уцелеть после ряда последовательных промахов:
Р(1) = 0,6. Р(2) = Р(1)·0,4 = 0,24. Р(3) = Р(2)·0,4 = 0,096.
Р(4) = Р(3)·0,4 = 0,0384; Р(5) = Р(4)·0,4 = 0,01536.
Последняя вероятность меньше 0,02, поэтому достаточно пяти выстрелов по мишени. Ответ: 5.
Слайд 1814. На экзамене по геометрии школьник отвечает на один вопрос из
Решение.
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: 0,2 + 0,15 = 0,35. Ответ: 0,35.
Слайд 1915 Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать
Решение.
Команда может получить не меньше 4 очков в двух играх тремя способами: 3+1, 1+3, 3+3. Эти события несовместны, вероятность их суммы равна сумме их вероятностей. Каждое из этих событий представляет собой произведение двух независимых событий — результата в первой и во второй игре. Отсюда имеем:
Вероятность ничьей равна 1 − 0,4 − 0,4 = 0,2.
Ответ: 0,32.
Слайд 2016. В Волшебной стране бывает два типа погоды: хорошая и отличная,
Решение.
Для погоды на 4, 5 и 6 июля есть 4 варианта: ХХО, ХОО, ОХО, ООО (здесь Х — хорошая, О — отличная погода). Найдем вероятности наступления такой погоды:
P(XXO) = 0,8·0,8·0,2 = 0,128; P(XOO) = 0,8·0,2·0,8 = 0,128;
P(OXO) = 0,2·0,2·0,2 = 0,008 P(OOO) = 0,2·0,8·0,8 = 0,128.
Указанные события несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) = 0,128 + 0,128 + 0,008 + 0,128 = 0,392. Ответ: 0,392.