- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад для подготовки к ЕГЭ, ОГЭ
Содержание
- 1. Презентация для подготовки к ЕГЭ, ОГЭ
- 2. «Трудное сделать легким, легкое привычным, привычное приятным!»
- 3. Слайд 3
- 4. Свойства вероятностиВероятность случайного события есть положительное число,
- 5. В фирме такси в наличии 50 легковых
- 6. Решение: Машин желтого цвета с черными надписями
- 7. На олимпиаде в вузе участников рассаживают по
- 8. Решение: Всего в запасную аудиторию направили 250 − 120
- 9. В группе туристов 5 человек. С помощью
- 10. Решение: Всего туристов пять, случайным образом из
- 11. Вася, Петя, Коля и Лёша бросили жребий –
- 12. Решение: Вероятность того, что игру должен будет
- 13. На семинар приехали 3 ученых из Норвегии,
- 14. Решение: Всего участвует 3 + 3 +
- 15. Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три?
- 16. Решение: 10, 11, 12, 13, 14, 15,
- 17. Слайд 17
- 18. Пусть k – количество бросков монеты, тогда количество всевозможных исходов: n = 2k.
- 19. Задачи на подбрасывание кубика
- 20. Пусть k – количество бросков кубика, тогда количество всевозможных исходов: n = 6k.
- 21. Монету подбрасывают 2 раза (подбрасывают 2 монеты)Бросаются
- 22. В случайном эксперименте бросают две игральные кости.
- 23. Решение.Подсчитаем количество исходов (вариантов), в которых сумма
- 24. Даша дважды бросает игральный кубик. В сумме
- 25. В сумме на двух кубиках должно выпасть
- 26. Тоша и Гоша играют в кости. Они
- 27. Решение.При условии, что у Тоши выпало 3
- 28. Перед началом футбольного матча судья бросает монету,
- 29. Решение: Обозначим право владения первой мячом команды
- 30. Исходы в связке И ⇒ Итожь ⇒ Вероятности умножь. Исходы в связке ИЛИ ⇒ Вероятности сложИЛИ.
- 31. На экзамене по геометрии школьнику достаётся один
- 32. Решение: Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:р = 0,2 + 0,15 = 0,35. Ответ: 0,35
- 33. Биатлонист пять раз стреляет по мишеням. Вероятность
- 34. Решение: Результат каждого следующего выстрела не зависит
- 35. Помещение освещается фонарём с двумя лампами. Вероятность
- 36. Решение: Найдем вероятность того, что перегорят обе
- 37. В магазине три продавца. Каждый из них
- 38. Решение: Вероятность произведения независимых событий равна произведению
- 39. Ковбой Джон попадает в муху на стене
- 40. Вероятность того, что Джон промахнется, если схватит
- 41. По отзывам покупателей Иван Иванович оценил надёжность
- 42. Вероятность того, что первый магазин не доставит
- 43. На рисунке изображён лабиринт. Паук заползает в
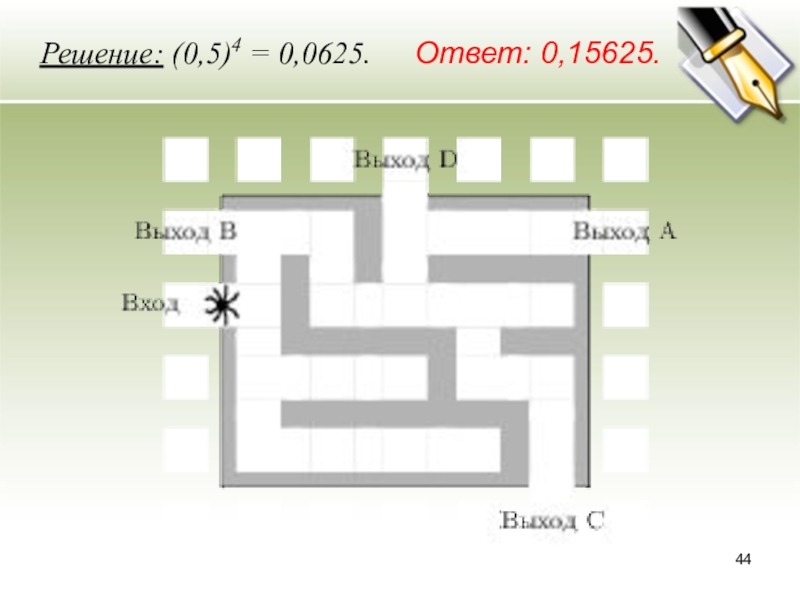
- 44. Решение: (0,5)4 = 0,0625. Ответ: 0,15625.
- 45. Автоматическая линия изготавливает батарейки. Вероятность того, что
- 46. Решение: Ситуация, при которой батарейка будет забракована,
- 47. Всем пациентам с подозрением на гепатит делают
- 48. Решение: Анализ пациента может быть положительным по
- 49. Агрофирма закупает куриные яйца в двух домашних
- 50. Решение: Пусть х – искомая вероятность того,
- 51. В Волшебной стране бывает два типа погоды:
- 52. Для погоды на 4, 5 и 6
- 53. Слайд 53
«Трудное сделать легким, легкое привычным, привычное приятным!»
Слайд 4Свойства вероятности
Вероятность случайного события есть положительное число, заключенное между нулем и
единицей: 0 ≤ Р(А) ≤ 1.
Слайд 5В фирме такси в наличии 50 легковых автомобилей; 27 из них
чёрные с жёлтыми надписями на бортах, остальные – жёлтые с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.
Слайд 6Решение:
Машин желтого цвета с черными надписями 23, всего машин 50.
Поэтому вероятность того, что на случайный вызов приедет машина желтого цвета с черными надписями, равна:
P = 23 : 50 = 0,46. Ответ: 0,46.
P = 23 : 50 = 0,46. Ответ: 0,46.
Слайд 7На олимпиаде в вузе участников рассаживают по трём аудиториям. В первых
двух по 120 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было 250 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
Слайд 8Решение:
Всего в запасную аудиторию направили
250 − 120 − 120 = 10 человек.
Поэтому вероятность
того, что случайно выбранный участник писал олимпиаду в запасной аудитории, равна
P = 10 : 250 = 0,04. Ответ: 0,04.
P = 10 : 250 = 0,04. Ответ: 0,04.
Слайд 9В группе туристов 5 человек. С помощью жребия они выбирают двух
человек, которые должны идти в село за продуктами. Турист А. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что А. пойдёт в магазин?
Слайд 10Решение:
Всего туристов пять, случайным образом из них выбирают двоих.
Вероятность
быть выбранным равна
Р = 2/5 = 0,4.
Ответ: 0,4.
Р = 2/5 = 0,4.
Ответ: 0,4.
Слайд 11Вася, Петя, Коля и Лёша бросили жребий – кому начинать игру. Найдите
вероятность того, что начинать игру должен будет Петя.
Слайд 12Решение:
Вероятность того, что игру должен будет начинать любой из мальчиков
равна 1/4 = 0,25.
В том числе и для Пети.
Ответ: 0,25.
В том числе и для Пети.
Ответ: 0,25.
Слайд 13На семинар приехали 3 ученых из Норвегии, 3 из России и
4 из Испании. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России.
Слайд 14Решение:
Всего участвует 3 + 3 + 4 = 10 ученых.
Вероятность того, что восьмым окажется доклад ученого из России, равна 3/10 = 0,3.
Ответ: 0,3
Слайд 15Какова вероятность того, что случайно выбранное натуральное число от 10 до
19 делится на три?
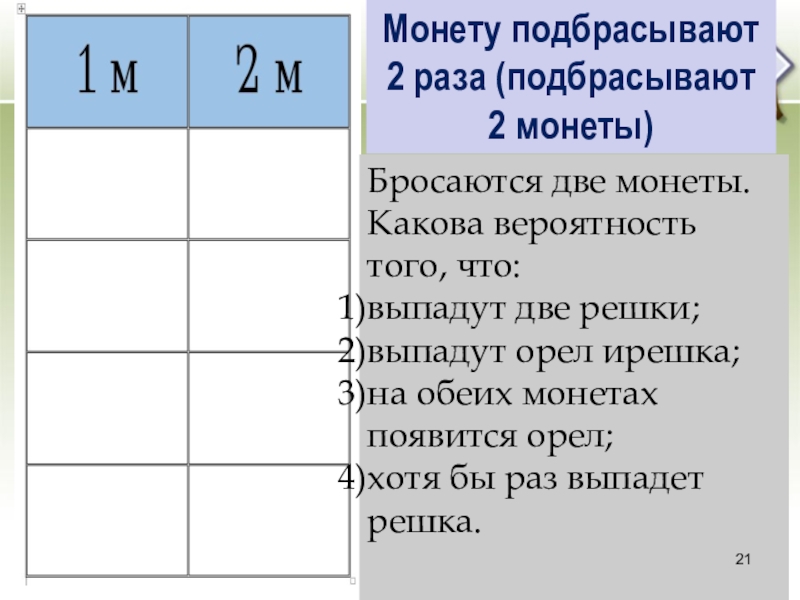
Слайд 21Монету подбрасывают 2 раза (подбрасывают 2 монеты)
Бросаются две монеты. Какова вероятность
того, что:
выпадут две решки;
выпадут орел ирешка;
на обеих монетах появится орел;
хотя бы раз выпадет решка.
выпадут две решки;
выпадут орел ирешка;
на обеих монетах появится орел;
хотя бы раз выпадет решка.
Слайд 22В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что
в сумме выпадет 8 очков. Результат округлите до сотых.
Слайд 23Решение.
Подсчитаем количество исходов (вариантов), в которых сумма очков двух кубиков равна
8.
2; 6 3; 5; 4; 4 5; 3 6; 2.
Всего 5 вариантов.
Найдем вероятность: 5/36 = 0,138 ≈ 0,14.
Ответ: 0,14.
2; 6 3; 5; 4; 4 5; 3 6; 2.
Всего 5 вариантов.
Найдем вероятность: 5/36 = 0,138 ≈ 0,14.
Ответ: 0,14.
Слайд 24Даша дважды бросает игральный кубик. В сумме у нее выпало 8
очков. Найдите вероятность того, что при первом броске выпало 2 очка.
Слайд 25В сумме на двух кубиках должно выпасть 8 очков. Это возможно,
если будут следующие комбинации:
2 и 6
6 и 2
3 и 5
5 и 3
4 и 4
Всего 5 вариантов. Подсчитаем количество исходов (вариантов), в которых при первом броске выпало 2 очка.
Такой вариант 1.
Найдем вероятность: 1/5 = 0,2.
Ответ: 0,2.
2 и 6
6 и 2
3 и 5
5 и 3
4 и 4
Всего 5 вариантов. Подсчитаем количество исходов (вариантов), в которых при первом броске выпало 2 очка.
Такой вариант 1.
Найдем вероятность: 1/5 = 0,2.
Ответ: 0,2.
Слайд 26Тоша и Гоша играют в кости. Они бросают кубик по одному
разу. Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. Первым бросил Тоша, у него выпало 3 очка. Найдите вероятность того, что Гоша не выиграет.
Слайд 27Решение.При условии, что у Тоши выпало 3 очка, возможны следующие варианты:
3
и 1
3 и 2
3 и 3
3 и 4
3 и 5
3 и 6
Всего 6 вариантов. Подсчитаем количество исходов, в которых Гоша не выиграет, т.е. наберет 1, 2 или 3 очка.
Таких вариантов 3.
Найдем вероятность: 3/6 = 0,5. Ответ: 0,5
3 и 2
3 и 3
3 и 4
3 и 5
3 и 6
Всего 6 вариантов. Подсчитаем количество исходов, в которых Гоша не выиграет, т.е. наберет 1, 2 или 3 очка.
Таких вариантов 3.
Найдем вероятность: 3/6 = 0,5. Ответ: 0,5
Слайд 28Перед началом футбольного матча судья бросает монету, чтобы определить, какая из
команд будет первая владеть мячом. Команда "Меркурий" по очереди играет с командами "Марс", "Юпитер", "Уран". Найдите вероятность того, что во всех матчах право владеть мячом выиграет команда "Меркурий"?
Слайд 29Решение: Обозначим право владения первой мячом команды "Меркурий" в матче с
одной из других трех команд как "Решка". Тогда право владения второй мячом этой команды – «Орел». Итак, напишем все возможные исходы бросания монеты три раза.
«О» – орел, «Р» – решка.
Итак, всего исходов получилось 8, нужных нам – 1, следовательно,
вероятность выпадения нужного исхода 1/8 = 0,125.
Ответ: 0,125.
«О» – орел, «Р» – решка.
Итак, всего исходов получилось 8, нужных нам – 1, следовательно,
вероятность выпадения нужного исхода 1/8 = 0,125.
Ответ: 0,125.
Слайд 31На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных
вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Слайд 32Решение:
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
р
= 0,2 + 0,15 = 0,35.
Ответ: 0,35
Ответ: 0,35
Слайд 33Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при
одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два раза промахнулся. Результат округлите до сотых.
Слайд 34Решение:
Результат каждого следующего выстрела не зависит от предыдущих. Поэтому события
«попал при первом выстреле», «попал при втором выстреле» и т.д. независимы.Вероятность каждого попадания равна 0,8. Значит, вероятность промаха равна 1 – 0,8 = 0,2.
1 выстрел: 0,8
2 выстрел: 0,8
3 выстрел: 0,8
4 выстрел: 0,2
5 выстрел: 0,2
По формуле умножения вероятностей независимых событий, получаем, что искомая вероятность равна:
0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2 = 0,02048 ≈ 0,02. Ответ: 0,02.
1 выстрел: 0,8
2 выстрел: 0,8
3 выстрел: 0,8
4 выстрел: 0,2
5 выстрел: 0,2
По формуле умножения вероятностей независимых событий, получаем, что искомая вероятность равна:
0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2 = 0,02048 ≈ 0,02. Ответ: 0,02.
Слайд 35Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в
течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Слайд 36Решение:
Найдем вероятность того, что перегорят обе лампы.
Эти события независимые,
вероятность их произведения равна произведению вероятностей этих событий: р1 = 0,3 · 0,3 = 0,09.
Событие, состоящее в том, что не перегорит хотя бы одна лампа, противоположное.
Следовательно, его вероятность равна
р = 1 – р1 = 1 − 0,09 = 0,9
Ответ: 0,91.
1.
Событие, состоящее в том, что не перегорит хотя бы одна лампа, противоположное.
Следовательно, его вероятность равна
р = 1 – р1 = 1 − 0,09 = 0,9
Ответ: 0,91.
1.
Слайд 37В магазине три продавца. Каждый из них занят с клиентом с
вероятностью 0,3. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга).
Слайд 38Решение:
Вероятность произведения независимых событий равна произведению вероятностей этих событий.
Поэтому
вероятность того, что все три продавца заняты равна:
р= 0,3*0,3*0,3=0,027
Ответ: 0,027.
р= 0,3*0,3*0,3=0,027
Ответ: 0,027.
Слайд 39Ковбой Джон попадает в муху на стене с вероятностью 0,9, если
стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Слайд 40Вероятность того, что Джон промахнется, если схватит пристрелянный револьвер равна:
0,4 ·
(1 − 0,9) = 0,04
Вероятность того, что Джон промахнется, если схватит непристрелянный револьвер равна:
0,6 · (1 − 0,2) = 0,48
Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий:
0,04 + 0,48 = 0,52.
Ответ: 0,52
Вероятность того, что Джон промахнется, если схватит непристрелянный револьвер равна:
0,6 · (1 − 0,2) = 0,48
Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий:
0,04 + 0,48 = 0,52.
Ответ: 0,52
Слайд 41По отзывам покупателей Иван Иванович оценил надёжность двух интернет-магазинов. Вероятность того,
что нужный товар доставят из магазина А, равна 0,8. Вероятность того, что этот товар доставят из магазина Б, равна 0,9. Иван Иванович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
Слайд 42Вероятность того, что первый магазин не доставит товар равна:
Р1 = 1 − 0,9 = 0,1.
Вероятность того, что второй магазин не доставит товар равна:
Р2 = 1 − 0,8 = 0,2.
Поскольку эти события независимы, вероятность их произведения (оба магазина не доставят товар) равна произведению вероятностей этих событий:
Р1 · Р2 = 0,1 · 0,2 = 0,02.
Ответ: 0,02.
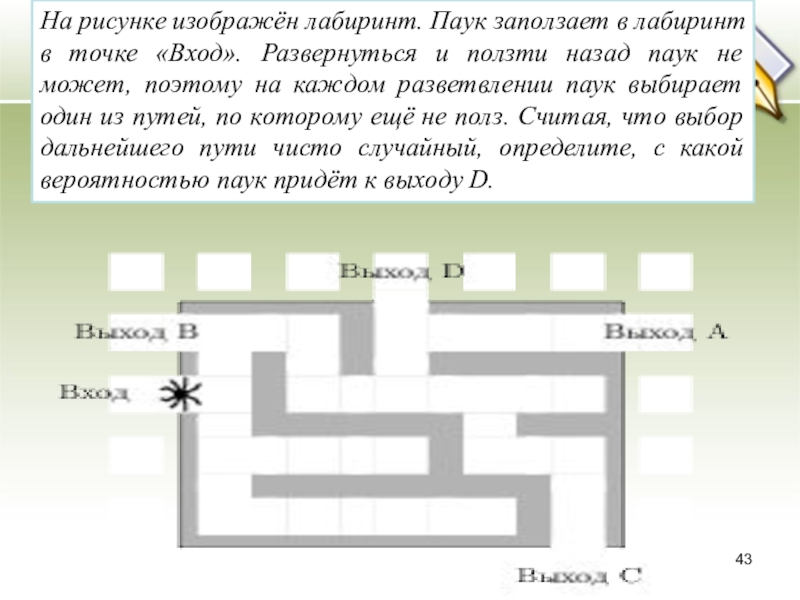
Слайд 43На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход».
Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу D.
Слайд 45Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна
0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Слайд 46Решение:
Ситуация, при которой батарейка будет забракована, может сложиться в результате
событий:
A = «батарейка действительно неисправна и забракована» или
В = «батарейка исправна, но по ошибке забракована».
Это несовместные события, вероятность их суммы равна сумме вероятностей эти событий.
Имеем:
P(A + B) = P(A) + P(B) = 0,02 · 0,99 + 0,98 · 0,01 =
= 0,0198 + 0,0098 = 0,0296.
A = «батарейка действительно неисправна и забракована» или
В = «батарейка исправна, но по ошибке забракована».
Это несовместные события, вероятность их суммы равна сумме вероятностей эти событий.
Имеем:
P(A + B) = P(A) + P(B) = 0,02 · 0,99 + 0,98 · 0,01 =
= 0,0198 + 0,0098 = 0,0296.
Слайд 47Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ
выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Слайд 48Решение:
Анализ пациента может быть положительным по двум причинам: а) пациент
болеет гепатитом, его анализ верен;
б) пациент не болеет гепатитом, его анализ ложен.
Это несовместные события, вероятность их суммы равна сумме вероятностей этих событий. Имеем:
P(A) = 0,9 · 0,05 = 0,045,
P(B) = 0,01 · 0,95 = 0,0095,
P(A + B) = P(A) + P(B) = 0,045 + 0,0095 = 0,0545. Ответ: 0,0545.
б) пациент не болеет гепатитом, его анализ ложен.
Это несовместные события, вероятность их суммы равна сумме вероятностей этих событий. Имеем:
P(A) = 0,9 · 0,05 = 0,045,
P(B) = 0,01 · 0,95 = 0,0095,
P(A + B) = P(A) + P(B) = 0,045 + 0,0095 = 0,0545. Ответ: 0,0545.
Слайд 49Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из
первого хозяйства – яйца высшей категории, а из второго хозяйства – 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Слайд 50Решение: Пусть х – искомая вероятность того, что куплено яйцо, произведенное
в первом хозяйстве.
Тогда 1 – х вероятность того, что куплено яйцо, произведенное во втором хозяйстве.
По формуле полной вероятности имеем:
0,4х + 0,2(1 – х) = 0,35
0,2х = 0,15
х = 0,75 Ответ: 0,75.
Тогда 1 – х вероятность того, что куплено яйцо, произведенное во втором хозяйстве.
По формуле полной вероятности имеем:
0,4х + 0,2(1 – х) = 0,35
0,2х = 0,15
х = 0,75 Ответ: 0,75.
Слайд 51В Волшебной стране бывает два типа погоды: хорошая и отличная, причём
погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
.
.
Слайд 52Для погоды на 4, 5 и 6 июля есть 4 варианта:
ХХО, ХОО, ОХО, ООО (здесь Х — хорошая, О — отличная погода). Найдем вероятности наступления такой погоды:
P(XXO) = 0,8·0,8·0,2 = 0,128;
P(XOO) = 0,8·0,2·0,8 = 0,128;
P(OXO) = 0,2·0,2·0,2 = 0,008;
P(OOO) = 0,2·0,8·0,8 = 0,128.
Указанные события несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) =
= 0,128 + 0,128 + 0,008 + 0,128 = 0,392.
P(XXO) = 0,8·0,8·0,2 = 0,128;
P(XOO) = 0,8·0,2·0,8 = 0,128;
P(OXO) = 0,2·0,2·0,2 = 0,008;
P(OOO) = 0,2·0,8·0,8 = 0,128.
Указанные события несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) =
= 0,128 + 0,128 + 0,008 + 0,128 = 0,392.