Учителя Новопокровской ош
Глухова Виктора Владимировича
Новопокровка 2014 – 2015 уч. год
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад – пособие Преобразование графиков функций
Содержание
- 1. Презентация – пособие Преобразование графиков функций
- 2. Рассмотрим преобразования графика функции у
- 3. Прямая пропорциональность y = k x
- 4. График линейной функции y = k x
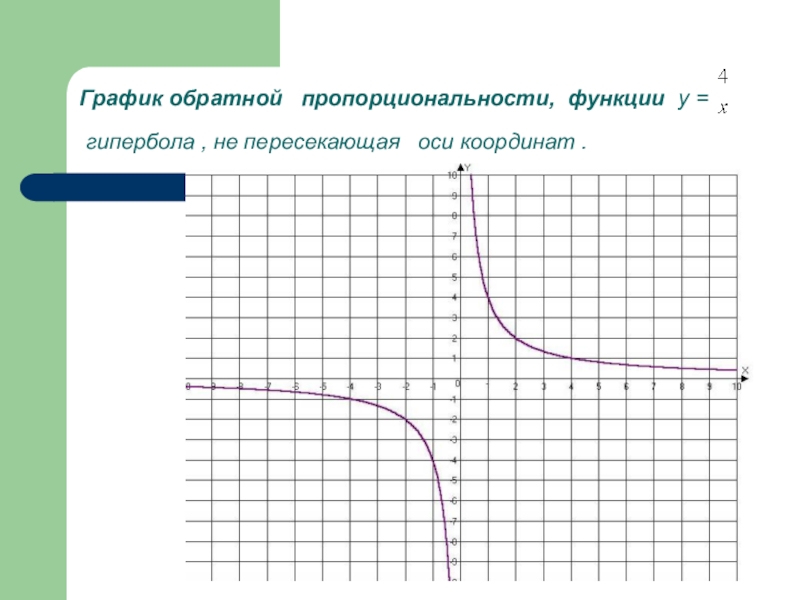
- 5. График обратной пропорциональности, функции у =
- 6. График квадратичной функции
- 7. График кубической функции y
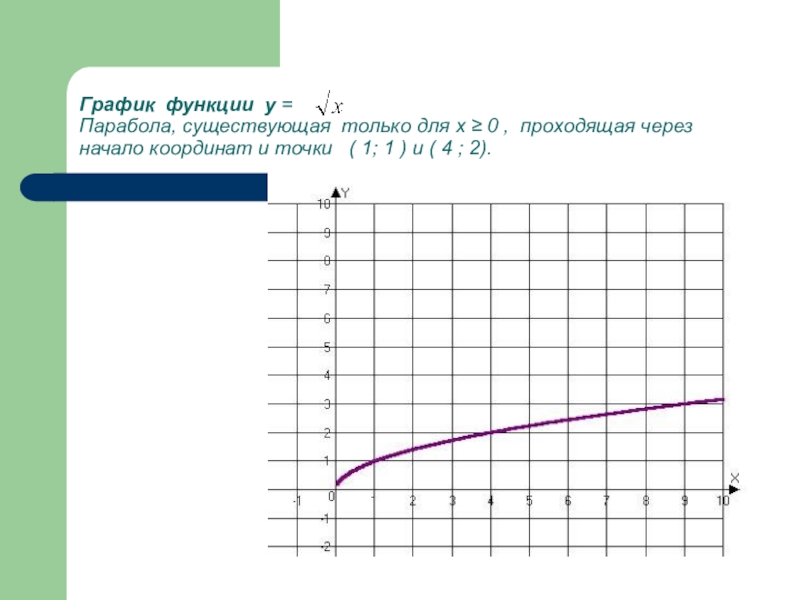
- 8. График функции y = Парабола, существующая
- 9. Теперь повторим материал 8 класса по уравнению
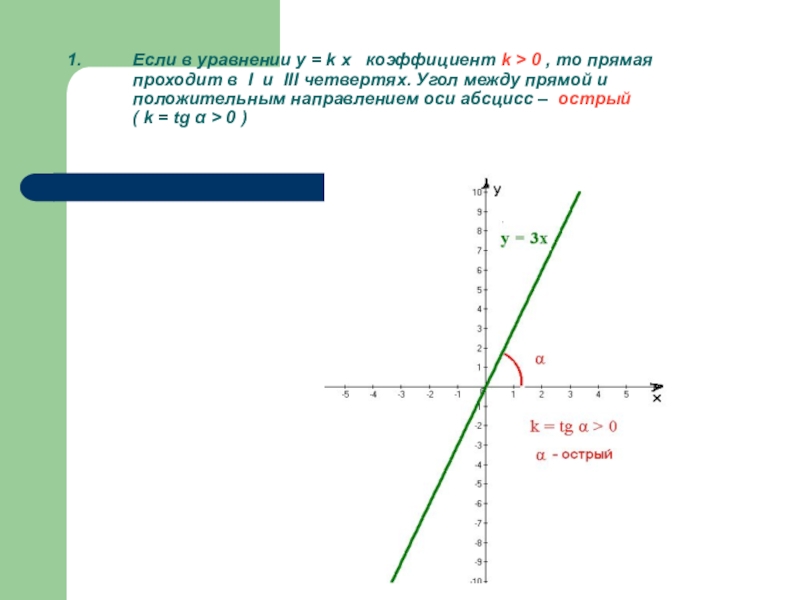
- 10. Если в уравнении y = k x
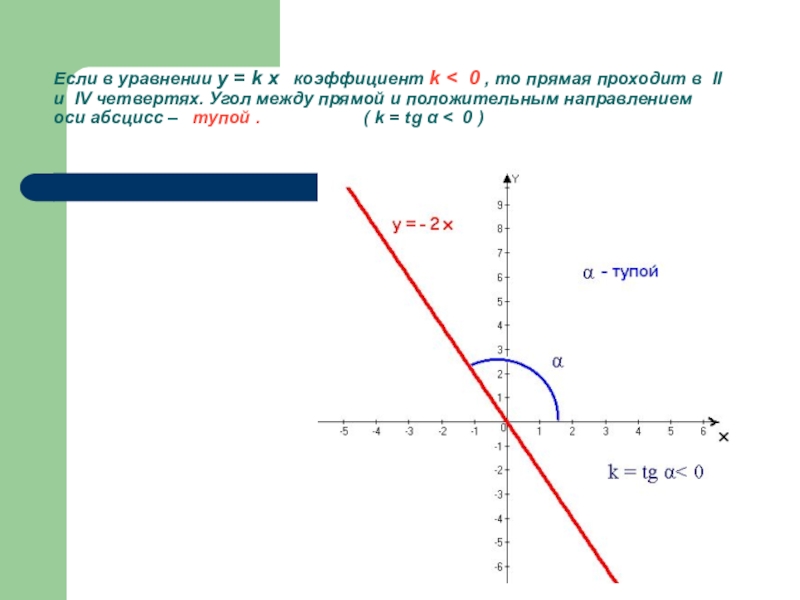
- 11. Если в уравнении y = k x
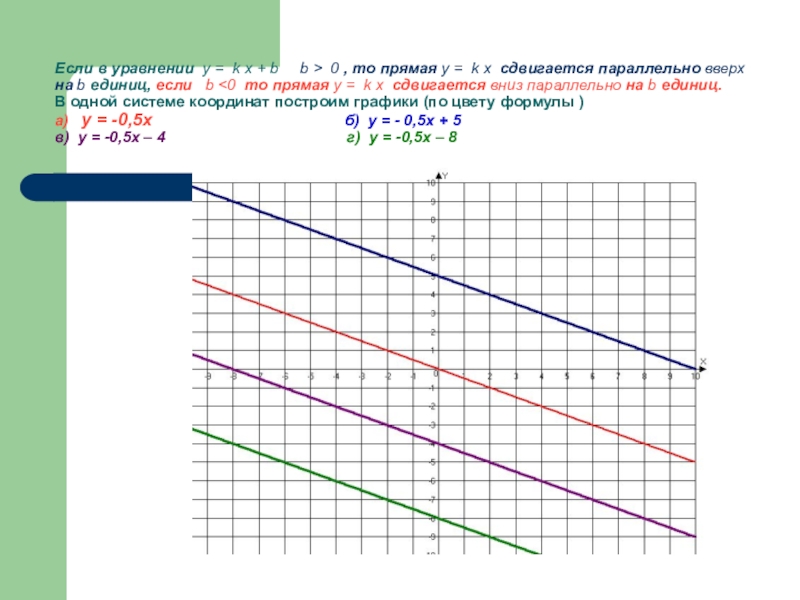
- 12. Если в уравнении y = k x
- 13. Рассмотрим, какова роль свободного члена b в
- 14. Мы всё ближе к осознанию преобразования графика
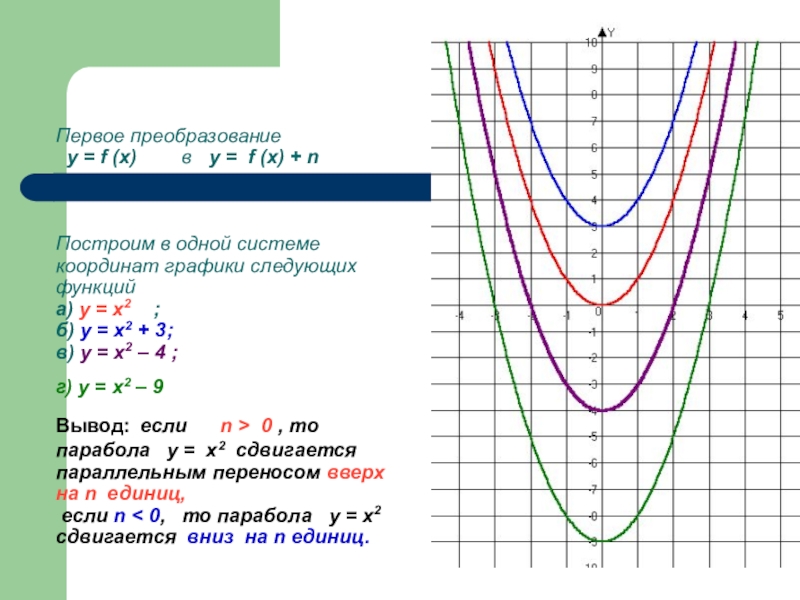
- 15. Первое преобразование у =
- 16. Рассмотрим преобразование, которое мы не могли наблюдать
- 17. Для того, чтобы увидеть параллельный перенос –
- 18. Теперь рассмотрим преобразование у
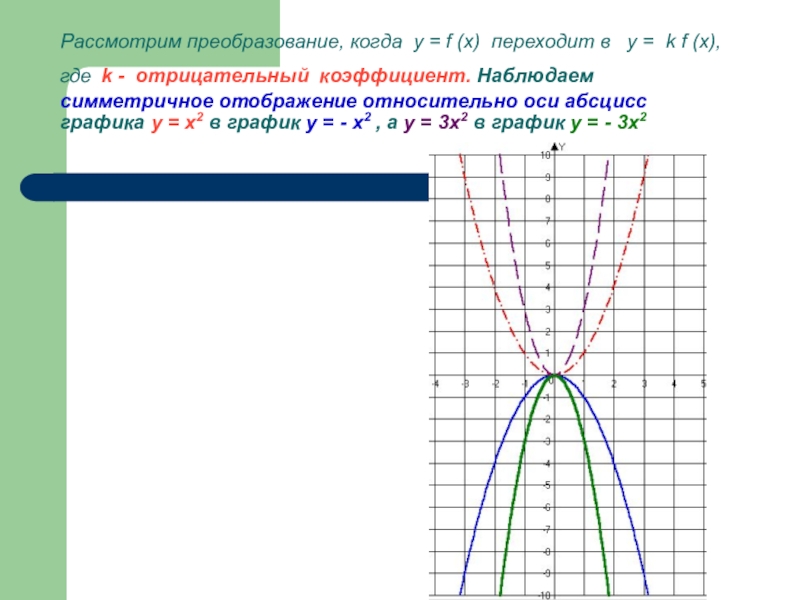
- 19. Рассмотрим преобразование, когда у = f (x)
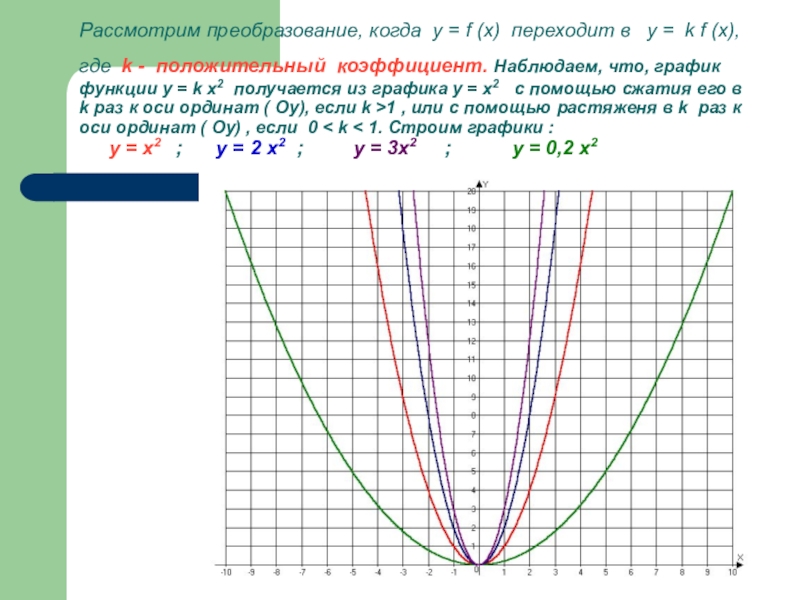
- 20. Рассмотрим преобразование, когда у = f (x)
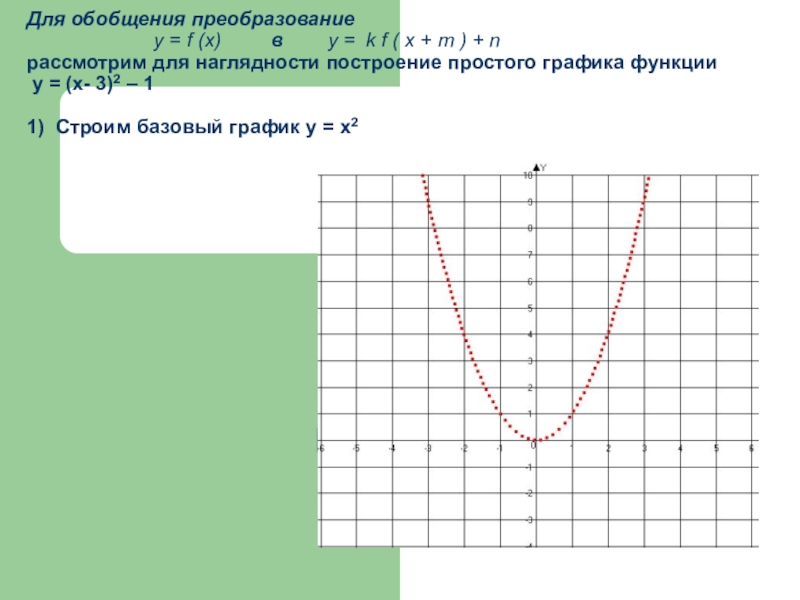
- 21. Для обобщения преобразование
- 22. Слайд 22
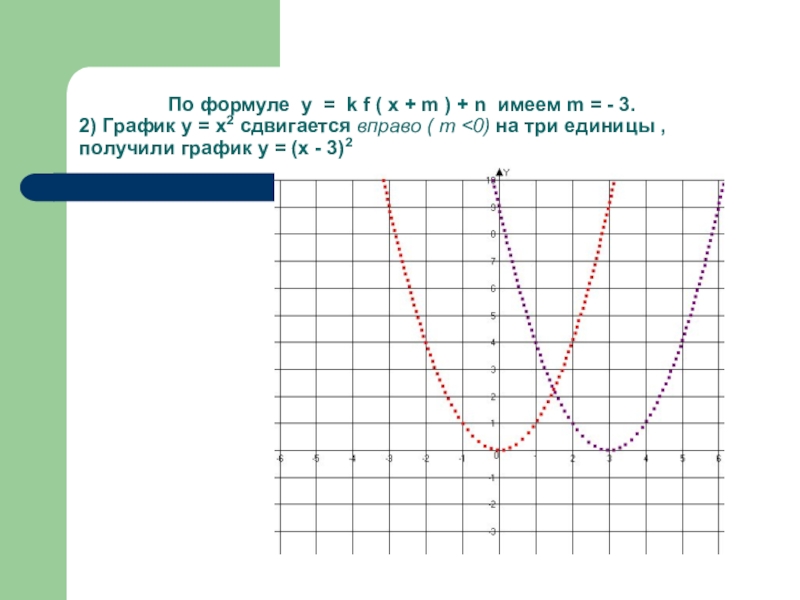
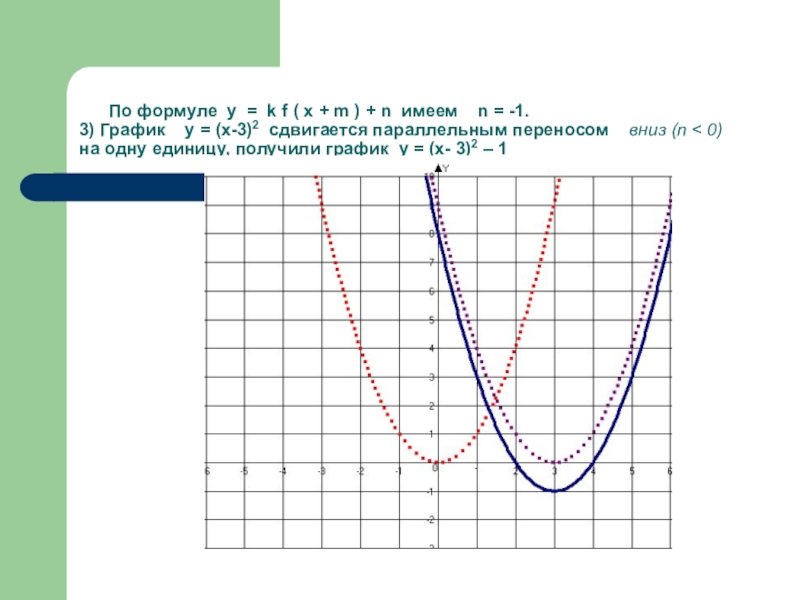
- 23. По формуле у =
- 24. Подведем итоговое преобразование, комплексно объединяющее
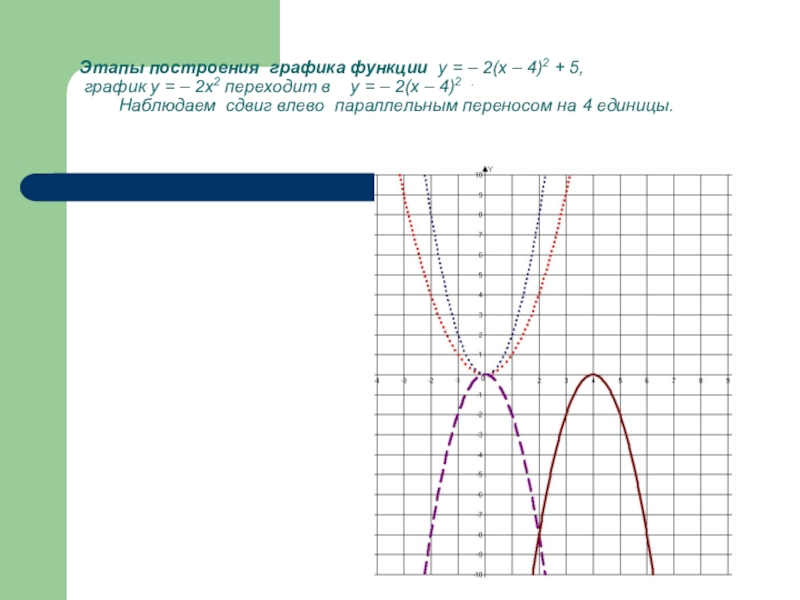
- 25. Этапы построения графика функции у =
- 26. Этапы построения графика функции у = –
- 27. Этапы построения графика функции у = –
- 28. Этапы построения графика функции у = –
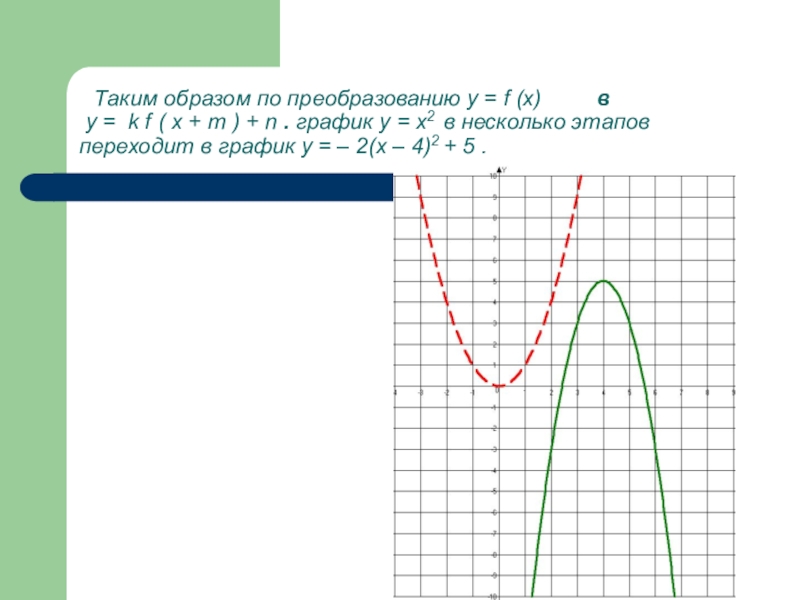
- 29. Таким образом по преобразованию у
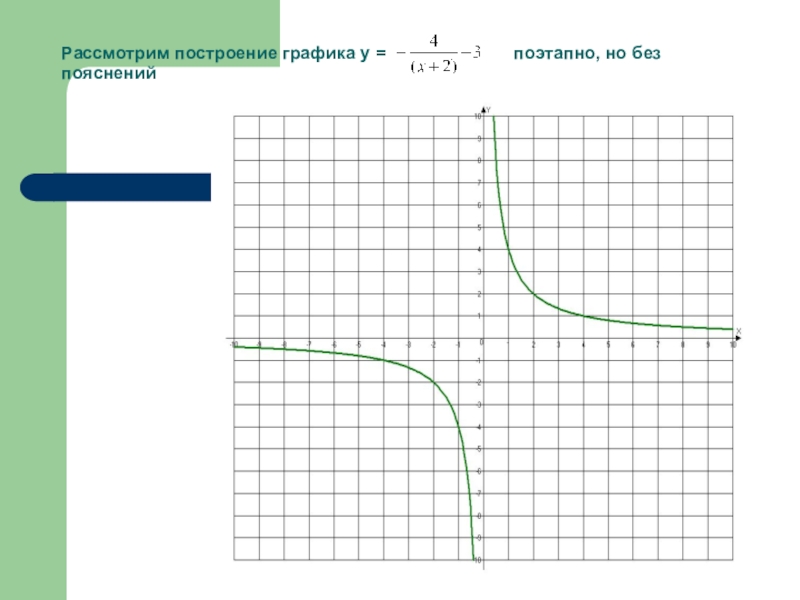
- 30. Рассмотрим построение графика у =
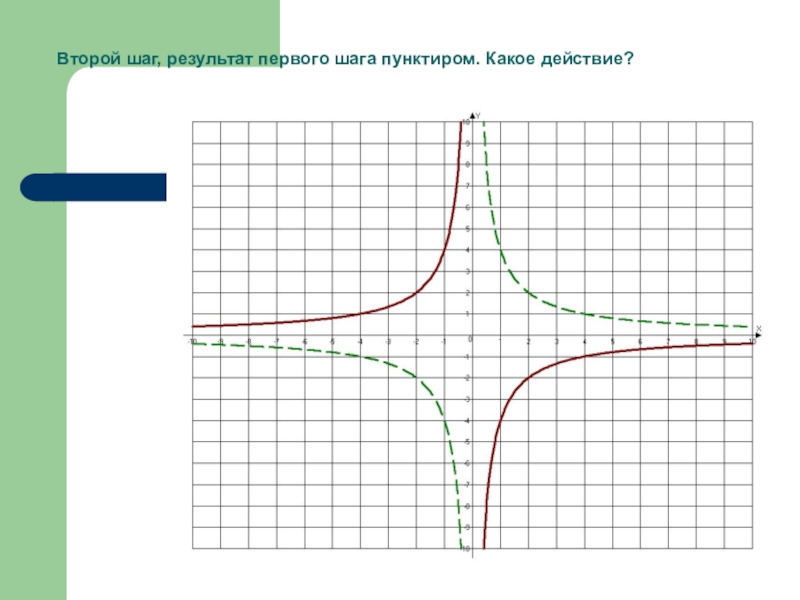
- 31. Второй шаг, результат первого шага пунктиром. Какое действие?
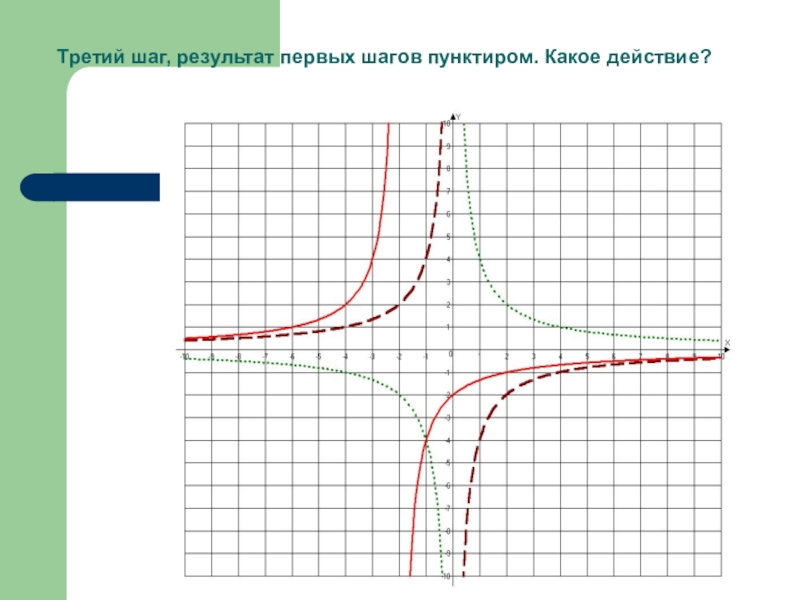
- 32. Третий шаг, результат первых шагов пунктиром. Какое действие?
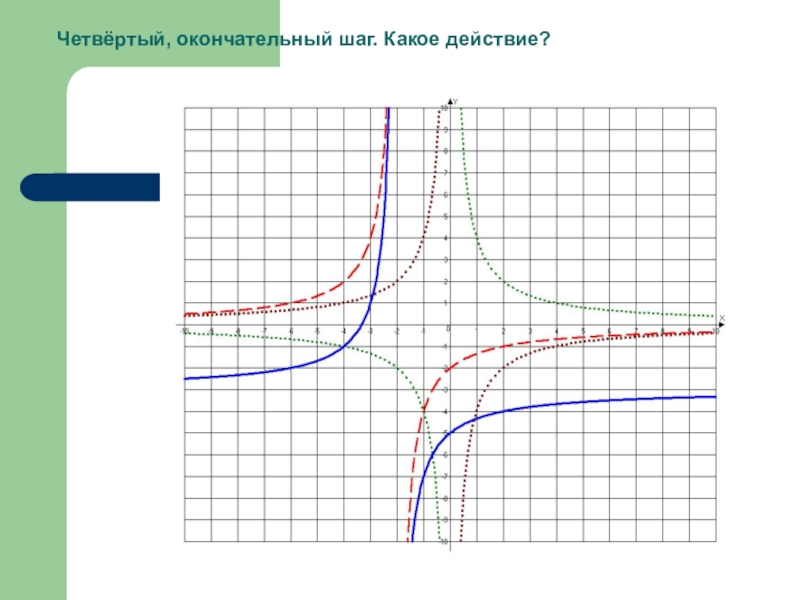
- 33. Четвёртый, окончательный шаг. Какое действие?
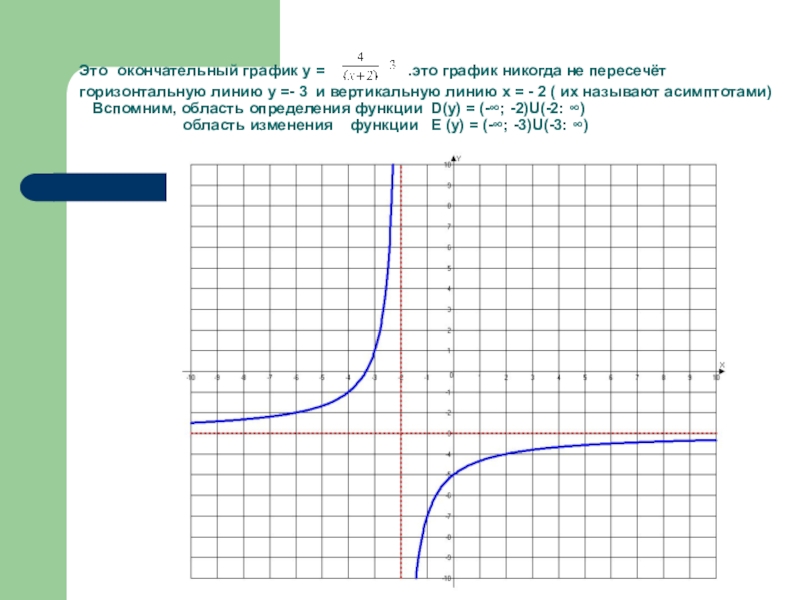
- 34. Это окончательный график у =
- 35. В преобразовании у = f (x)
- 36. Слайд 36
- 37. Проверьте степень усвоения учебного материала, ответив на
- 38. B-1 русский язB-2 украинский язык
- 39. Проверим результаты усвоения материала
- 40. B-1B-2
- 41. Удачи и терпения в
Рассмотрим преобразования графика функции у = f (x) в график функции у = k f ( x + m ) + n . Осознаем роль коэффициента k и слагаемых m и n
Слайд 1 Презентация – пособие «Преобразование графиков функций »
Часть I
Слайд 2 Рассмотрим преобразования графика функции у = f (x) в
график функции у = k f ( x + m ) + n .
Осознаем роль коэффициента k и слагаемых m и n в данной формуле.
График функции у = f (x) является базовым. Повторим для начала все основные графики функций, которые мы изучали в 9 классе
Слайд 3Прямая пропорциональность y = k x Например, у = 2х
, (прямая, проходящая через начало координат.)
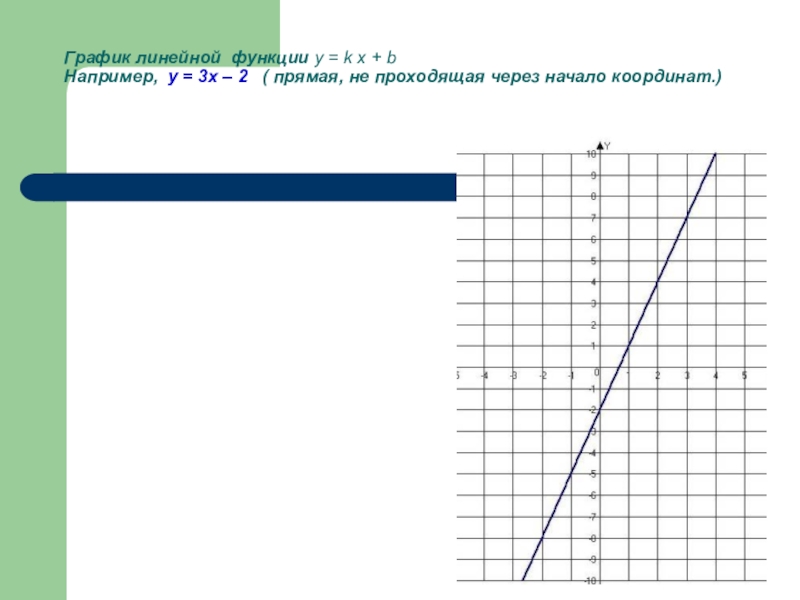
Слайд 4График линейной функции y = k x + b Например, у =
3х – 2 ( прямая, не проходящая через начало координат.)
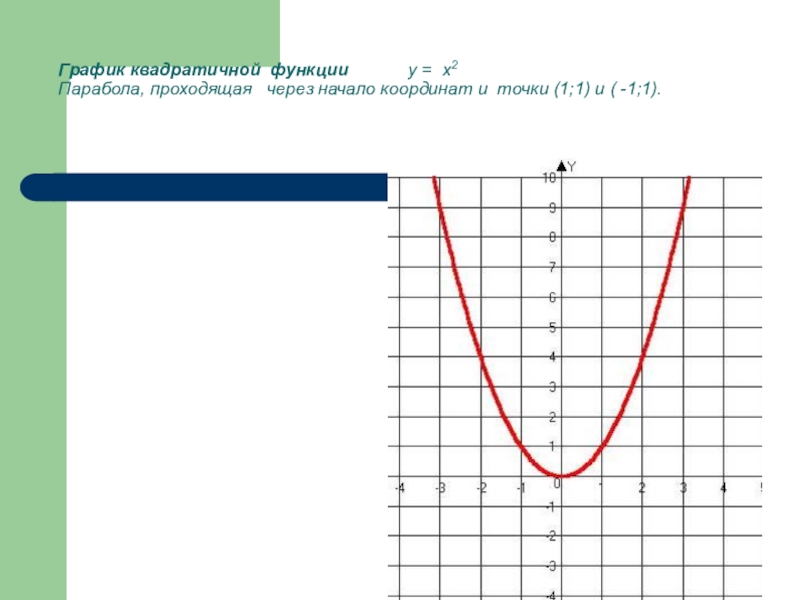
Слайд 6График квадратичной функции y = x2 Парабола,
проходящая через начало координат и точки (1;1) и ( -1;1).
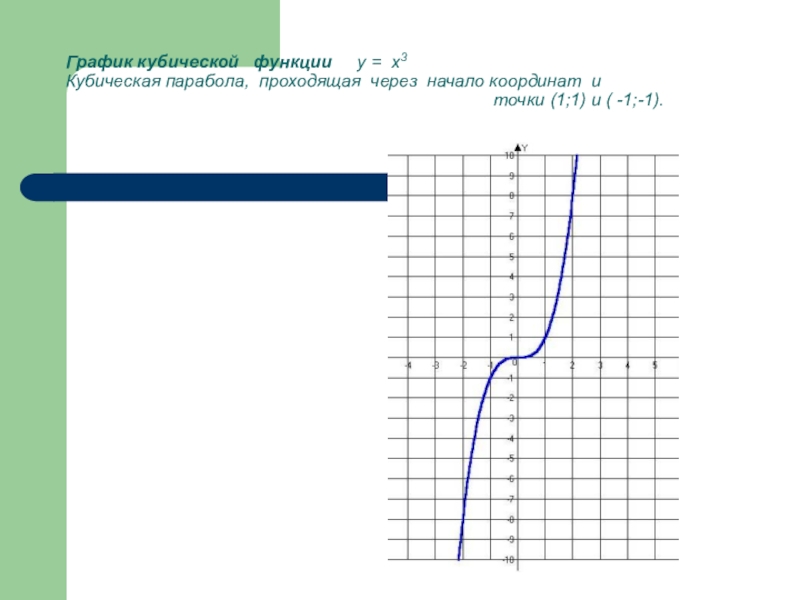
Слайд 7График кубической функции y = x3 Кубическая парабола, проходящая
через начало координат и
точки (1;1) и ( -1;-1).
Слайд 8График функции y = Парабола, существующая только для х ≥ 0
, проходящая через начало координат и точки ( 1; 1 ) и ( 4 ; 2).
Слайд 9Теперь повторим материал 8 класса по уравнению прямой
y = k∙x + b
Как проходит прямая в зависимости от коэффициента k ?
Каково положение прямой в зависимости от свободного члена b ?
Рассмотрим на конкретных примерах.
Слайд 10Если в уравнении y = k x коэффициент k >
0 , то прямая проходит в I и III четвертях. Угол между прямой и положительным направлением оси абсцисс – острый
( k = tg α > 0 )
Слайд 11Если в уравнении y = k x коэффициент k
0 , то прямая проходит в II и IV четвертях. Угол между прямой и положительным направлением оси абсцисс – тупой . ( k = tg α < 0 )
Слайд 12Если в уравнении y = k x + b
b > 0 , то прямая y = k x сдвигается параллельно вверх на b единиц, если b <0 то прямая y = k x сдвигается вниз параллельно на b единиц.
В одной системе координат построим графики (по цвету формулы )
а) у = -0,5х б) у = - 0,5х + 5
в) у = -0,5х – 4 г) у = -0,5х – 8
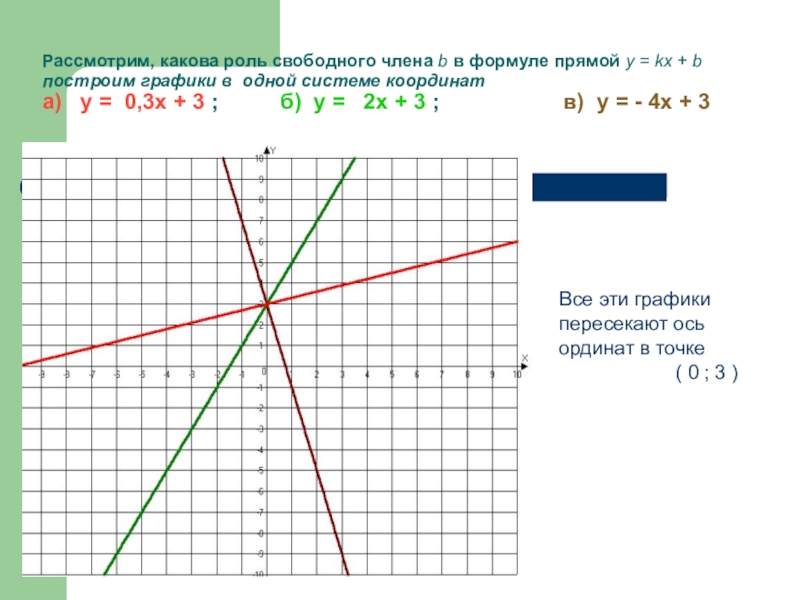
Слайд 13Рассмотрим, какова роль свободного члена b в формуле прямой у =
kx + b
построим графики в одной системе координат
а) у = 0,3х + 3 ; б) у = 2х + 3 ; в) у = - 4х + 3
Все эти графики пересекают ось ординат в точке
( 0 ; 3 )
Слайд 14Мы всё ближе к осознанию преобразования графика функции у
= f (x) в график функции
у = k f ( x + m ) + n
Рассмотрим поэтапно преобразования:
а) f (x) и f (x) + n
б) f (x) и f ( x + m)
в) f (x) и k f (x)
г) f (x) и k f ( x + m ) + n
Слайд 15Первое преобразование у = f (x)
в у = f (x) + n
Построим в одной системе координат графики следующих функций
а) у = х2 ; б) у = х2 + 3;
в) у = х2 – 4 ;
г) у = х2 – 9
Вывод: если n > 0 , то парабола y = x2 сдвигается параллельным переносом вверх на n единиц,
если n < 0, то парабола y = x2 сдвигается вниз на n единиц.
Слайд 16Рассмотрим преобразование, которое мы не могли наблюдать с графиками прямых. Общий
вид преобразования у = f (x) и у = f ( x + m). Теперь число прибавляется не к функции, как в предыдущем примере, а к аргументу.
Что же мы ожидаем увидеть?
Что если m > 0 , то парабола y = x2 сдвигается параллельным переносом вдоль оси абсцисс влево на m единиц, если m <0 то парабола y = x2 сдвигается параллельным переносом вдоль оси абсцисс вправо на m единиц.
То есть если m положительное число, то сдвиг происходит вдоль оси абсцисс , но в отрицательном направлении и , наоборот, если m отрицательное число, то сдвиг происходит вдоль оси абсцисс , но в положительном направлении
Слайд 17Для того, чтобы увидеть параллельный перенос – сдвиг вдоль оси абсцисс
нам достаточно построить в одной системе координат графики следующих функций
1. у = х2 ; 2. у =( х + 2)2;
3. у =( х – 3)2 ; 4. у =( х – 5)2
Слайд 18Теперь рассмотрим преобразование у = f (x) и
у = k f (x).
Оценим роль коэффициента k. Оценивать будем по двум моментам.
а) k - положительный или отрицательный коэффициент.
б) k - больше или меньше единицы.
Слайд 19Рассмотрим преобразование, когда у = f (x) переходит в у
= k f (x), где k - отрицательный коэффициент. Наблюдаем симметричное отображение относительно оси абсцисс графика у = х2 в график у = - х2 , а у = 3х2 в график у = - 3х2
Слайд 20Рассмотрим преобразование, когда у = f (x) переходит в у
= k f (x), где k - положительный коэффициент. Наблюдаем, что, график функции у = k х2 получается из графика у = х2 с помощью сжатия его в k раз к оси ординат ( Оу), если k >1 , или с помощью растяженя в k раз к оси ординат ( Оу) , если 0 < k < 1. Строим графики :
у = х2 ; у = 2 х2 ; у = 3х2 ; у = 0,2 х2
Слайд 21Для обобщения преобразование
у = f (x) в у = k f ( x + m ) + n
рассмотрим для наглядности построение простого графика функции
у = (х- 3)2 – 1
1) Строим базовый график у = х2
Слайд 22
По формуле у = k f ( x + m ) + n имеем m = - 3.
2) График у = х2 сдвигается вправо ( m <0) на три единицы , получили график у = (х - 3)2
Слайд 23 По формуле у = k f ( x
+ m ) + n имеем n = -1.
3) График у = (х-3)2 сдвигается параллельным переносом вниз (n < 0) на одну единицу, получили график у = (х- 3)2 – 1
Слайд 24 Подведем итоговое преобразование, комплексно объединяющее все предыдущие преобразования у
= f (x) в у = k f ( x + m ) + n .
Из выше сказанного, после обобщений, следует :
1) k – растягивает или сжимает график функции f (x) к оси ординат (Оу)
2) m – производит сдвиг графика вдоль оси абсцисс (Ох)
3) n – производит сдвиг графика вдоль оси ординат (Оу)
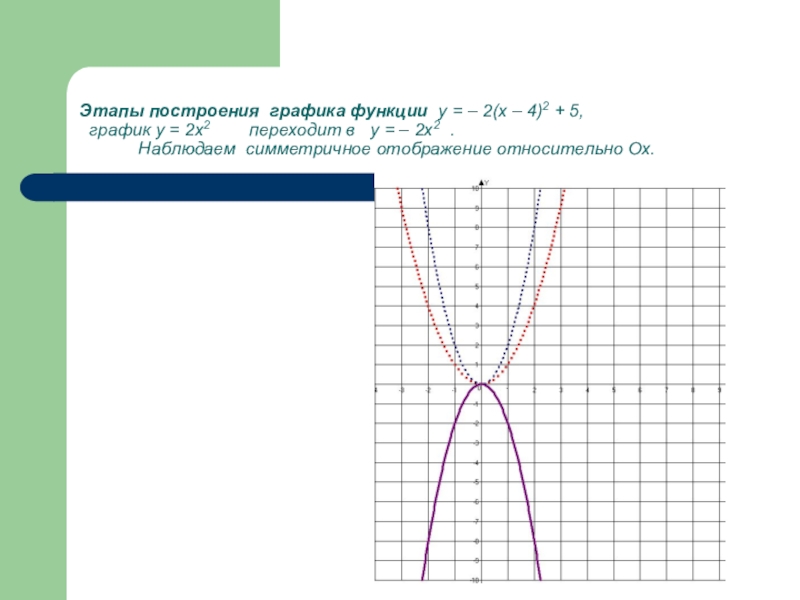
Для наглядности построим график функции у = – 2(х – 4)2 + 5, но разобьём построение на последовательные этапы
1. у = х2 (базовый график)
2. у = 2 х2 ( сжатие к оси ординат в два раза)
3. у = – 2х2 ( симметричное отображение относительно Ох)
4. у = – 2(х – 4)2 ( сдвиг влево на 4 единицы)
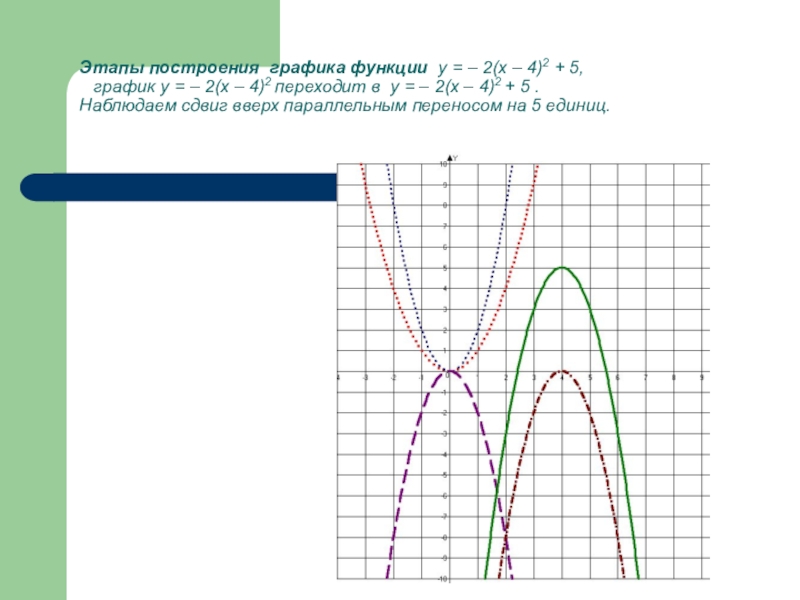
5. у = – 2(х – 4)2 + 5 (сдвиг вверх на 5 единиц)
Слайд 25 Этапы построения графика функции у = – 2(х – 4)2
+ 5,
базовый график у = х2 переходит в у = 2 х2 .
Наблюдаем сжатие к оси ординат (Оу) в два раза
Слайд 26Этапы построения графика функции у = – 2(х – 4)2 +
5,
график у = 2х2 переходит в у = – 2х2 .
Наблюдаем симметричное отображение относительно Ох.
Слайд 27Этапы построения графика функции у = – 2(х – 4)2 +
5,
график у = – 2х2 переходит в у = – 2(х – 4)2 .
Наблюдаем сдвиг влево параллельным переносом на 4 единицы.
Слайд 28Этапы построения графика функции у = – 2(х – 4)2 +
5,
график у = – 2(х – 4)2 переходит в у = – 2(х – 4)2 + 5 .
Наблюдаем сдвиг вверх параллельным переносом на 5 единиц.
Слайд 29 Таким образом по преобразованию у = f (x)
в
у = k f ( x + m ) + n . график у = х2 в несколько этапов переходит в график у = – 2(х – 4)2 + 5 .
Слайд 34Это окончательный график у = .это график
никогда не пересечёт горизонтальную линию у =- 3 и вертикальную линию х = - 2 ( их называют асимптотами)
Вспомним, область определения функции D(y) = (-∞; -2)U(-2: ∞)
область изменения функции Е (у) = (-∞; -3)U(-3: ∞)
Слайд 35 В преобразовании у = f (x) в у =
k f ( x + m ) + n не учитывается коэффициент, который может стоять перед аргументом Х. В 10 классе это будет учитываться.
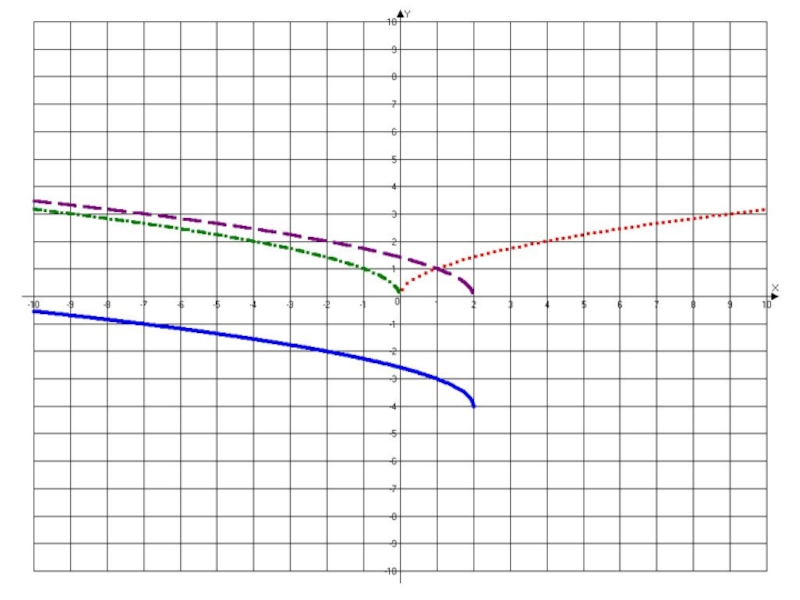
А пока рассмотрим построение графика у =
Область определения D(y)= [0;∞) базовой
функции y =
Минус перед аргументом делает область определения противоположной.
D(y)= (-∞;0] для функции y =
То есть происходит симметричное отображение базового графика, но относительно оси Оу.
Ну а дальнейшие преобразования - параллельный сдвиг вправо и вниз Вам уже известен.
Проследите самостоятельно эти этапы, но уже в одной системе координат.
Слайд 37Проверьте степень усвоения учебного материала, ответив на тесты. Нажмите клавишу Esc
и заполните тесты.
Сравните свои ответы с приведёнными ниже, если результат Вас не удовлетворил, то посмотрите презентацию вновь, но более внимательно
Слайд 41Удачи и терпения в изучении
математики !!!
Когда будете закрывать программу , пожалуйста,
не сохраняйте изменения.
