- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Презенация по алгебре Уравнение у= х^2
Содержание
- 1. Презенация по алгебре Уравнение у= х^2
- 2. Слайд 2
- 3. Рассмотрим уравнение х2= aa – некоторое числох - переменная
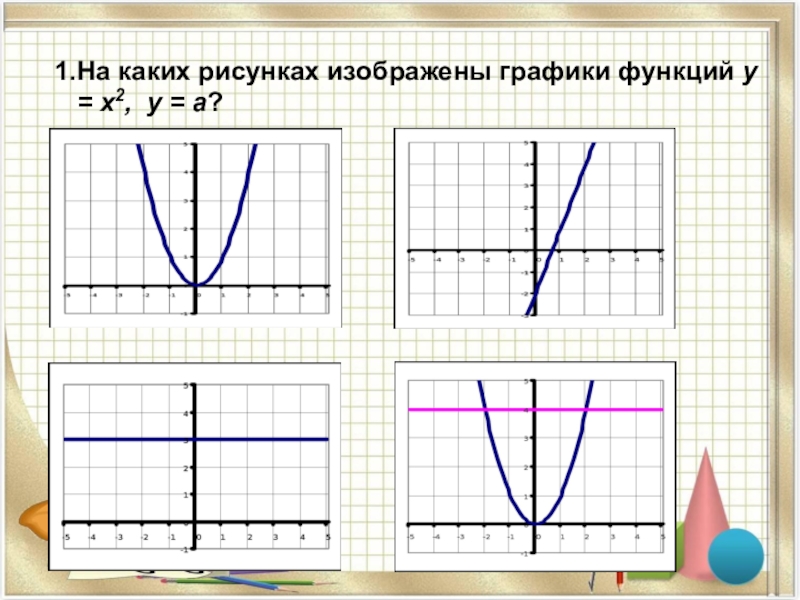
- 4. На каких рисунках изображены графики функций у = х2, у = а?
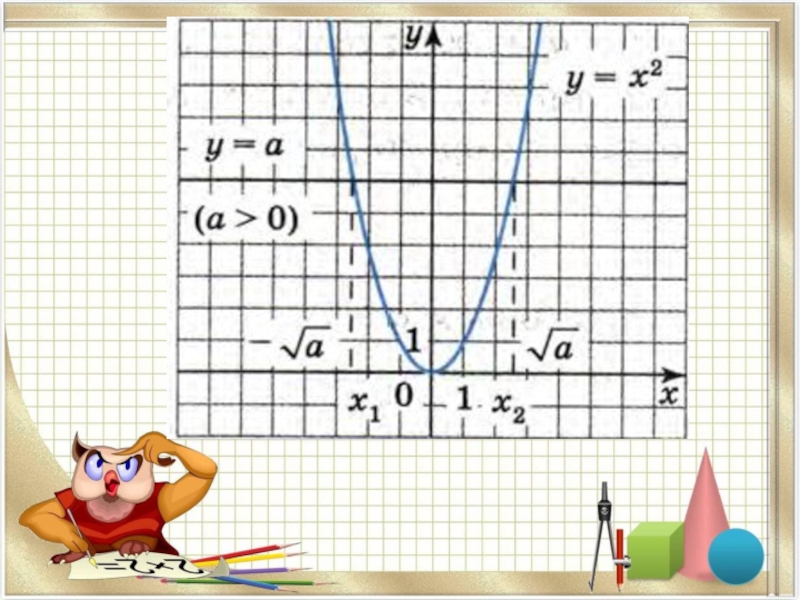
- 5. Рассмотрим графическое решение
- 6. Слайд 6
- 7. Слайд 7
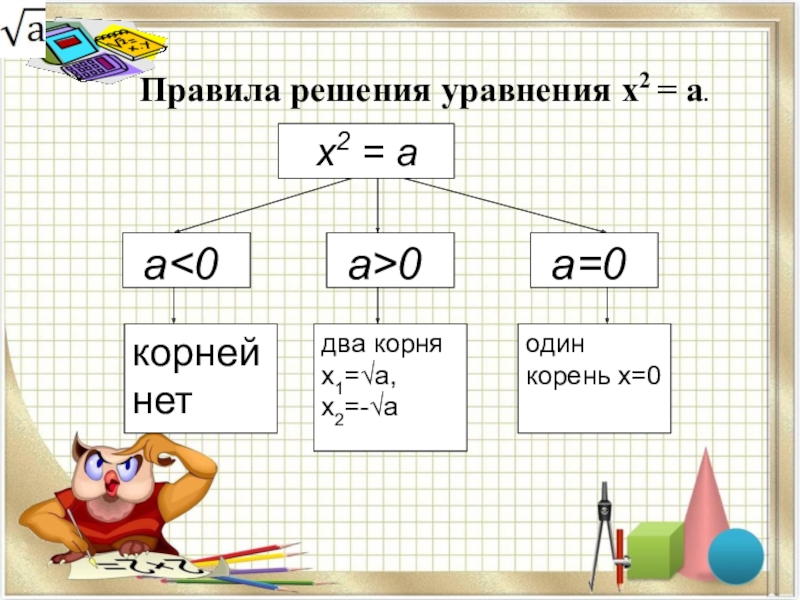
- 8. Правила решения уравнения х2 = а.
- 9. Нахождение приближенных значений квадратного корня
- 10. ПОВТОРЕНИЕ ВЫЧИСЛИТЕ √25 =√16 = √9 = 5 4 3√81 =√2 = 9?
- 11. Извлекается √2 нацело? Нет. Как будем находить?Какие знаем способы нахождения корней?
- 12. 1 МЕТОД вычислить √2 с
- 13. Слайд 13
- 14. Теперь попытаемся отыскать цифру десятых. Для этого будем
- 15. Получили число превышающее двойку, остальные числа уже
- 16. Слайд 16
- 17. Далее ищем цифру сотых, точно таким же образом.
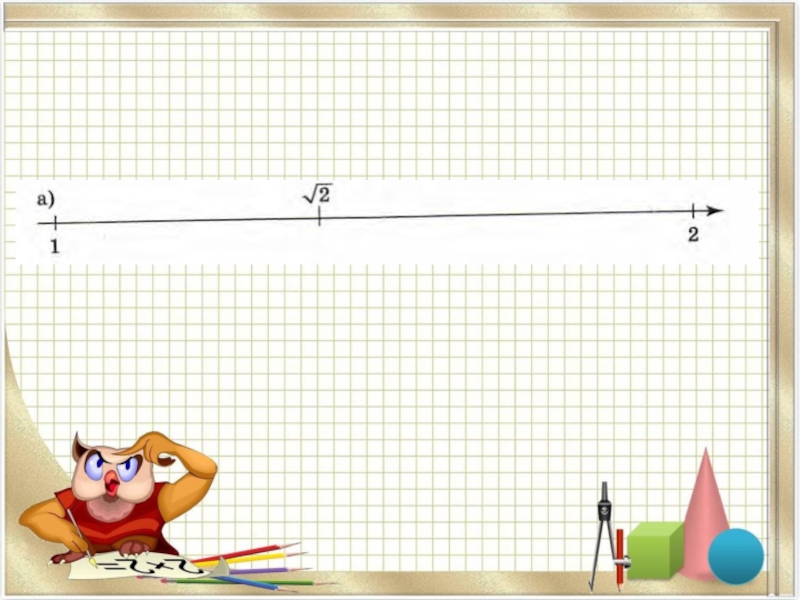
- 18. Из этого получаем, что число √2 будет принадлежать промежутку от 1,41 до 1,42 (1,41< √2
- 19. Слайд 19
- 20. Вывод Данный прием позволяет извлекать корень с любой заданной наперед точностью.
- 21. 2 МЕТОД Чтобы узнать целую часть
- 22. 2 МЕТОД Чтобы узнать целую часть
- 23. Вывод Данный прием удобен тогда, когда корень извлекается нацело.
- 24. Слайд 24
- 25. Интернет-ресурсыКарандаши Мудрая сова Циркуль Фон "тетрадная клетка"
Рассмотрим уравнение х2= aa – некоторое числох - переменная
Слайд 12 1 МЕТОД вычислить √2 с точностью до двух знаков
после запятой
Будем рассуждать следующим образом.
Число √2 больше 1, так как 12 < 2. В тоже время, число √2 < 2, так как 22 больше 2.
Следовательно, десятичная запись числа будет начинаться следующим образом: 1,… То есть корень из двух, это единица с чем-то.
1< √2 < 2.
Будем рассуждать следующим образом.
Число √2 больше 1, так как 12 < 2. В тоже время, число √2 < 2, так как 22 больше 2.
Следовательно, десятичная запись числа будет начинаться следующим образом: 1,… То есть корень из двух, это единица с чем-то.
1< √2 < 2.
Слайд 14Теперь попытаемся отыскать цифру десятых.
Для этого будем дроби от единицы до
двойки возводить в квадрат, пока не получим число большее двух.
Шаг деления возьмем 0,1, так как мы ищем число десятых.
Другими словами будем возводить в квадрат числа: 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9
1,12 =1,21; 1,22=1,44; 1,32=1,69; 1,42=1,96; 1,52=2,25.
Шаг деления возьмем 0,1, так как мы ищем число десятых.
Другими словами будем возводить в квадрат числа: 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9
1,12 =1,21; 1,22=1,44; 1,32=1,69; 1,42=1,96; 1,52=2,25.
Слайд 15Получили число превышающее двойку, остальные числа уже не надо возводить в
квадрат.
Число 1,42 меньше 2, а 1,52 уже больше двух, то число √2 должно принадлежать промежутку от 1,4 до 1,5 . Следовательно, десятичная запись числа √2 в разряде десятых должна содержать 4.
Иначе говоря , √2=1,4… .
, 1,4< √2 < 1,5
Число 1,42 меньше 2, а 1,52 уже больше двух, то число √2 должно принадлежать промежутку от 1,4 до 1,5 . Следовательно, десятичная запись числа √2 в разряде десятых должна содержать 4.
Иначе говоря , √2=1,4… .
, 1,4< √2 < 1,5
Слайд 17Далее ищем цифру сотых, точно таким же образом. Возводим в квадрат числа
от 1,41 до 1,49, с шагом 0,01, пока не получим число большее двух.
1,412 =1,9881, 1,422=2,0164.
Уже при 1.42 получаем, что его квадрат больше двух, далее возводить в квадрат числа не имеет смысла.
1,412 =1,9881, 1,422=2,0164.
Уже при 1.42 получаем, что его квадрат больше двух, далее возводить в квадрат числа не имеет смысла.
Слайд 18Из этого получаем, что число √2 будет принадлежать промежутку от 1,41
до 1,42 (1,41< √2<1,42)
Так как нам необходимо записать √2 с точностью до двух знаков после запятой, то мы уже можем остановиться и не продолжать вычисления.
√2 ≈ 1,41. Это и будет ответом. Если бы необходимо было вычислить еще более точное значение, нужно было бы продолжать вычисления, повторяя снова и снова цепочку рассуждений.
Так как нам необходимо записать √2 с точностью до двух знаков после запятой, то мы уже можем остановиться и не продолжать вычисления.
√2 ≈ 1,41. Это и будет ответом. Если бы необходимо было вычислить еще более точное значение, нужно было бы продолжать вычисления, повторяя снова и снова цепочку рассуждений.
Слайд 212 МЕТОД Чтобы узнать целую часть квадратного корня числа, можно,
вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, посчитать количество выполненных действий.
Например, найдем √16 так:
16 - 1 = 15
15 - 3 = 12
12 - 5 = 7
7 - 7 =0
Выполнено 4 действия, значит,
√16 = 4
Например, найдем √16 так:
16 - 1 = 15
15 - 3 = 12
12 - 5 = 7
7 - 7 =0
Выполнено 4 действия, значит,
√16 = 4
Слайд 222 МЕТОД Чтобы узнать целую часть квадратного корня числа, можно,
вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, посчитать количество выполненных действий.
Например, найдем √16 так:
16 - 1 = 15
15 - 3 = 12
12 - 5 = 7
7 - 7 =0
Выполнено 4 действия, значит,
√16 = 4
Например, найдем √16 так:
16 - 1 = 15
15 - 3 = 12
12 - 5 = 7
7 - 7 =0
Выполнено 4 действия, значит,
√16 = 4
Слайд 25Интернет-ресурсы
Карандаши
Мудрая сова
Циркуль
Фон "тетрадная клетка"
источник шаблона:
Ранько Елена
Алексеевна
учитель начальных классов
МАОУ лицей №21
г. Иваново
учитель начальных классов
МАОУ лицей №21
г. Иваново