- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Построение графика квадратичной функции
Содержание
- 1. Построение графика квадратичной функции
- 2. Цели урока: Образовательные: научиться построению графика квадратичной
- 3. Квадратичной функцией называется функция, которую можно задать
- 4. Графиком квадратичной функции является парабола, ветви которой
- 5. Чтобы построить график функции надо:1. Описать функцию:
- 6. Чтобы построить график функции надо:2. Найти координаты
- 7. Чтобы построить график функции надо:3. Заполнить таблицу
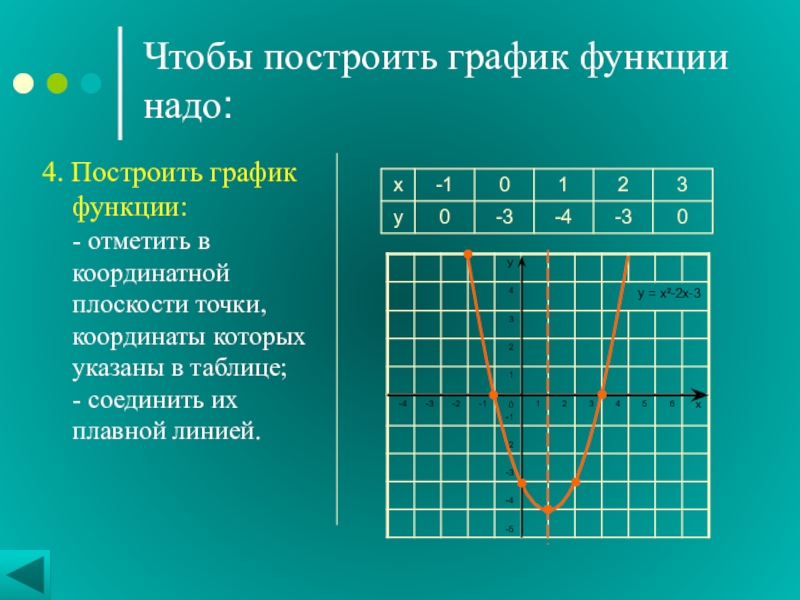
- 8. Чтобы построить график функции надо:4. Построить график
- 9. Сформулируйте определение квадратичной функции.Что представляет собой график
- 10. Попробуйте построить в тетради график функции у
- 11. Постройте график функции у = -2х²+8х-3
- 12. Проверьте себя. Ваше задание должно быть выполнено
- 13. Рассмотрим свойства этой квадратичной функции. Область
- 14. Выполните следующую работу в тетрадях по вариантам.
- 15. Домашнее задание: Пункт 7. стр44-46ЗНАТЬ наизусть АЛГОРИТМ построения квадратичной функции № 121, № 132
Слайд 1«Построение графика квадратичной функции»
Подготовила: Соколова Н.С., учитель математики, первой квалификационной категории
Слайд 2Цели урока:
Образовательные: научиться построению графика квадратичной функции и использованию графика
Развивающие: развивать логическое мышление, алгоритмическую культуру, внимание, навыки самостоятельной работы с источником информации и самоконтроля, поддерживать интерес к математике.
Воспитательные: воспитывать последовательность, ответственность, самостоятельность, настойчивость, дисциплинированность.
Слайд 3Квадратичной функцией называется функция, которую можно задать формулой вида y=ax²+bx+c, где
Слайд 4Графиком квадратичной функции является парабола, ветви которой направлены вверх(если а>0)
Например:
у=2х²+4х-1 – графиком является парабола, ветви которой направлены вверх (т.к. а=2, а>0).
у= -7х²-х+3 – графиком является парабола, ветви которой направлены вниз (т.к. а=-7, а<0).
у
0
х
у
0
х
Слайд 5Чтобы построить график функции надо:
1. Описать функцию:
название функции,
что является графиком
куда направлены ветви параболы.
Пример: у = х²-2х-3 – квадратичная функция, графиком является парабола, ветви которой направлены вверх (т.к. а=1, а>0)
Слайд 6Чтобы построить график функции надо:
2. Найти координаты вершины параболы А(m;n) по
;
или n = у(m) т.е. подставить найденное значение абсциссы m в формулу, которой задана функция и вычислить значение.
Прямая x=m является осью симметрии параболы.
Пример: у = х²-2х-3 (а = 1; b = -2; с = -3) Найдём координаты вершины параболы
n = 1²-2·1-3 = -4
А(1;-4) – вершина параболы.
х=1 – ось симметрии параболы.
Слайд 7Чтобы построить график функции надо:
3. Заполнить таблицу значений функции:
Прямая x=m
В таблице расположить вершину в середине таблицы и взять соседние симметричные значения х. Например, следующим образом:
*- посчитать значение функции в выбранных значениях х.
Пример: у = х²-2х-3
А(1;- 4) – вершина параболы
х=1 – ось симметрии параболы.
Составим таблицу значений функции:
Слайд 8Чтобы построить график функции надо:
4. Построить график функции:
Слайд 9Сформулируйте определение квадратичной функции.
Что представляет собой график квадратичной функции?
Куда могут быть
В какой последовательности нужно строить график квадратичной функции?
Попробуйте ответить на контрольные вопросы:
Слайд 10
Попробуйте построить в тетради график функции
у = -2х²+8х-3
Если вы забыли
Слайд 11Постройте график функции у = -2х²+8х-3
План построения графика квадратичной функции:
1.
название функции;
что является графиком функции;
куда направлены ветви параболы
2. Найти координаты вершины параболы А(m;n)
по формулам:
или n = у(m)
3. Заполнить таблицу значений функции.
4. Построить график функции:
отметить в координатной плоскости точки, координаты которых указаны в таблице;
соединить их плавной линией.
Слайд 12Проверьте себя. Ваше задание должно быть выполнено следующим образом:
у = -2х²+8х-3
Найдём координаты вершины параболы
n = -2·2²+8·2-3 =5
А ( 2; 5 ) – вершина параболы.
х=5 ось симметрии параболы.
Составим таблицу значений функции.
Слайд 13Рассмотрим свойства этой квадратичной функции.
Область определения функции (-∞;+∞)
Область значений функции
Нули функции х=0,5 и х=3,5
у>0 на промежутке (0,5;3,5)
y<0 на каждом из промежутков (-∞;0,5) и (3,5;+∞)
Функция возрастает на промежутке (-∞;2]
функция убывает на промежутке [2;+∞)
Наибольшее значение функции равно 5
Слайд 14Выполните следующую работу в тетрадях по вариантам.
Постройте графики функций:
I вариант
у
Укажите ООФ, ОЗФ, нули функции, промежуток возрастания функции.
II вариант
у = -х²-6х-7
Укажите ООФ, ОЗФ, нули функции, промежуток убывания функции.











![Построение графика квадратичной функции Рассмотрим свойства этой квадратичной функции. Область определения функции (-∞;+∞) Область значений функции Рассмотрим свойства этой квадратичной функции. Область определения функции (-∞;+∞) Область значений функции (-∞;5]Нули функции х=0,5 и х=3,5у>0](/img/tmb/5/415195/a6485762c69893a311931a2e9d40c2cb-800x.jpg)







