Рашитовна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Площадь криволинейной трапеции и интеграл
Содержание
- 1. Площадь криволинейной трапеции и интеграл
- 2. Криволинейная трапецияОтрезок [a;b] называют основанием этой криволинейной
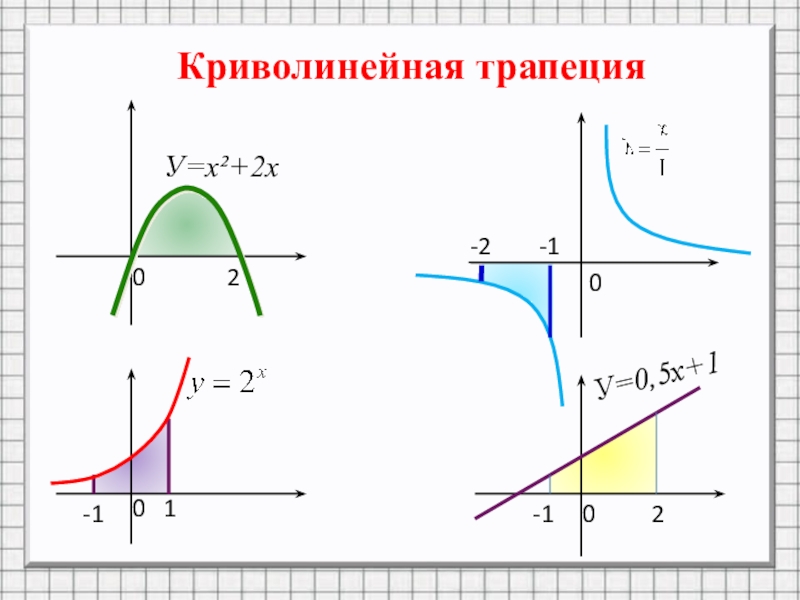
- 3. Криволинейная трапеция020001-1-12-1-2У=х²+2хУ=0,5х+1
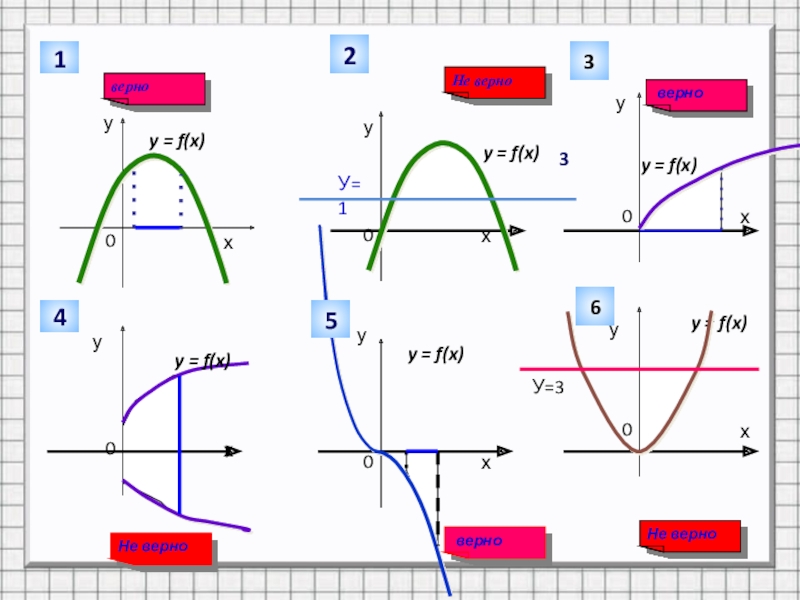
- 4. Какие из заштрихованных на рисунке фигур являются криволинейными трапециями, а какие нет?Заполнить таблицу
- 5. у1Не верноуууууУ=12верно33y = f(x)y = f(x)y =
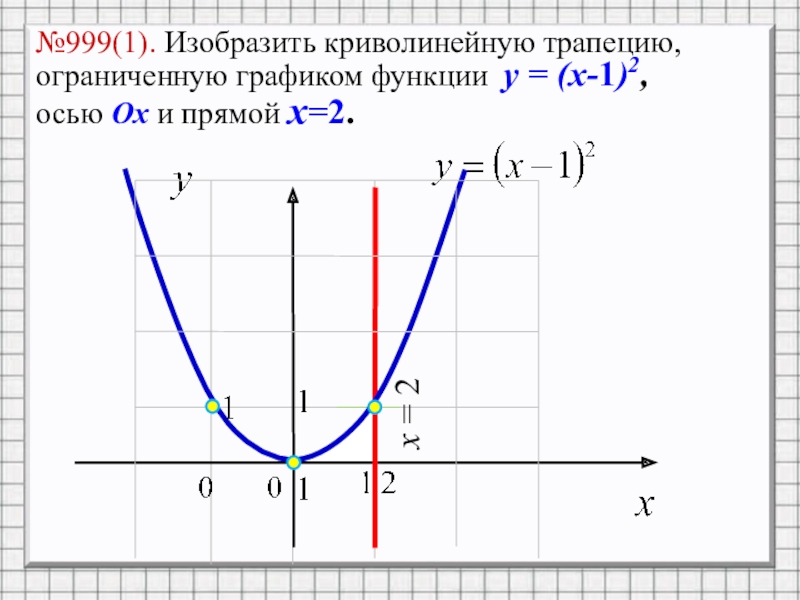
- 6. №999(1). Изобразить криволинейную трапецию, ограниченную графиком функции
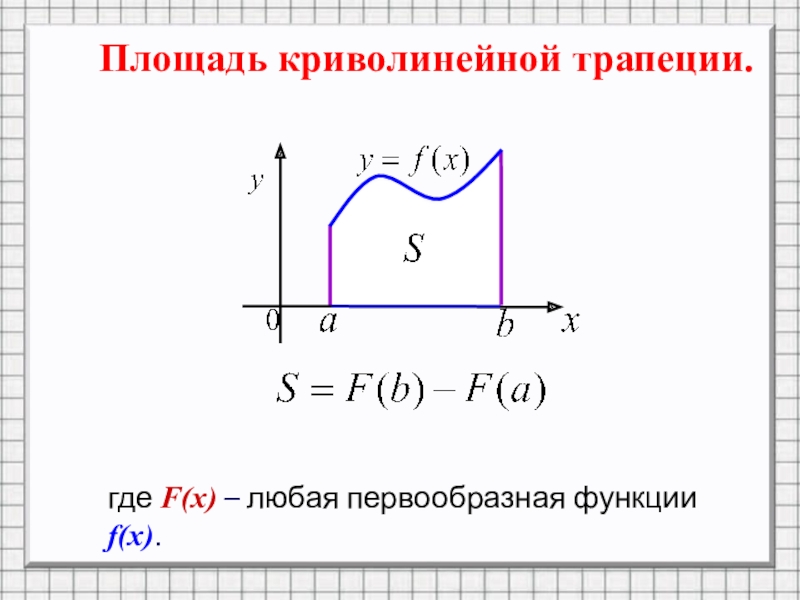
- 7. Площадь криволинейной трапеции.где F(x) – любая первообразная функции f(x).
- 8. Формула Ньютона-Лейбница1643—17271646—1716
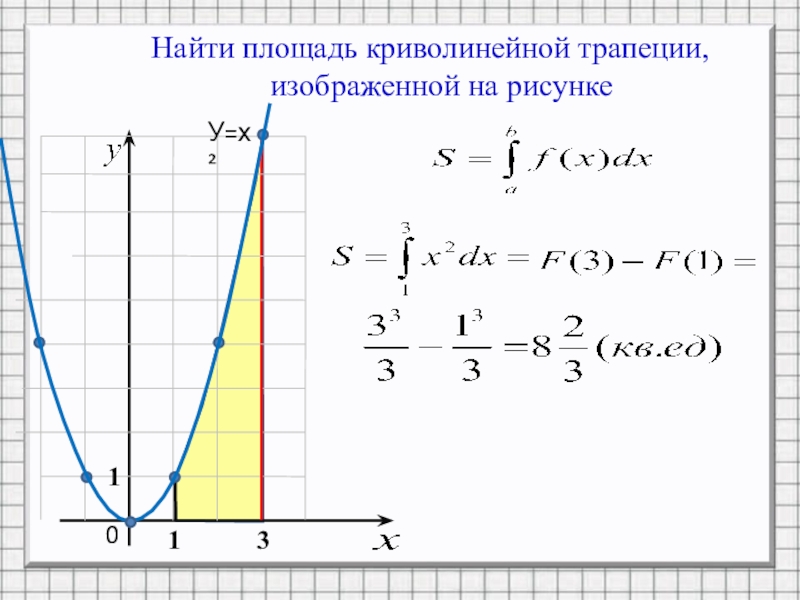
- 9. Найти площадь криволинейной трапеции, изображенной на рисунке013У=х²1
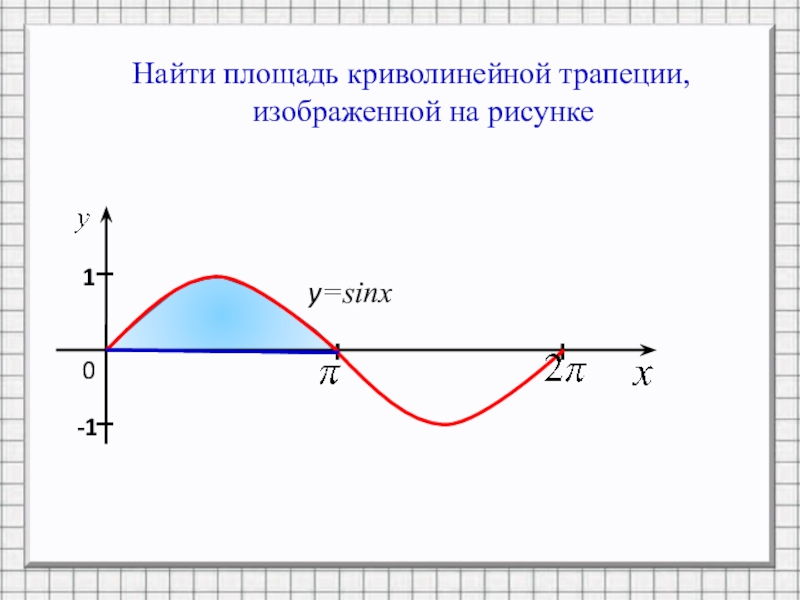
- 10. Найти площадь криволинейной трапеции, изображенной на рисунке0y=sinxII1-1
- 11. http://go.mail.ru/search_images?q=%источникиУчебник Алгебра и начала математического анализа 10-11 Ш.А.Алимов и дрhttp://go.mail.ru/search_images?q=%
Криволинейная трапецияОтрезок [a;b] называют основанием этой криволинейной трапецииКриволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющейна отрезке [а;b] знака функции f(х), прямымих=а, x=b и отрезком [а;b].
Слайд 1Площадь криволинейной трапеции и интеграл.
у
х
преподаватель математики КГА ПОУ ГАСКК МЦК
Филенко Юлия
Слайд 2Криволинейная трапеция
Отрезок [a;b] называют основанием
этой криволинейной трапеции
Криволинейной трапецией называется
фигура,
ограниченная графиком непрерывной и не меняющей
на отрезке [а;b] знака функции f(х), прямыми
х=а, x=b и отрезком [а;b].
ограниченная графиком непрерывной и не меняющей
на отрезке [а;b] знака функции f(х), прямыми
х=а, x=b и отрезком [а;b].
Слайд 4Какие из заштрихованных на рисунке фигур являются криволинейными трапециями, а какие
нет?
Заполнить таблицу
Слайд 5у
1
Не верно
у
у
у
у
у
У=1
2
верно
3
3
y = f(x)
y = f(x)
y = f(x)
y = f(x)
y =
f(x)
y = f(x)
У=3
4
5
6
Не верно
Не верно
верно
верно
Слайд 6№999(1). Изобразить криволинейную трапецию, ограниченную графиком функции y = (x-1)2, осью
Ox и прямой x=2.
x = 2
Слайд 11http://go.mail.ru/search_images?q=%
источники
Учебник Алгебра и начала математического анализа 10-11 Ш.А.Алимов
и др
http://go.mail.ru/search_images?q=%
![Площадь криволинейной трапеции и интеграл Криволинейная трапецияОтрезок [a;b] называют основанием этой криволинейной трапецииКриволинейной трапецией называется фигура, Криволинейная трапецияОтрезок [a;b] называют основанием этой криволинейной трапецииКриволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющейна](/img/thumbs/c23e7807a2d63f93351cca13f89a408d-800x.jpg)