- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Перпендикулярность прямой и плоскости.
Содержание
- 1. Перпендикулярность прямой и плоскости.
- 2. Перпендикулярные прямые в пространстве
- 3. Лемма о перпендикулярности двух прямых
- 4. Параллельные прямые, перпендикулярные к плоскости.Прямая называется перпендикулярной
- 5. Слайд 5
- 6. Слайд 6
- 7. Признак перпендикулярности прямой и плоскости.
- 8. Теорема о прямой, перпендикулярной к плоскости.
- 9. Перпендикуляр и наклонные. Угол между прямой и плоскостью.
- 10. Расстояние
- 11. Слайд 11
- 12. Слайд 12
- 13. Двугранный угол. Перпендикулярность плоскостей
- 14. Слайд 14
- 15. Слайд 15
- 16. Признак перпендикулярности двух
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
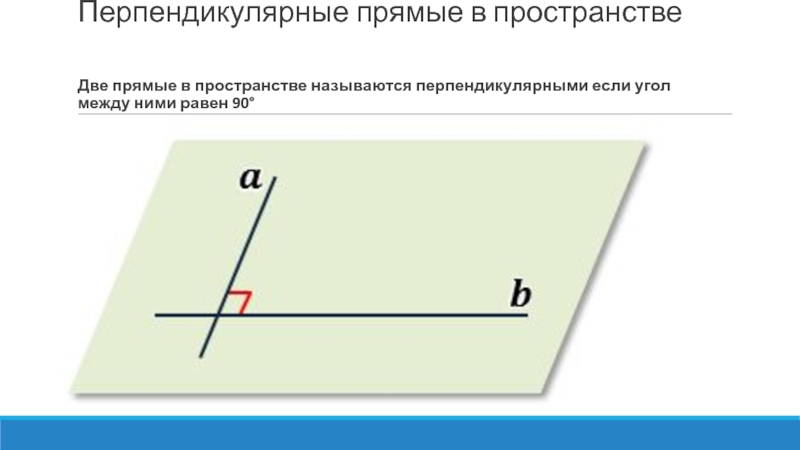
Перпендикулярные прямые в пространстве Две прямые в пространстве называются перпендикулярными если угол между ними равен 90°
Слайд 2Перпендикулярные прямые в пространстве Две прямые в пространстве называются перпендикулярными если угол
между ними равен 90°
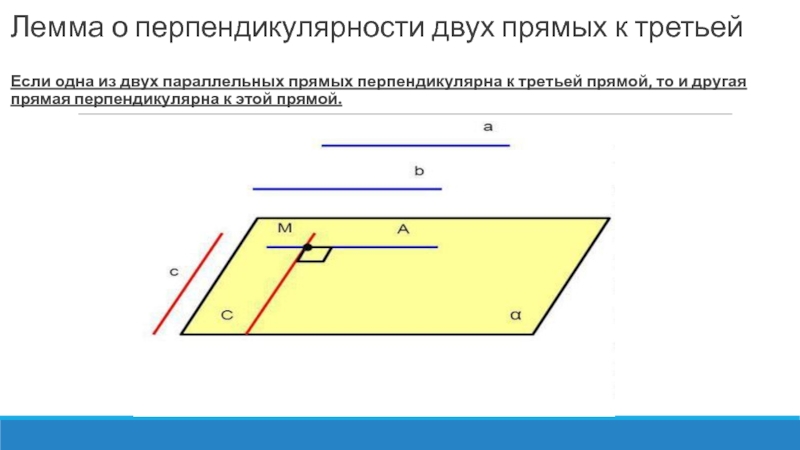
Слайд 3 Лемма о перпендикулярности двух прямых к третьей Если одна из двух параллельных
прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
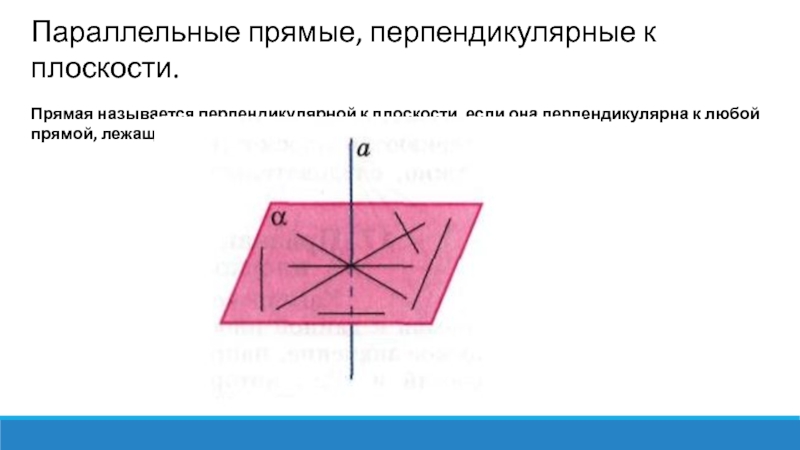
Слайд 4Параллельные прямые, перпендикулярные к плоскости.
Прямая называется перпендикулярной к плоскости, если она
перпендикулярна к любой прямой, лежащей в этой плоскости.
Слайд 5
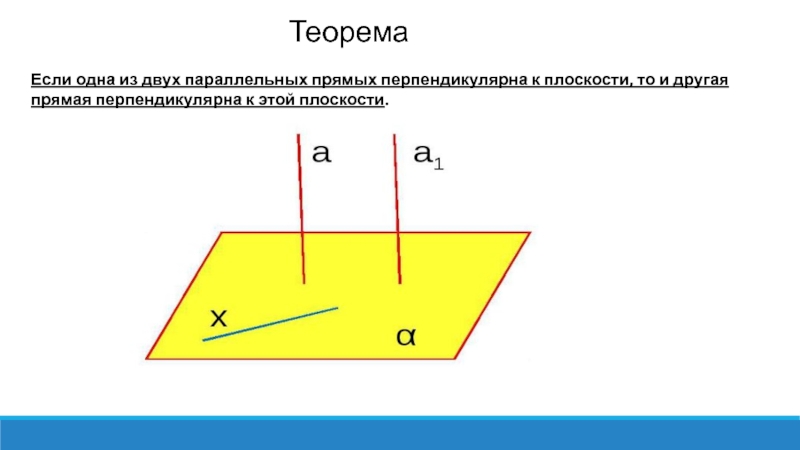
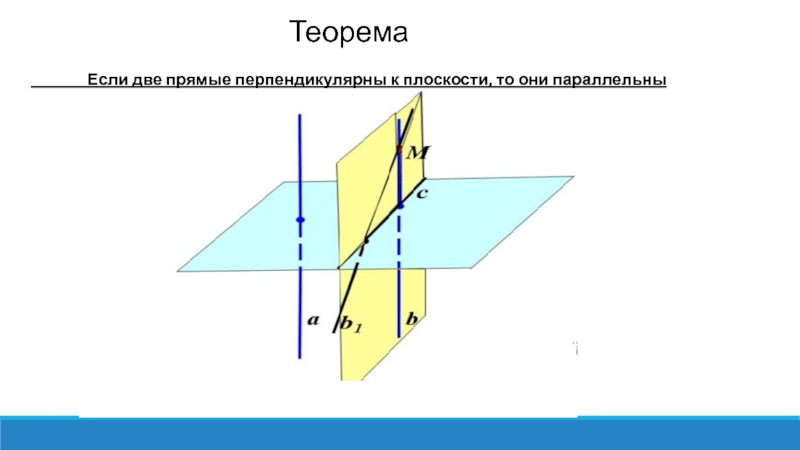
Теорема
Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
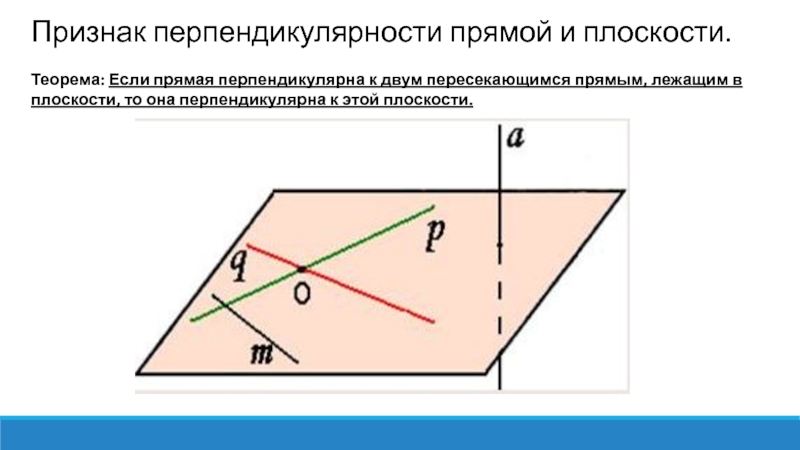
Слайд 7Признак перпендикулярности прямой и плоскости.
Теорема: Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
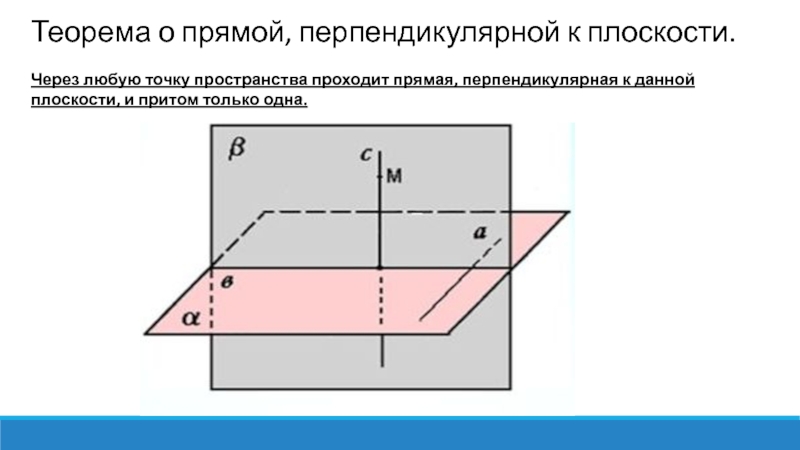
Слайд 8Теорема о прямой, перпендикулярной к плоскости.
Через любую точку пространства
проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
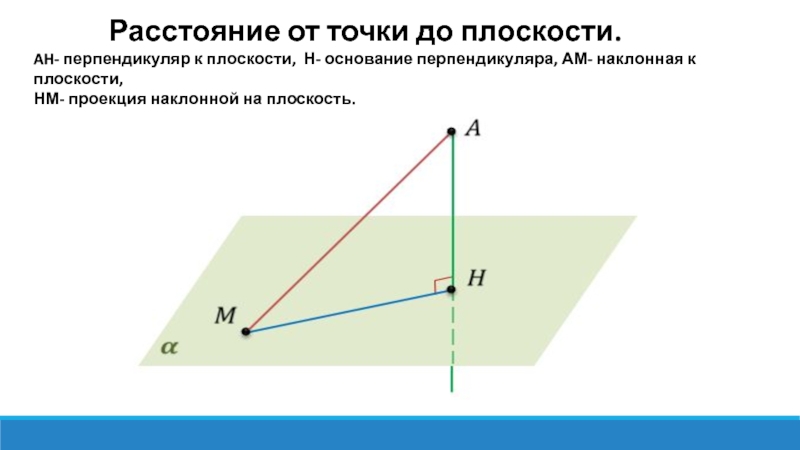
Слайд 10 Расстояние от точки до плоскости.
AH- перпендикуляр к плоскости, Н- основание перпендикуляра, АМ- наклонная к плоскости,
НМ- проекция наклонной на плоскость.
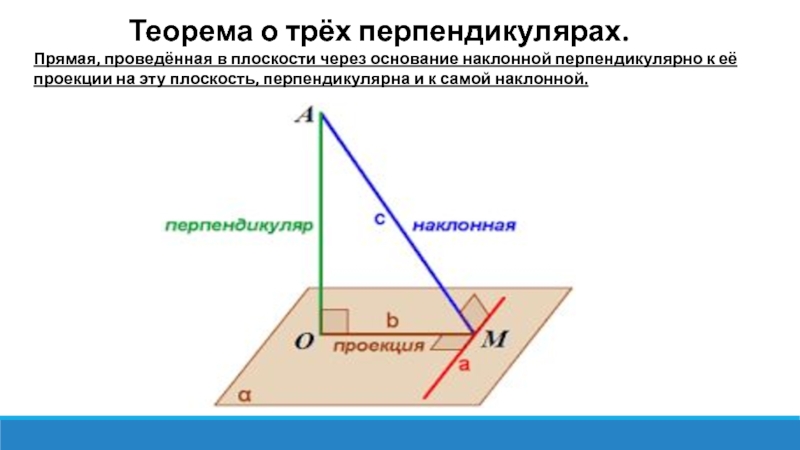
Слайд 11 Теорема о трёх перпендикулярах.
Прямая, проведённая в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна и к самой наклонной.
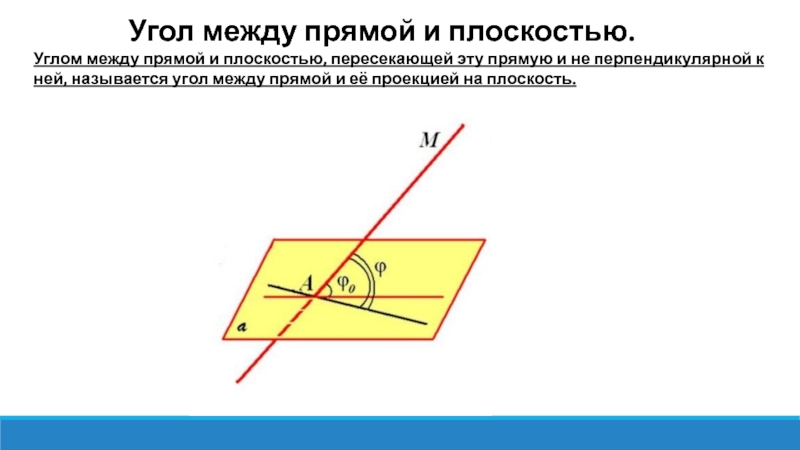
Слайд 12 Угол между прямой и
плоскостью.
Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и её проекцией на плоскость.
Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и её проекцией на плоскость.
Слайд 14
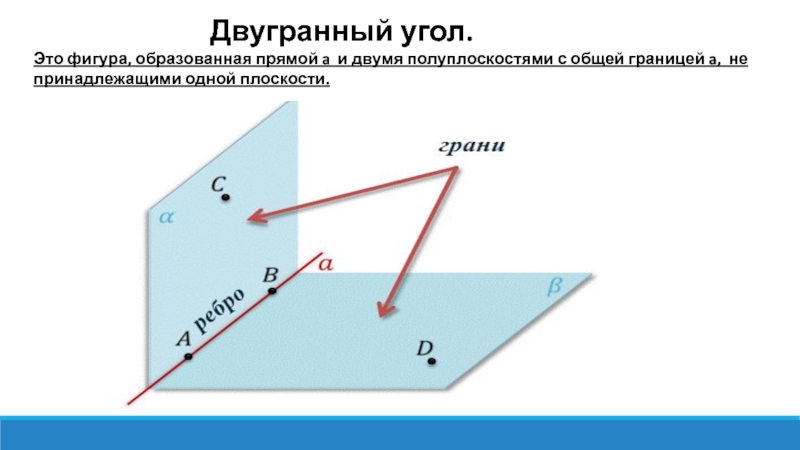
Двугранный угол.
Это фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости.
Это фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости.
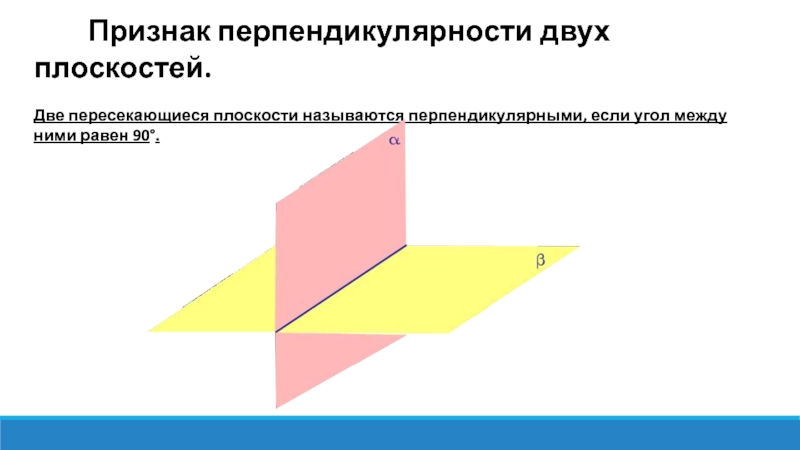
Слайд 16 Признак перпендикулярности двух плоскостей.
Две пересекающиеся
плоскости называются перпендикулярными, если угол между ними равен 90°.
Слайд 17
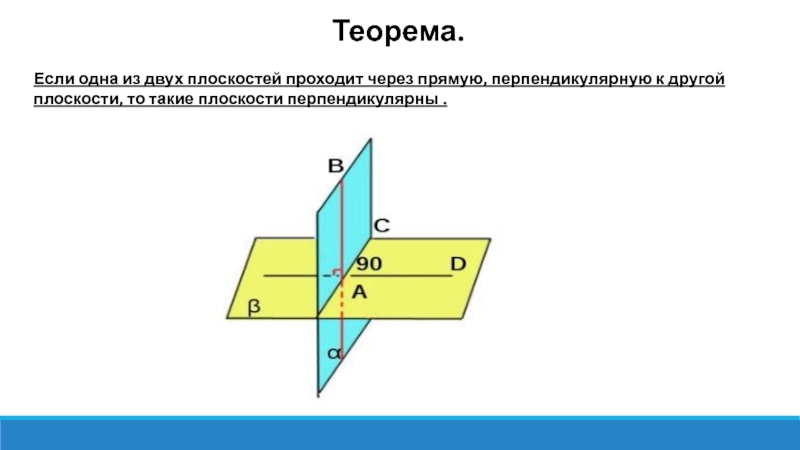
Теорема.
Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны .
Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны .
Слайд 18
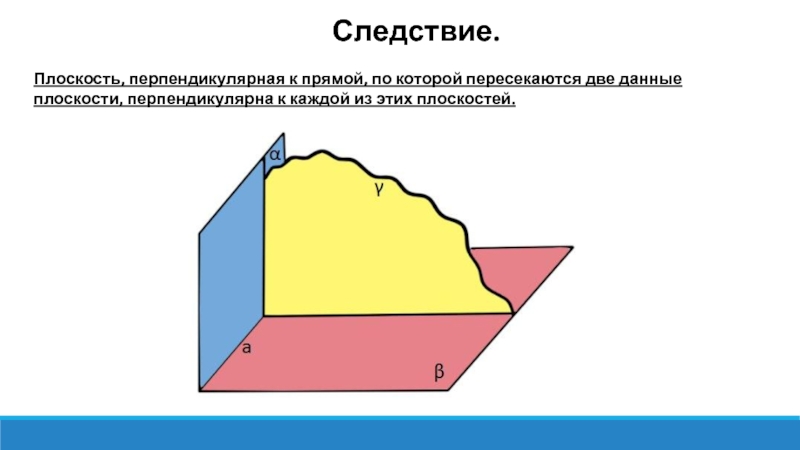
Следствие.
Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.
Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.
Слайд 19
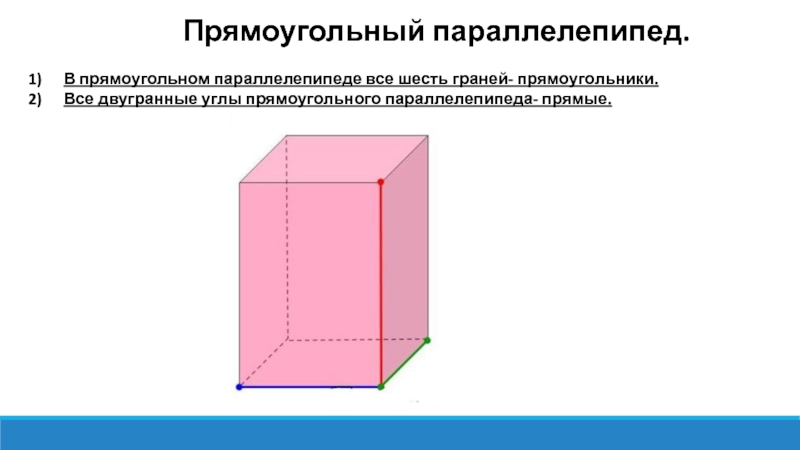
Прямоугольный параллелепипед.
В прямоугольном параллелепипеде все шесть граней- прямоугольники.
Все двугранные углы прямоугольного параллелепипеда- прямые.
В прямоугольном параллелепипеде все шесть граней- прямоугольники.
Все двугранные углы прямоугольного параллелепипеда- прямые.
Слайд 20
Теорема.
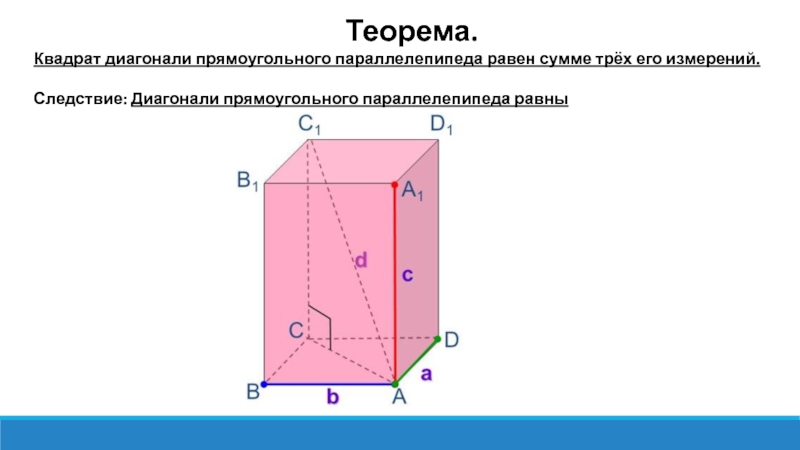
Квадрат диагонали прямоугольного параллелепипеда равен сумме трёх его измерений.
Следствие: Диагонали прямоугольного параллелепипеда равны
Квадрат диагонали прямоугольного параллелепипеда равен сумме трёх его измерений.
Следствие: Диагонали прямоугольного параллелепипеда равны
Слайд 21
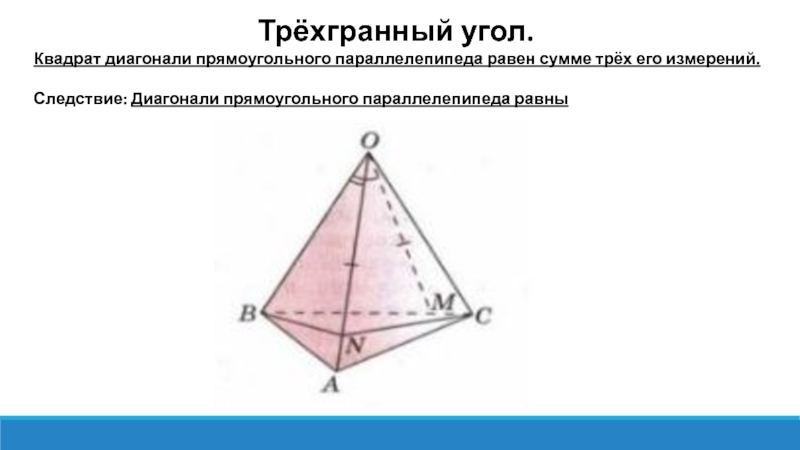
Трёхгранный угол.
Квадрат диагонали прямоугольного параллелепипеда равен сумме трёх его измерений.
Следствие: Диагонали прямоугольного параллелепипеда равны
Квадрат диагонали прямоугольного параллелепипеда равен сумме трёх его измерений.
Следствие: Диагонали прямоугольного параллелепипеда равны