- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Открытый урок по алгебре в 9 классе по теме Целое уравнение и его корни
Содержание
- 1. Открытый урок по алгебре в 9 классе по теме Целое уравнение и его корни
- 2. Цели: образовательные: обобщить и углубить
- 3. Решите уравнения:а) x2 = 0
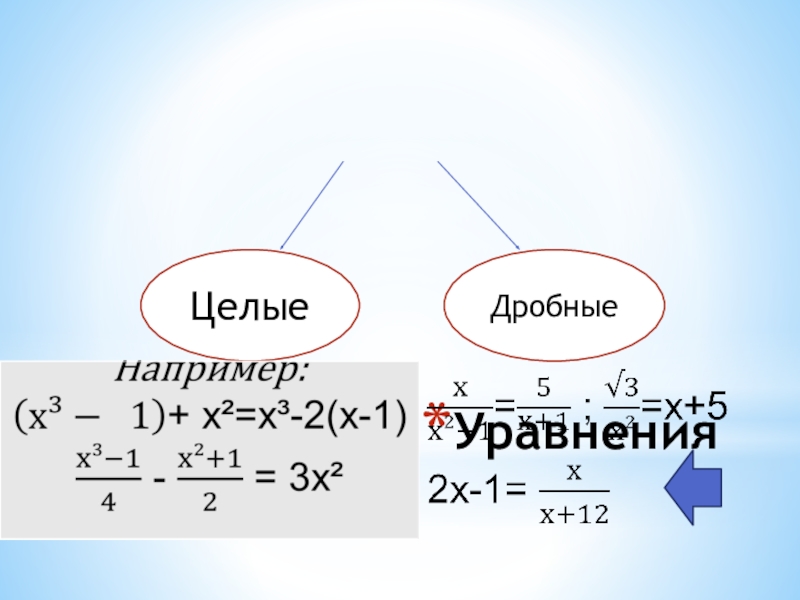
- 4. УравненияЦелыеДробные
- 5. Если уравнение с одной переменной записано
- 6. Какова степень знакомых нам уравнений?а) x2
- 7. Физкультминутка.
- 8. Слайд 8
- 9. Решите уравнения:I вариант
- 10. Решите
- 11. Как вы думаете сколько корней может иметь
- 12. ax + b = 0Линейное уравнениеax²+bx+c=0Квадратное уравнениеМетоды решения целых уравнений:Нет корнейD
- 13. Уравнение третьей степени вида: ax³+bx²+cx+d=0 Путем разложения на множителиРешить уравнение:x³-8x²-x+8=0
- 14. Решить уравнение:(8x-1)(2x-3)-(4x-1)²=38Решение:Раскроем скобки и приведем подобные слагаемые16x²-24x-2x+3-16x²+8x-138=0-18x-36=0x+2=0x=-2Ответ: x=-2
- 15. Спасибо за внимание!
Цели: образовательные: обобщить и углубить сведения об уравнениях;ввести понятие целого уравнения и его степени, его корней;рассмотреть способ решения целого уравнения с помощью разложения на множители.развивающие:развитие математического и общего кругозора, логического мышления, умение анализировать, делать
Слайд 2
Цели:
образовательные:
обобщить и углубить сведения об уравнениях;
ввести понятие целого уравнения
и его степени, его корней;
рассмотреть способ решения целого уравнения с помощью разложения на множители.
развивающие:
развитие математического и общего кругозора, логического мышления, умение анализировать, делать вывод;
воспитательные:
воспитывать самостоятельность, четкость и аккуратность в действиях.
рассмотреть способ решения целого уравнения с помощью разложения на множители.
развивающие:
развитие математического и общего кругозора, логического мышления, умение анализировать, делать вывод;
воспитательные:
воспитывать самостоятельность, четкость и аккуратность в действиях.
Слайд 3Решите уравнения:
а) x2 = 0
е) x3 – 25x = 0
б) 3x – 5 = 0 ж) x(x – 1)(x + 2) = 0
в) x2 –5 = 0 з) x4 – x2 = 0
г) x2 = 1/36 и) x2 –0,01 = 0,03
д) x2 = – 25 к) 19 – c2 = 10
Слайд 5 Если уравнение с одной переменной
записано в виде
P(x) =
0, где P(x)- многочлен стандартного вида,
то степень этого многочлена называют
степенью данного уравнения
то степень этого многочлена называют
степенью данного уравнения
Например:
Слайд 6Какова степень знакомых
нам уравнений?
а) x2 = 0
е) x3 – 25x = 0
б) 3x – 5 = 0 ж) x(x – 1)(x + 2) = 0
в) x2 – 5 = 0 з) x4 – x2 = 0
г) x2 = 1/36 и) x2 – 0,01 = 0,03
д) x2 = – 25 к) 19 – c2 = 10
б) 3x – 5 = 0 ж) x(x – 1)(x + 2) = 0
в) x2 – 5 = 0 з) x4 – x2 = 0
г) x2 = 1/36 и) x2 – 0,01 = 0,03
д) x2 = – 25 к) 19 – c2 = 10
Слайд 8
Решите уравнения:
2∙х + 5 =15
0∙х = 7
Сколько корней может иметь уравнение
I степени?
Не более одного!
Не более одного!
Слайд 9
Решите уравнения:
I вариант II вариант III
вариант
x2-5x+6=0 y2-4y+7=0 x2-12x+36=0
D=1, D>0, D=-12, D<0 D=0,1 корень
x1=2, x2=3 нет корней x=6.
Сколько корней может иметь уравнение I I степени (квадратное)?
Не более двух!
x2-5x+6=0 y2-4y+7=0 x2-12x+36=0
D=1, D>0, D=-12, D<0 D=0,1 корень
x1=2, x2=3 нет корней x=6.
Сколько корней может иметь уравнение I I степени (квадратное)?
Не более двух!
Слайд 10
Решите уравнения:
I вариант II вариант
III вариант
x3-1=0 x3- 4x=0 x3-12x2+36x=0
x3=1 x(x2- 4)=0 x(x2-12x+36)=0
x=1 x=0, x=2, x= -2 x=0, x=6
1 корень 3 корня 2 корня
Сколько корней может иметь уравнение I I I степени?
Не более трех!
x3-1=0 x3- 4x=0 x3-12x2+36x=0
x3=1 x(x2- 4)=0 x(x2-12x+36)=0
x=1 x=0, x=2, x= -2 x=0, x=6
1 корень 3 корня 2 корня
Сколько корней может иметь уравнение I I I степени?
Не более трех!
Слайд 11Как вы думаете сколько корней может иметь уравнение
IV,
V , VI, VII, n-й степени?
Не более четырёх, пяти, шести, семи корней!
Вообще не более n корней !
Не более четырёх, пяти, шести, семи корней!
Вообще не более n корней !
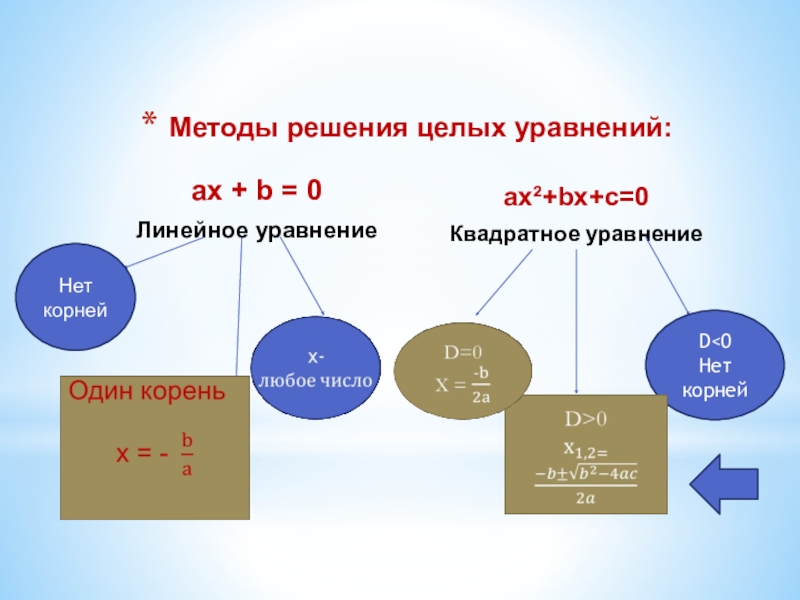
Слайд 12ax + b = 0
Линейное уравнение
ax²+bx+c=0
Квадратное уравнение
Методы решения целых уравнений:
Нет корней
D
корней