- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Основы комбинаторики
Содержание
- 1. Основы комбинаторики
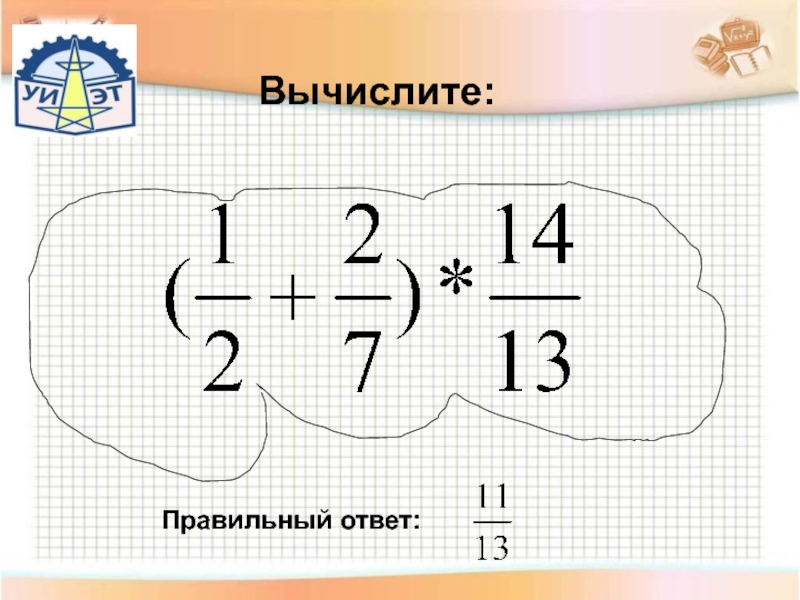
- 2. Вычислите:Правильный ответ:
- 3. Вычислите:Правильный ответ:60
- 4. ВЫЧИСЛИТЕ:2! = 3! = 5! = 26120При решении каких задач применяется факториал?
- 5. ВЫЧИСЛИТЕ:2524
- 6. Элементы комбинаторики
- 7. Комбинаторика Комбинаторика – это раздел математики, в
- 8. ИСТОРИЧЕСКАЯ СПРАВКА Термин "комбинаторика" был
- 9. Комбинаторика занимается различного рода соединениями (перестановки, размещения, сочетания), которые можно образовать из элементов некоторого конечного множества.
- 10. Комбинаторные соединенияПерестановкиПерестановки без повторенийПерестановки с повторениямиРазмещенияРазмещения без повторенийРазмещения с повторениямиСочетанияСочетания без повторенийСочетания с повторениями
- 11. Перестановки – соединения, которые можно
- 12. Перестановки с повторениями Всякое размещение с повторениями, в
- 13. Размещения Размещением из n элементов по k (
- 14. Размещения с повторениямиРазмещения с повторениями – соединения,
- 15. Сочетания Сочетания – соединения, содержащие по m предметов
- 16. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 17. Пример Сколькими способами
- 18. Проверь себя1) Сколькими способами можно поставить рядом на полке четыре различные книги?
- 19. Проверь себя 1) Сколькими способами можно
- 20. Проверь себя 2) Сколькими способами можно
- 21. Проверь себя 2) Сколькими способами можно
- 22. Проверь себя3) Сколькими способами можно рассадить восьмерых детей на восьми стульях в столовой детского сада?
- 23. Проверь себя3) Сколькими способами можно рассадить восьмерых
- 24. Проверь себя4) Сколько различных слов можно составить,
- 25. Проверь себя4) Сколько различных слов можно составить,
- 26. Проверь себя5) Сколькими способами можно установить дежурство
- 27. Проверь себя5) Сколькими способами можно установить дежурство
- 28. Пример Слова и фразы с переставленными буквами называют
- 29. Проверь себя1) Сколько различных слов можно получить, переставляя буквы слова "математика" ?
- 30. Проверь себя1) Сколько различных слов можно получить,
- 31. Проверь себя2) Сколькими способами можно расставить на
- 32. Проверь себя2) Сколькими способами можно расставить на
- 33. Проверь себя3) У мамы 2 яблока, 3
- 34. Проверь себя3) У мамы два яблока, три
- 35. Историческая справка Комбинаторные мотивы можно заметить еще в
- 36. Пример Сколькими способами из 40 учеников класса можно
- 37. Проверь себя1. Из семи различных книг выбирают четыре. Сколькими способами это можно сделать?
- 38. Проверь себяИз семи различных книг выбирают четыре. Сколькими способами это можно сделать? Решение.
- 39. Проверь себя2. В чемпионате по футболу участвуют
- 40. Проверь себя2. В чемпионате по футболу участвуют
- 41. Проверь себя3. В классе изучаются 7 предметов.
- 42. Проверь себяВ классе изучаются 7 предметов. В
- 43. Пример использования В библиотеку, в которой есть много
- 44. Решение задачи Так как учебники по каждому предмету
- 45. Проверь себя!1. Телефонный номер состоит из 7
- 46. Проверь себя!1. Телефонный номер состоит из 7
- 47. Проверь себя!2. Сколькими способами можно написать слово, составленное из четырех букв английского алфавита?РЕШЕНИЕ
- 48. Проверь себя!2. Сколькими способами можно написать слово,
- 49. Проверь себя!3. В магазине, где есть 4
- 50. Проверь себя!3. В магазине, где есть 4
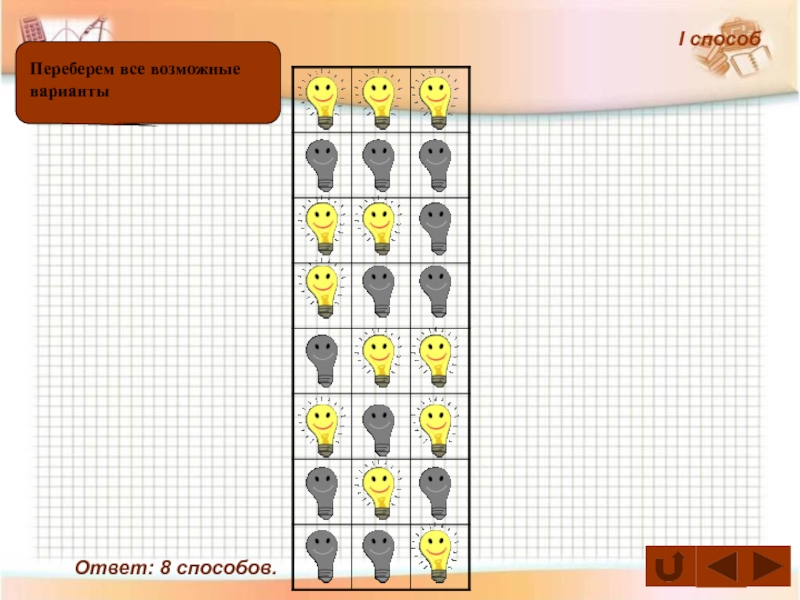
- 51. В коридоре висят три лампочки. Сколько имеется различных способов освещения коридора?Задача 5
- 52. Ответ: 8 способов.Переберем все возможные вариантыІ способ
- 53. Воспользуемся правилом умноженияДля каждой лампочки возможны два исхода, а лампочек три, значит:Ответ:8.ІІ способ
- 54. Выберите правило№1. Из города А а город
- 55. Решите задачи
- 56. Домашнее задание
- 57. Используемая литератураАлгебра и начала математического анализа.11 класс/
Вычислите:Правильный ответ:
Слайд 7Комбинаторика
Комбинаторика – это раздел
математики, в котором изучаются
вопросы
выбора или расположения
элементов множества в соответствии
с заданными правилами.
«Комбинаторика» происходит от латинского
слова «combina», что в переводе на русский
означает – «сочетать», «соединять».
элементов множества в соответствии
с заданными правилами.
«Комбинаторика» происходит от латинского
слова «combina», что в переводе на русский
означает – «сочетать», «соединять».
Слайд 8
ИСТОРИЧЕСКАЯ СПРАВКА
Термин "комбинаторика" был введён в математический обиход
всемирно известным немецким учёным Г.В.Лейбницем, который в 1666 году опубликовал "Рассуждения о комбинаторном искусстве".
В XVIII веке к решению комбинаторных задач обращались и другие выдающиеся математики. Так, Леонард Эйлер рассматривал задачи о разбиении чисел, о паросочетаниях, о циклических расстановках, о построении магических и латинских квадратов.
Г.В.Лейбниц
Слайд 9 Комбинаторика занимается различного рода соединениями (перестановки, размещения, сочетания), которые можно образовать
из элементов некоторого конечного множества.
Слайд 10Комбинаторные соединения
Перестановки
Перестановки без повторений
Перестановки с повторениями
Размещения
Размещения без повторений
Размещения с повторениями
Сочетания
Сочетания без
повторений
Сочетания с повторениями
Сочетания с повторениями
Слайд 11 Перестановки – соединения, которые можно составить из n элементов,
меняя всеми возможными способами их порядок.
Формула:
Слайд 12Перестановки с повторениями
Всякое размещение с повторениями, в котором элемент а1 повторяется
k1 раз, элемент a2 повторяется k2 раз и т.д. элемент an повторяется kn раз, где k1, k2, ..., kn — данные числа, называется перестановкой с повторениями порядка
n = k1 + k2 + … + kn, в которой данные элементы a1, a2, …, an повторяются соответственно k1, k2, .., kn раз.
n = k1 + k2 + … + kn, в которой данные элементы a1, a2, …, an повторяются соответственно k1, k2, .., kn раз.
Слайд 13Размещения
Размещением из n элементов по k
( ) называется любое
множество, состоящее из любых k элементов, взятых в определенном порядке из n элементов.
Два размещения из n элементов считаются различными, если они отличаются самими элементами или порядком их расположения.
Два размещения из n элементов считаются различными, если они отличаются самими элементами или порядком их расположения.
Слайд 14Размещения с повторениями
Размещения с повторениями – соединения, содержащие n элементов, выбираемых
из элементов m различных видов ( ) и отличающиеся одно от другого либо составом, либо порядком элементов.
Слайд 15Сочетания
Сочетания – соединения, содержащие по m предметов из n, различающихся друг
от друга по крайней мере одним предметом.
Сочетания – конечные множества, в которых порядок не имеет значения.
Слайд 17Пример
Сколькими способами могут 8 человек встать
в очередь к театральной кассе?
Ответ: P8 = 8!=40320
Слайд 19Проверь себя
1) Сколькими способами можно поставить рядом на полке
четыре различные книги?
Ответ: 24 способа
Решение.
На первое место можно поставить одну из четырех книг, на вторую – любую из трех, на третье – любую из двух и на четвертое – последнюю оставшуюся книгу. Применяя последовательно правило произведения, получим Р(4) = 4х3х2х1=24.
Слайд 20Проверь себя
2) Сколькими способами можно положить 10 различных открыток
в 10 имеющихся конвертов (по одной открытке в конверт)?
Слайд 21Проверь себя
2) Сколькими способами можно положить 10 различных открыток
в 10 имеющихся конвертов (по одной открытке в конверт)?
Ответ: 3628800 способа
Решение.
По формуле перестановки находим:
Р(10)= 10! =1х2х3х…х9х10=3628800
Слайд 22Проверь себя
3) Сколькими способами можно рассадить восьмерых детей на восьми стульях
в столовой детского сада?
Слайд 23Проверь себя
3) Сколькими способами можно рассадить восьмерых детей на восьми стульях
в столовой детского сада?
Ответ: 40320 способа
Решение.
По формуле перестановки находим:
Р(8)= 8! =1х2х3х…х7х8=40320
Слайд 24Проверь себя
4) Сколько различных слов можно составить, переставляя местами буквы в
слове «треугольник» (считая и само это слово)?
Слайд 25Проверь себя
4) Сколько различных слов можно составить, переставляя местами буквы в
слове «треугольник» (считая и само это слово)?
Ответ: 39916800 слов.
Решение.
По формуле перестановки находим:
Р(11)= 11! = 1х2х3х…х10х11= 39916800
Слайд 26Проверь себя
5) Сколькими способами можно установить дежурство по одному человеку в
день среди семи учащихся группы в течение 7 дней (каждый должен отдежурить один раз)?
Слайд 27Проверь себя
5) Сколькими способами можно установить дежурство по одному человеку в
день среди семи учащихся группы в течение 7 дней (каждый должен отдежурить один раз)?
Ответ: 5040 способа.
Решение.
По формуле перестановки находим:
Р(7)= 7! = 1х2х3х…х6х7= 5040
Слайд 28Пример
Слова и фразы с переставленными буквами называют анаграммами.
Сколько анаграмм можно
составить из слова «макака»?
Решение.
Решение.
Всего в слове «МАКАКА» 6 букв (m=6).
Определим сколько раз в слове используется каждая буква:
«М» - 1 раз (k1=1)
«А» - 3 раза (k2=3)
«К» - 2 раза (k3=2)
Р =
m!
k1! k2! …kn!
Р1,3,2 =
6!
1! 3! 2!
=
4*5*6
2
=
60.
Слайд 29Проверь себя
1) Сколько различных слов можно получить, переставляя буквы слова "математика"
?
Слайд 30Проверь себя
1) Сколько различных слов можно получить, переставляя буквы слова "математика"
?
Решение.
Всего в слове «МАТЕМАТИКА» 10 букв (m=10).
Определим, сколько раз в слове используется каждая буква: «М» - 2; «А» - 3; «Т» - 2; «Е» - 1; «И» - 1; «К» -1. (k1, k2, … , kn)
Слайд 31Проверь себя
2) Сколькими способами можно расставить на первой горизонтали шахматной доски
комплект белых фигур (король, ферзь, две ладьи, два слона и два коня)?
Слайд 32Проверь себя
2) Сколькими способами можно расставить на первой горизонтали шахматной доски
комплект белых фигур (король, ферзь, две ладьи, два слона и два коня)?
Решение.
Комплект белых шахматных фигур состоит из 8 фигур:
1 король, 1 ферзь, 2 ладьи, 2 слона и 2 коня
(m=8; k1, k2, … , kn)
Слайд 33Проверь себя
3) У мамы 2 яблока, 3 груши и 4 апельсина.
Каждый день в течение девяти дней подряд она дает сыну один из оставшихся фруктов. Сколькими способами это может быть сделано?
Слайд 34Проверь себя
3) У мамы два яблока, три груши и четыре апельсина.
Каждый день в течение девяти дней подряд она дает сыну один из оставшихся фруктов. Сколькими способами это может быть сделано?
Решение.
У мамы всего 9 фруктов: два яблока, три груши и четыре апельсина. (k1, k2, … , kn)
Слайд 35Историческая справка
Комбинаторные мотивы можно заметить еще в символике китайской «Книги перемен» (V
век до н. э.).
В XII в. индийский математик Бхаскара в своём основном труде «Лилавати» подробно исследовал задачи с перестановками и сочетаниями, включая перестановки с повторениями.
В XII в. индийский математик Бхаскара в своём основном труде «Лилавати» подробно исследовал задачи с перестановками и сочетаниями, включая перестановки с повторениями.
Слайд 36Пример
Сколькими способами из 40 учеников класса можно выделить актив в следующем
составе: староста, физорг и редактор стенгазеты?
Решение:
Требуется выделить упорядоченные трехэлементные подмножества множества, содержащего 40 элементов, т.е. найти число размещений без повторений из 40 элементов по 3.
Решение:
Требуется выделить упорядоченные трехэлементные подмножества множества, содержащего 40 элементов, т.е. найти число размещений без повторений из 40 элементов по 3.
Слайд 37Проверь себя
1. Из семи различных книг выбирают четыре. Сколькими способами это
можно сделать?
Слайд 38Проверь себя
Из семи различных книг выбирают четыре. Сколькими способами это можно
сделать?
Решение.
Решение.
Слайд 39Проверь себя
2. В чемпионате по футболу участвуют десять команд. Сколько существует
различных возможностей занять командам первые три места?
Слайд 40Проверь себя
2. В чемпионате по футболу участвуют десять команд. Сколько существует
различных возможностей занять командам первые три места?
Решение.
Решение.
А = =720
Слайд 41Проверь себя
3. В классе изучаются 7 предметов. В среду 4
урока, причем все разные. Сколькими способами можно составить расписание на среду?
Слайд 42Проверь себя
В классе изучаются 7 предметов. В среду 4 урока,
причем все разные. Сколькими способами можно составить расписание на среду?
Решение.
Решение.
Слайд 43Пример использования
В библиотеку, в которой есть много одинаковых учебников по десяти
предметам, пришло 5 школьников, каждый из которых хочет взять учебник. Библиотекарь записывает в журнал по порядку названия (без номера) взятых учебников без имен учеников, которые их взяли. Сколько разных списков в журнале могло появиться?
Слайд 44Решение задачи
Так как учебники по каждому предмету одинаковые, и библиотекарь записывает
лишь название (без номера),то список – размещение с повторением, число элементов исходного множества равно 10, а количество позиций – 5.
Тогда количество разных списков равно
= 100000.
Ответ: 100000
Тогда количество разных списков равно
= 100000.
Ответ: 100000
Слайд 45Проверь себя!
1. Телефонный номер состоит из 7 цифр. Какое наибольшее число
звонков неудачник-Петя может совершить прежде, чем угадает правильный номер.
РЕШЕНИЕ
РЕШЕНИЕ
Слайд 46Проверь себя!
1. Телефонный номер состоит из 7 цифр. Какое наибольшее число
звонков неудачник-Петя может совершить прежде, чем угадает правильный номер.
Решение.
Т.к. цифры могут повторяться, то всего возможно
разных номеров.
Если Петя невезучий, он должен будет звонить 10 миллионов раз.
Ответ: 10000000.
Решение.
Т.к. цифры могут повторяться, то всего возможно
разных номеров.
Если Петя невезучий, он должен будет звонить 10 миллионов раз.
Ответ: 10000000.
Слайд 47Проверь себя!
2. Сколькими способами можно написать слово, составленное из четырех букв
английского алфавита?
РЕШЕНИЕ
Слайд 48Проверь себя!
2. Сколькими способами можно написать слово, составленное из четырех букв
английского алфавита?
Решение.
В английском алфавите 26 букв, буквы могут повторяться, значит, количество слов равно
(26 элементов и 4 позиции)
Ответ:
Решение.
В английском алфавите 26 букв, буквы могут повторяться, значит, количество слов равно
(26 элементов и 4 позиции)
Ответ:
Слайд 49Проверь себя!
3. В магазине, где есть 4 вида мячей, решили поставить
в ряд 8 мячей. Сколькими способами можно это сделать, если их расположение имеет значение?
Слайд 50Проверь себя!
3. В магазине, где есть 4 вида мячей, решили поставить
в ряд 8 мячей. Сколькими способами можно это сделать, если их расположение имеет значение?
Решение.
Разных видов мячей 4, позиций 8, т.е. количество различных размещений будет равно = 65536.
Ответ: 65536 способов.
Решение.
Разных видов мячей 4, позиций 8, т.е. количество различных размещений будет равно = 65536.
Ответ: 65536 способов.
Слайд 51В коридоре висят три лампочки. Сколько имеется различных способов освещения коридора?
Задача
5
Слайд 53
Воспользуемся правилом умножения
Для каждой лампочки возможны два исхода, а лампочек три,
значит:
Ответ:8.
ІІ способ
Слайд 54Выберите правило
№1. Из города А а город В ведут 5 дорог,
а из города В в город С – 3 дороги. Сколькими способами можно проехать из города А в город С?
№2. На книжной полке стоят 3 книги по алгебре, 4 по геометрии и 5 по литературе. Сколькими способами можно взять с полки одну книгу по математике?
№3. В меню имеется 4 первых блюда, 3 – вторых, 2 – десерта. Сколько различных обедов можно из них составить?
№2. На книжной полке стоят 3 книги по алгебре, 4 по геометрии и 5 по литературе. Сколькими способами можно взять с полки одну книгу по математике?
№3. В меню имеется 4 первых блюда, 3 – вторых, 2 – десерта. Сколько различных обедов можно из них составить?
Слайд 57Используемая литература
Алгебра и начала математического анализа.11 класс/ Ю.М.Колягин, М.В.Ткачева, Н.Е.Федорова, М.И.Шабунин.
– М.:Просвещение, 2011.
Виленкин Н.Я. Комбинаторика. – М., 1969
Виленкин Н.Я. Комбинаторика. – МЦМНО, 2010
ru.wikipedia.org›wiki/История комбинаторики
Виленкин Н.Я. Комбинаторика. – М., 1969
Виленкин Н.Я. Комбинаторика. – МЦМНО, 2010
ru.wikipedia.org›wiki/История комбинаторики
