каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение.
В. Произволов.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Многогранники. Виды задач и методы их решений
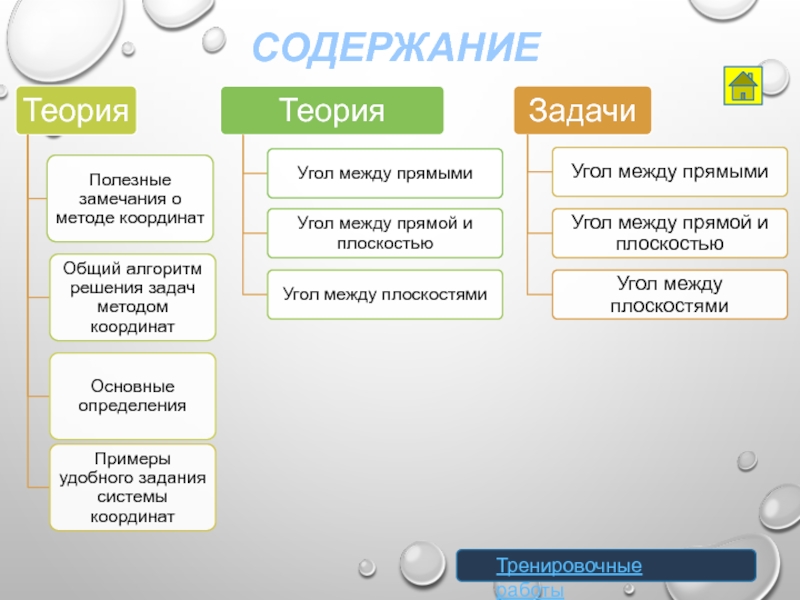
Содержание
- 1. Многогранники. Виды задач и методы их решений
- 2. СодержаниеТренировочные работы
- 3. Слайд 3
- 4. Полезные замечания:Любую задачу №14 можно решить методом
- 5. Общий алгоритм для решения №14 методом координат
- 6. Основные определенияОпределение 1. Ненулевой вектор называется направляющим
- 7. Определение 4. Угол между прямой и плоскостью
- 8. Определение 6. Отрезок, имеющий концы на двух
- 9. Примеры «удобного» задания системы координат для разных объектов Прямоугольный параллелепипедхyz
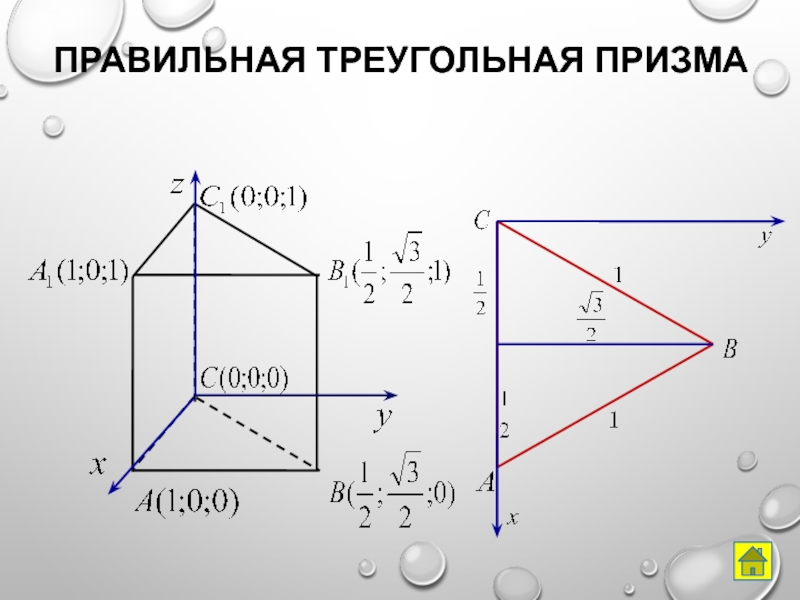
- 10. Правильная треугольная призма
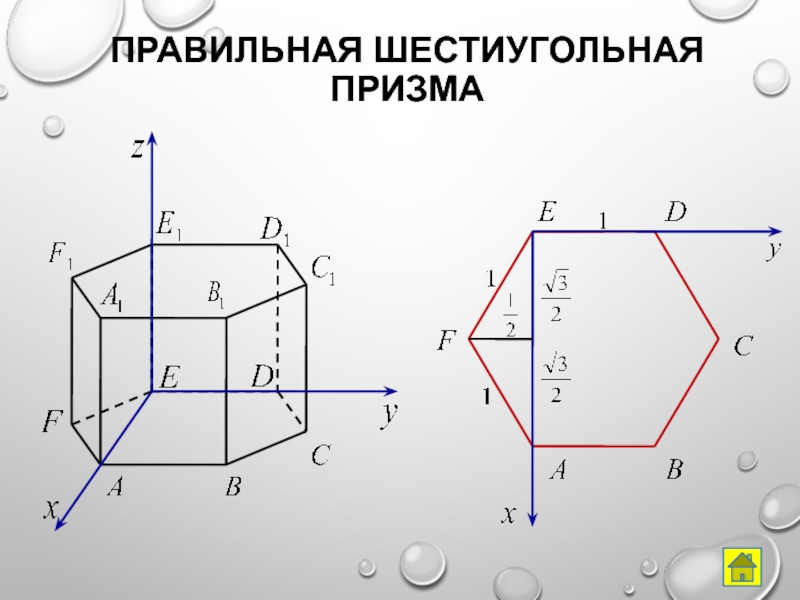
- 11. Правильная шестиугольная призма
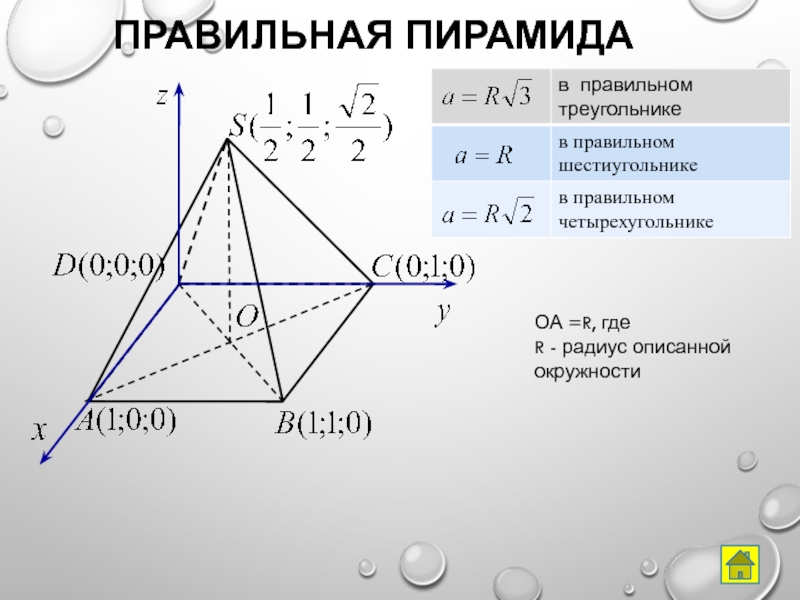
- 12. Правильная пирамидаОА =R, где R - радиус описанной окружности
- 13. Углом между двумя пересекающимися прямыми называется наименьший
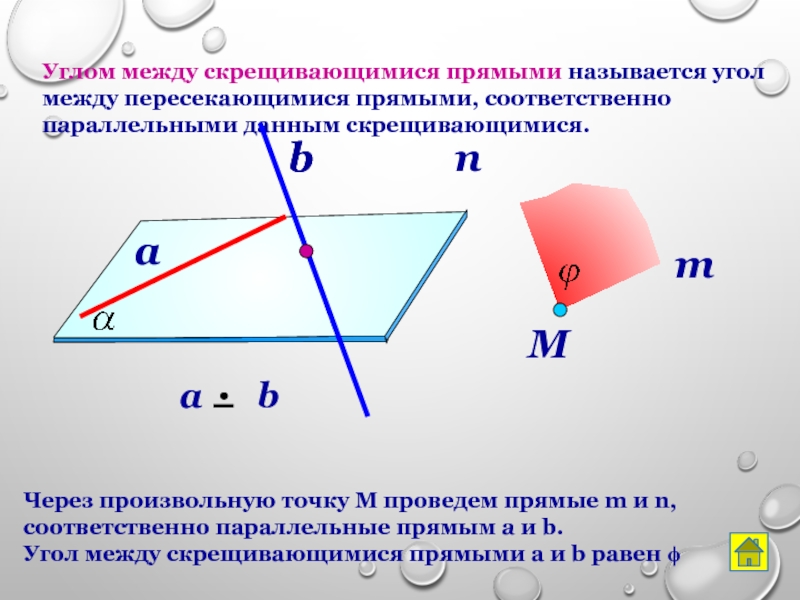
- 14. Углом между скрещивающимися прямыми называется угол между
- 15. Углом между скрещивающимися прямыми называется угол между
- 16. Угол между прямыми
- 17. Угол между прямыми (обозначим α)Используем формулу:Где {x1;y1;z1}
- 18. Угол между прямой и плоскостьюаа1φ0сφHMOОпределение. Угол
- 19. Как построить угол между прямой а и
- 20. Угол между прямой и плоскостьюα -
- 21. Угол между прямой и плоскостью Скалярное произведениеДлины векторов
- 22. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
- 23. Уравнение плоскостиЕсли плоскость проходит через начало координат,
- 24. Двугранный угол, образованный полуплоскостями измеряется величиной его
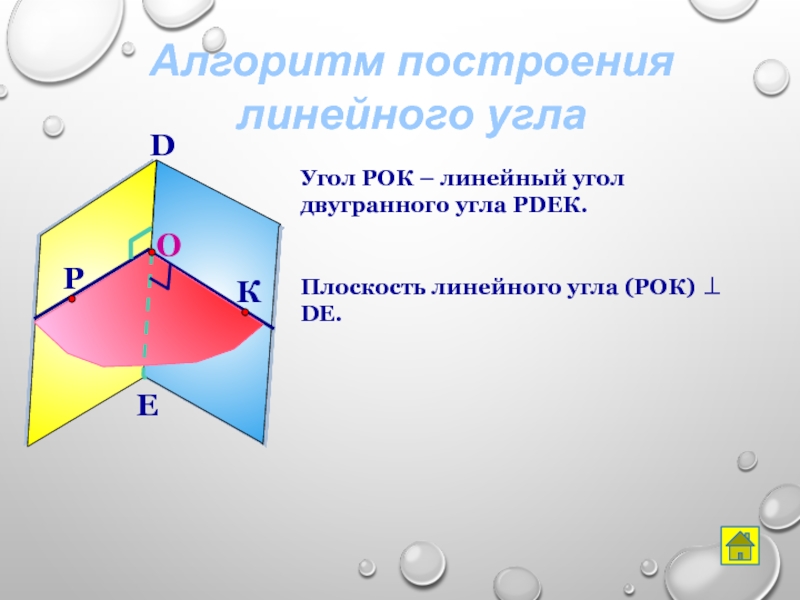
- 25. Алгоритм построения линейного углаDEУгол РОК – линейный угол двугранного угла РDEК.Плоскость линейного угла (РОК) DE.
- 26. 1) Как угол между прямыми, лежащими в
- 27. Угол между плоскостямиУгол между плоскостями равен углу между перпендикулярами к этим плоскостям
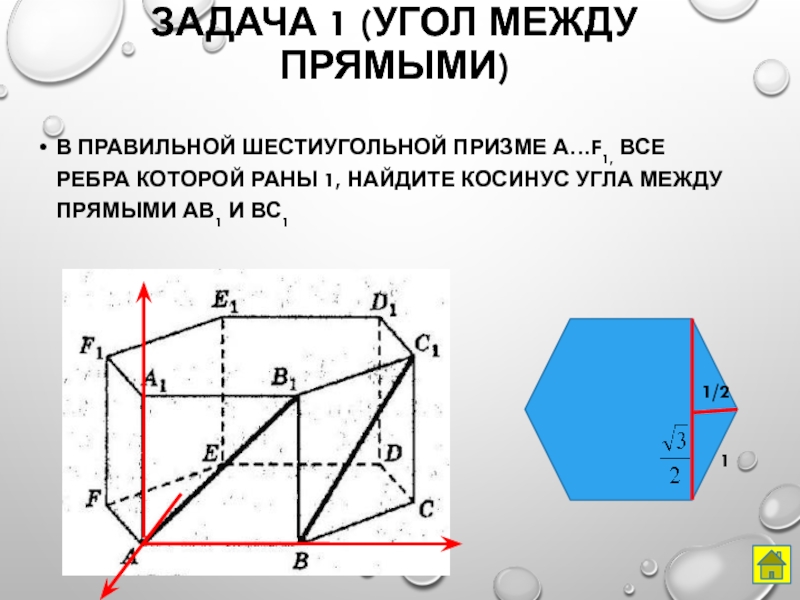
- 28. Задача 1 (угол между прямыми)В правильной шестиугольной
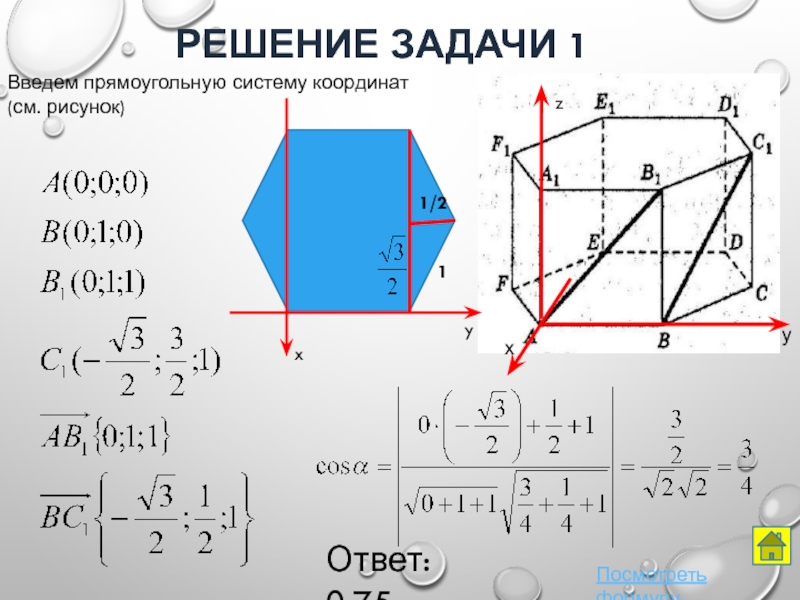
- 29. Решение задачи 111/2Ответ: 0,75Введем прямоугольную систему координат (см. рисунок)xyПосмотреть формулу
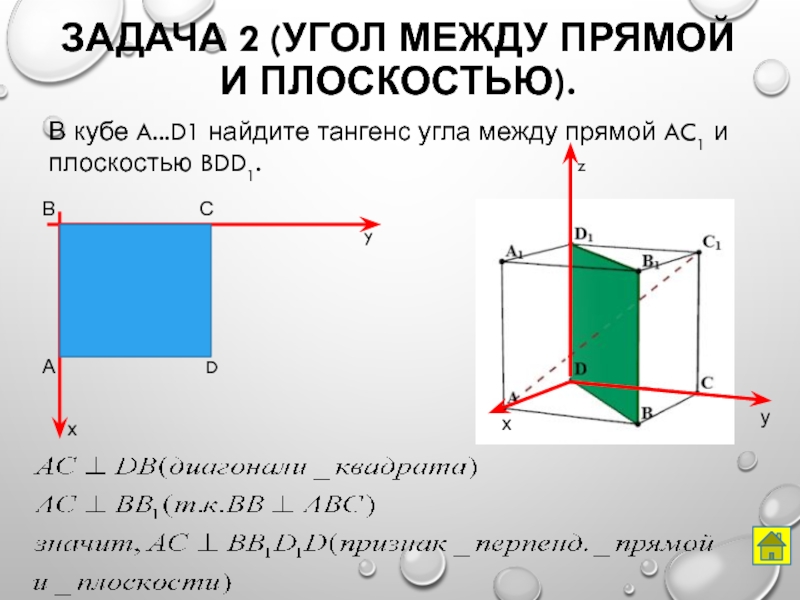
- 30. В кубе A...D1 найдите тангенс угла между
- 31. Введем прямоугольную систему координат (см. рисунок)АDСВА(1;0;0)С(0;1;0)С1(0;1;1)Пусть α – искомый угол)Посмотреть формулуРешение задачи 2
- 32. Задача 3.Угол между плоскостямиВ правильной четырехугольной пирамиде
- 33. Решение задачи 3(1) aх+by+cz+d=0 – общий вид
- 34. Решение задачи 3(продолжение)Аналогично найдем координатыВектора, перпендикулярногоплоскости SCD
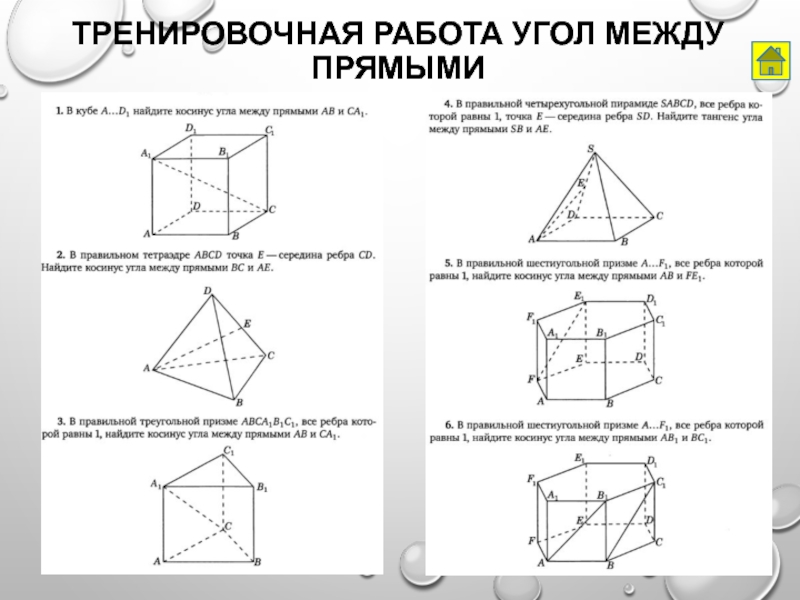
- 35. Тренировочная работа Угол между прямыми
- 36. Тренировочная работа Угол между прямой и плоскостью
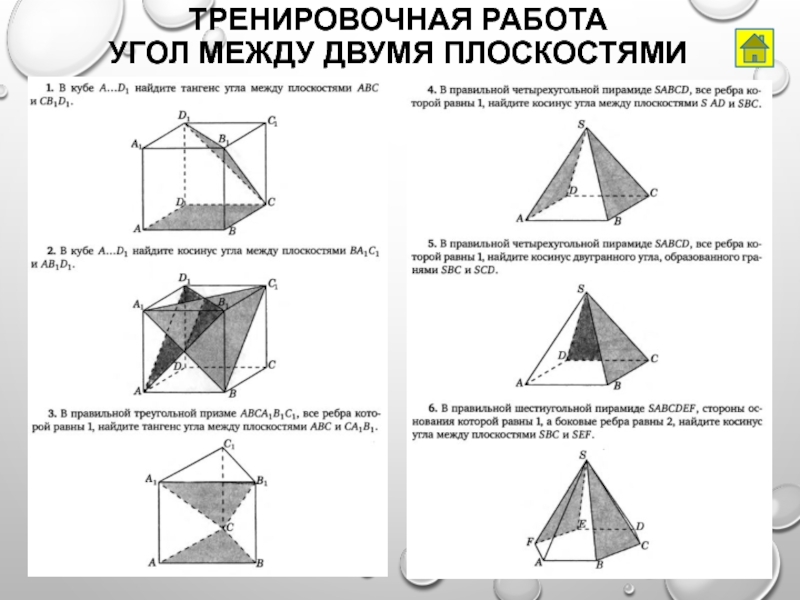
- 37. Тренировочная работа Угол между двумя плоскостями
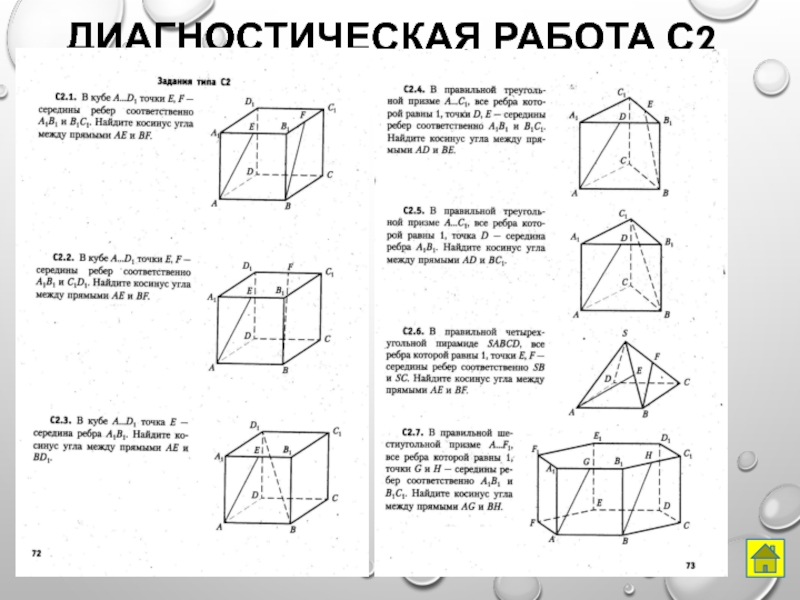
- 38. Диагностическая работа С2
- 39. Слайд 39
- 40. Слайд 40
- 41. Ответы к диагностической работе
СодержаниеТренировочные работы
Слайд 4Полезные замечания:
Любую задачу №14 можно решить методом координат.
Метод координат – не
единственный метод решения задач №14.
Метод координат универсален, потому что есть алгоритм решения для любого типа заданий №14.
Целесообразно задавать систему координат специальным способом для разных объектов.
Целесообразно изображать плоскость Оху и основание геометрического тела в ней отдельно.
Метод координат универсален, потому что есть алгоритм решения для любого типа заданий №14.
Целесообразно задавать систему координат специальным способом для разных объектов.
Целесообразно изображать плоскость Оху и основание геометрического тела в ней отдельно.
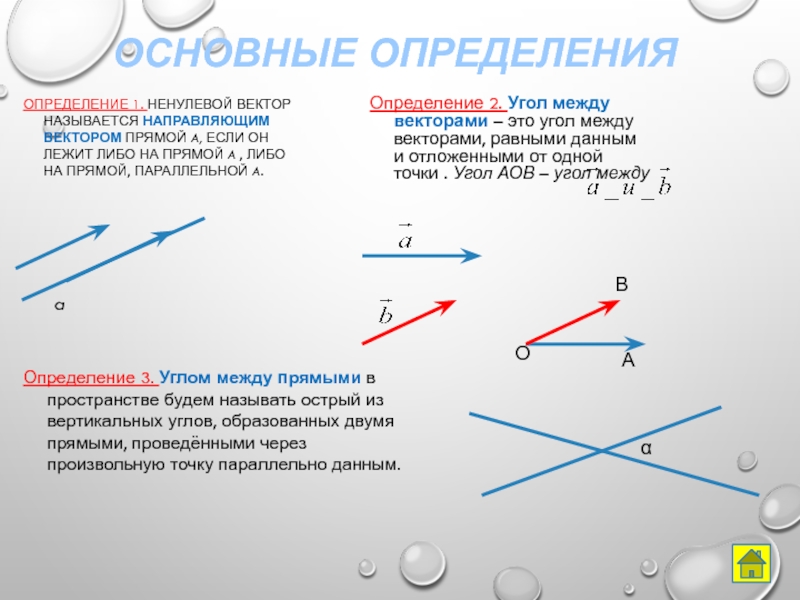
Слайд 6Основные определения
Определение 1. Ненулевой вектор называется направляющим вектором прямой a, если
он лежит либо на прямой a , либо на прямой, параллельной a.
a
Определение 2. Угол между векторами – это угол между векторами, равными данным и отложенными от одной точки . Угол АОВ – угол между
А
О
В
Определение 3. Углом между прямыми в пространстве будем называть острый из вертикальных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.
α
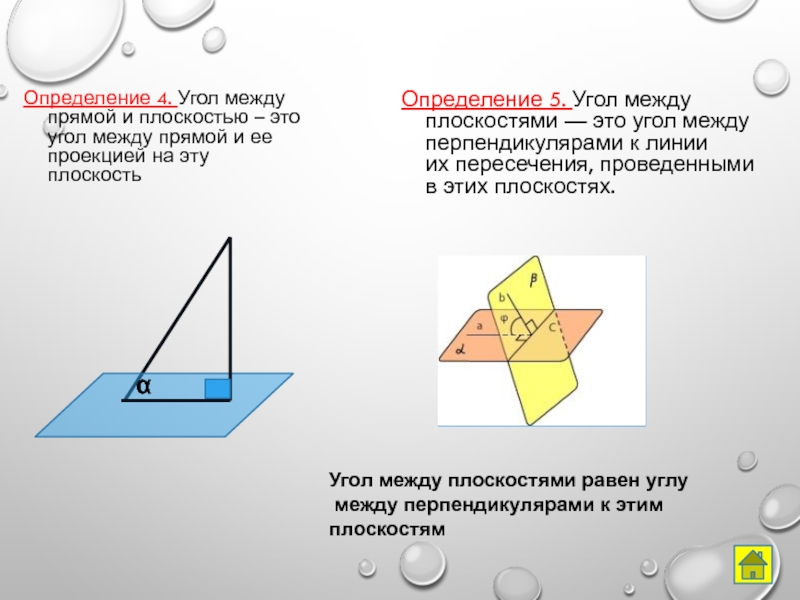
Слайд 7Определение 4. Угол между прямой и плоскостью – это угол между
прямой и ее проекцией на эту плоскость
Определение 5. Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.
Угол между плоскостями равен углу
между перпендикулярами к этим плоскостям
Слайд 8Определение 6. Отрезок, имеющий концы на двух скрещивающихся прямых и перпендикулярный
к ним, называется общим перпендикуляром скрещивающихся прямых.
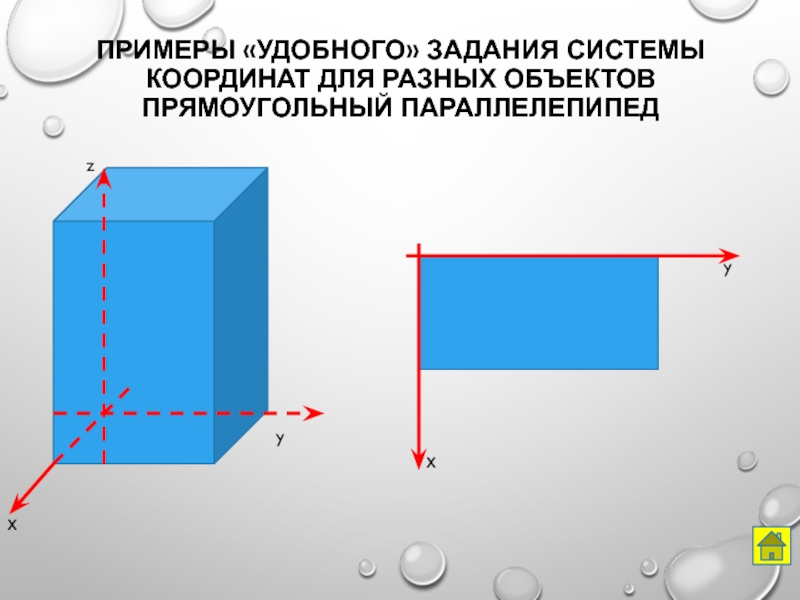
Слайд 9Примеры «удобного» задания системы координат для разных объектов
Прямоугольный параллелепипед
х
y
z
Слайд 13Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при
пересечении прямых.
Пусть – тот из углов, который не превосходит любой из трех остальных углов. Тогда говорят, что угол между пересекающимися прямыми равен
a
b
Слайд 14Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными
данным скрещивающимися.
Через произвольную точку М проведем прямые m и n, соответственно параллельные прямым a и b.
Угол между скрещивающимися прямыми a и b равен
a
b
b
M
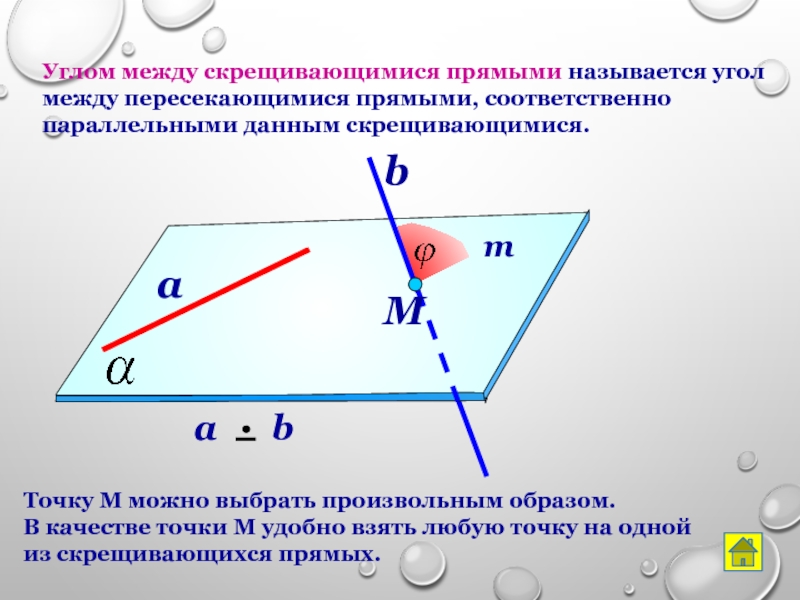
Слайд 15Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными
данным скрещивающимися.
Точку М можно выбрать произвольным образом.
В качестве точки М удобно взять любую точку на одной из скрещивающихся прямых.
a
b
M
m
Слайд 17Угол между прямыми (обозначим α)
Используем формулу:
Где
{x1;y1;z1} – координаты направляющего вектора
первой прямой
{x2;y2;z2} – координаты направляющего вектора второй прямой
Так как угол между прямыми выбираем острый,
то косинус положителен
{x2;y2;z2} – координаты направляющего вектора второй прямой
Так как угол между прямыми выбираем острый,
то косинус положителен
К решению примера 1
К решению примера 2
Слайд 18 Угол между прямой и плоскостью
а
а1
φ0
с
φ
H
M
O
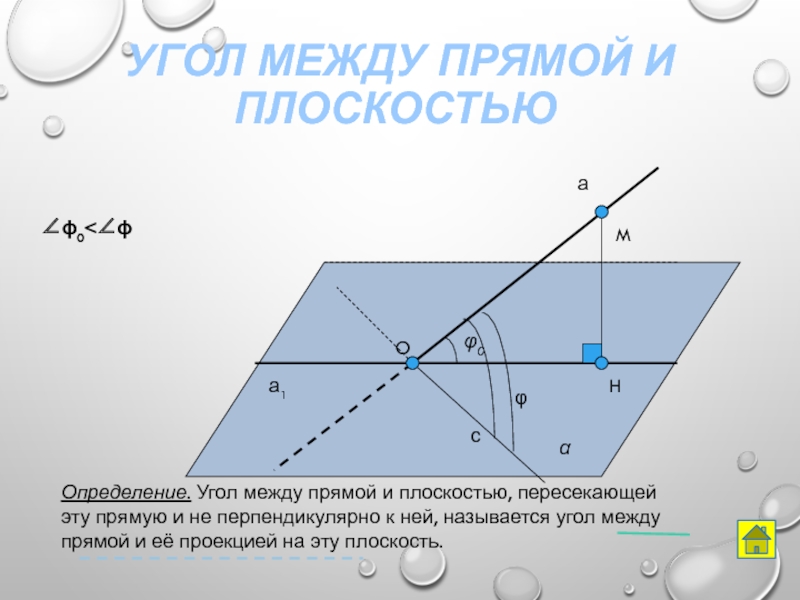
Определение. Угол между прямой и плоскостью,
пересекающей эту прямую и не перпендикулярно к ней, называется угол между прямой и её проекцией на эту плоскость.
0<
Слайд 19Как построить угол между прямой а и плоскостью ?
а
О
М
Н
а1
План
Выбрать т. М
на прямой а
Опустить МН
Построить ОН=а1- проекция прямой а
=(а, )- искомый.
Опустить МН
Построить ОН=а1- проекция прямой а
=(а, )- искомый.
Угол между прямой и плоскостью
Слайд 20 Угол между прямой и плоскостью
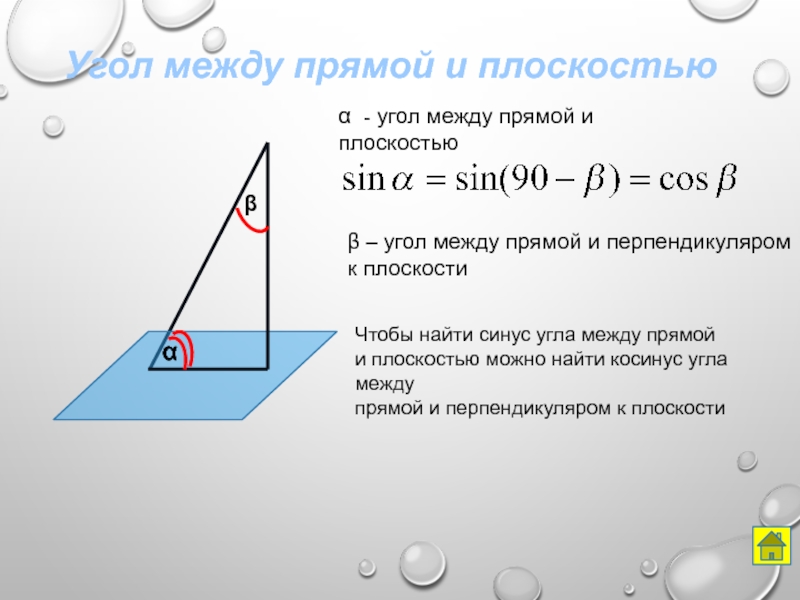
α - угол между прямой и
плоскостью
β – угол между прямой и перпендикуляром
к плоскости
Чтобы найти синус угла между прямой
и плоскостью можно найти косинус угла между
прямой и перпендикуляром к плоскости
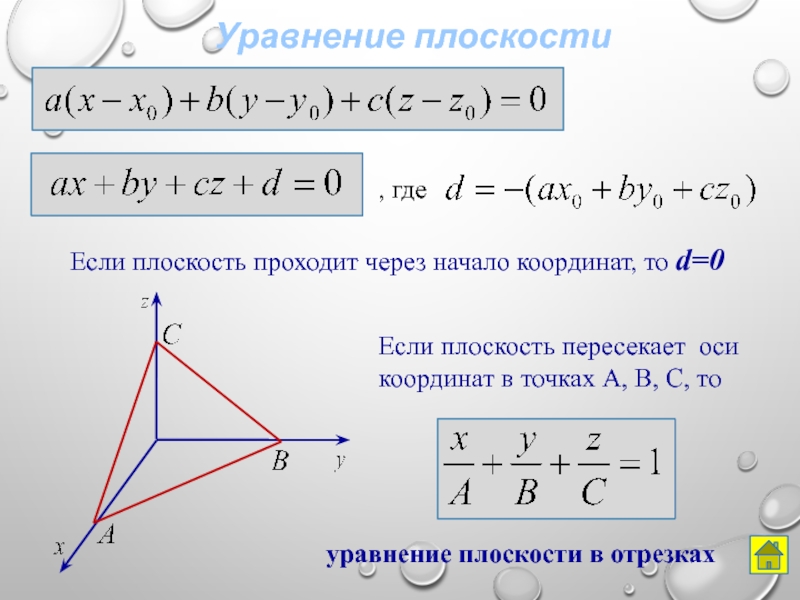
Слайд 23Уравнение плоскости
Если плоскость проходит через начало координат, то d=0
Если плоскость пересекает
оси координат в точках А, В, С, то
уравнение плоскости в отрезках
Слайд 24Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при
пересечении двугранного угла плоскостью, перпендикулярной его ребру.
А
В
N
М
Двугранный угол АВNМ, где ВN – ребро, точки А и М лежат в гранях двугранного угла
Угол SFX – линейный угол двугранного угла
Слайд 25Алгоритм построения линейного угла
D
E
Угол РОК – линейный угол двугранного угла РDEК.
Плоскость
линейного угла (РОК) DE.
Слайд 261) Как угол между прямыми, лежащими в этих плоскостях и перпендикулярными
к линии их пересечения;
Угол между пересекающимися плоскостями можно вычислить:
4) Используя ключевые задачи;
3) Используя координатно –векторный метод;
2) Как угол треугольника, если удается включить линейный угол в некоторый треугольник;
Слайд 27Угол между плоскостями
Угол между плоскостями равен углу между перпендикулярами к этим
плоскостям
Слайд 28Задача 1 (угол между прямыми)
В правильной шестиугольной призме А…F1, все ребра
которой раны 1, найдите косинус угла между прямыми АВ1 и ВС1
1
1/2
Слайд 29Решение задачи 1
1
1/2
Ответ: 0,75
Введем прямоугольную систему координат (см. рисунок)
x
y
Посмотреть формулу
Слайд 30В кубе A...D1 найдите тангенс угла между прямой AC1 и плоскостью
BDD1.
А
D
С
В
Задача 2 (угол между прямой и плоскостью).
Слайд 31Введем прямоугольную систему координат (см. рисунок)
А
D
С
В
А(1;0;0)
С(0;1;0)
С1(0;1;1)
Пусть α – искомый угол)
Посмотреть формулу
Решение
задачи 2
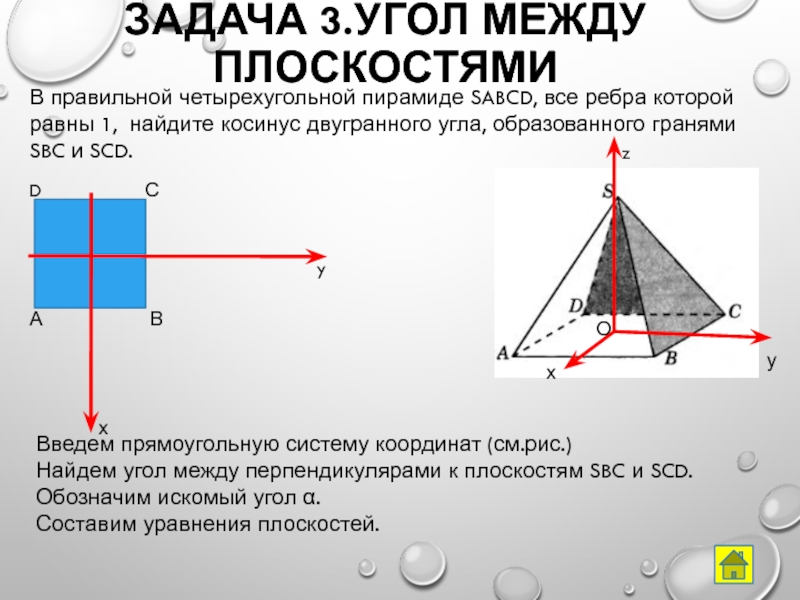
Слайд 32Задача 3.Угол между плоскостями
В правильной четырехугольной пирамиде SABCD, все ребра которой
равны
1, найдите косинус двугранного угла, образованного гранями
SBC и SCD.
SBC и SCD.
Введем прямоугольную систему координат (см.рис.)
Найдем угол между перпендикулярами к плоскостям SBC и SCD. Обозначим искомый угол α.
Составим уравнения плоскостей.
О
Слайд 33Решение задачи 3
(1) aх+by+cz+d=0 – общий вид уравнения плоскости
Т.к. точки S,B,C
принадлежат плоскости SBC,
то их координаты удовлетворяют уравнению (1)
то их координаты удовлетворяют уравнению (1)
Составим и решим систему уравнений
Неизвестных 4, уравнений 3
Пусть d=1
Слайд 34Решение задачи 3(продолжение)
Аналогично найдем координаты
Вектора, перпендикулярного
плоскости SCD
