- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Методы решения иррациональных уравнений, профильный уровень 10 класс
Содержание
- 1. Методы решения иррациональных уравнений, профильный уровень 10 класс
- 2. Работаем устно
- 3. Устная работаМожно ли, не решая уравнений, сделать вывод о неразрешимости предложенных уравнений:
- 4. Методы решения иррациональных уравненийВведение новой переменнойИсследование ОДЗУмножение
- 5. Методы решения иррациональных уравненийИспользование свойств монотонности функцийФункционально
- 6. Введение новой переменнойа2 -2а – 3 =0а1
- 7. Ответ: [5; 10]
- 8. Введение новой переменной Решить уравнение.Пусть х2+ 3х-
- 9. Решить уравнениеИсследование ОДЗРешение.Замечаем, что ОДЗ уравнения
- 10. Умножение обеих частей уравнения на сопряженный множительРешить
- 11. (1) | ∙ х=0
- 12. Сведение к системе рациональных уравнений с помощью
- 13. Слайд 13
- 14. Выделение полного квадратаРешить уравнение Заметим, что Следовательно,
- 15. Использование свойств монотонности функцийf(x) =
- 16. Использование свойств монотонности функцийРешить уравнение
- 17. Графический метод Решите графически уравнение 1) Строим
- 18. Домашнее задание Решить систему уравненийРешите уравнения:
Слайд 3Устная работа
Можно ли, не решая уравнений, сделать вывод о неразрешимости предложенных
Слайд 4Методы решения иррациональных уравнений
Введение новой переменной
Исследование ОДЗ
Умножение обеих частей уравнения на
Сведение уравнения к системе рациональных уравнений с помощью введения переменной.
Выделение полного квадрата
Слайд 5Методы решения иррациональных уравнений
Использование свойств монотонности функций
Функционально - графический метод
Метод равносильных
Метод возведения обеих частей уравнения в одну и ту же степень
Слайд 6Введение новой переменной
а2 -2а – 3 =0
а1 = -1 не удовлетворяет
а2 = 3
х + 32 = 81
х = 49
Ответ: 49.
Слайд 8Введение новой переменной
Решить уравнение.
Пусть х2+ 3х- 6 = t ,
тогда
Отсюда, t1=4, t2=36.
Проверка: t=36 – посторонний корень.
Выполняем обратную подстановку
х2+3х-6=4
Отсюда, х1= - 5, х2=2.
Слайд 9
Решить уравнение
Исследование ОДЗ
Решение.
Замечаем, что ОДЗ уравнения состоит из одной точки х=1.
Проверкой
х=1 – решение уравнения.
Слайд 10Умножение обеих частей уравнения на сопряженный множитель
Решить уравнение
Умножим обе части уравнения
Проверкой убеждаемся, что х = 1 является корнем данного уравнения.
Слайд 12Сведение к системе рациональных уравнений с помощью введения переменной
Решить уравнение
Замена
Тогда u+v=3.
Так как u3=x-2, v2=x+1,
то v2 – u3 =3. Итак, в новых переменных имеем
Значит, х=3.
Слайд 14Выделение полного квадрата
Решить уравнение
Заметим, что
Следовательно, имеем уравнение:
или
Решением первой системы
Ответ:
Слайд 15Использование свойств монотонности функций
f(x) =
g(x)= 5 - x, - убывает на D(g).
Уравнение f(x)=g(x) имеет не более одного корня.
4. Подбором находим, что X=2.
Ответ. 2.
Слайд 16Использование свойств монотонности функций
Решить уравнение
Если функция
Отсюда следует, что уравнение и(х) = v(x), где и(х) - возрастающая, a v(x) – убывающая функции, либо не имеет решений, либо имеет единственное решение.
Подбором находим, что х=2. Это единственное
решение.
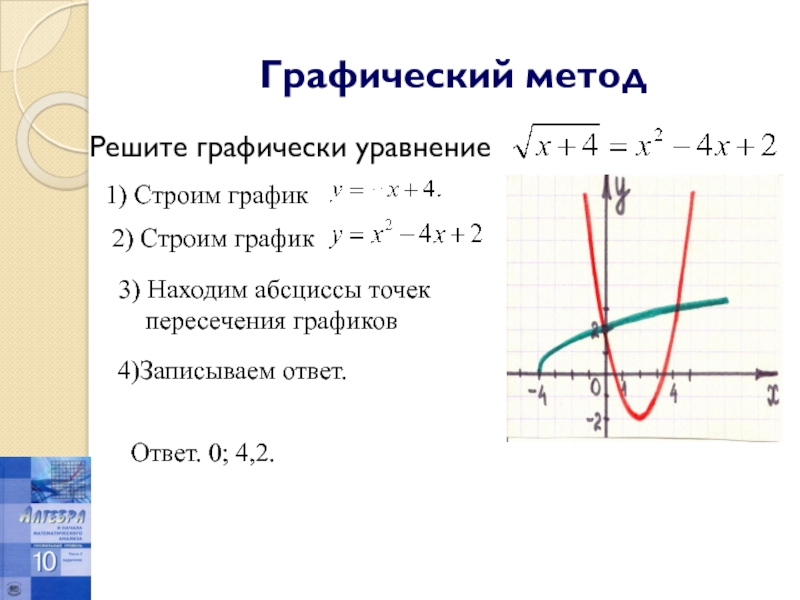
Слайд 17Графический метод
Решите графически уравнение
1) Строим график
2) Строим график
3)
пересечения графиков
4)Записываем ответ.
Ответ. 0; 4,2.






![Методы решения иррациональных уравнений, профильный уровень 10 класс Ответ: [5; 10] Ответ: [5; 10]](/img/thumbs/f1c03aeb85e2b5fcdc615755594f6198-800x.jpg)