тангенс, котангенс угла, основные тригонометрические тождества, формулы приведения”
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Методическая разработка открытого урока на тему: Радианная мера угла
Содержание
- 1. Методическая разработка открытого урока на тему: Радианная мера угла
- 2. Цели урока:Сформировать умения и навыкирассмотреть понятия радианной
- 3. Что такое тригонометрия?Для чего она мне нужна?
- 4. Тригонометрические функции в тригонометрии.Что такое синус,
- 5. Вспомним:авсСинус острого угла в прямоугольном треугольнике
- 6. Слайд 6
- 7. Слайд 7
- 8. Центральный угол, опирающийся на дугу, длина которой
- 9. Если угол содержит α радиан, то
- 10. Слайд 10
- 11. Слайд 11
- 12. Выразите угол в радианах с помощью π:45°=150°=90°=360°=30°=270°=135°=60°=180°=- 210°=- 720°=
- 13. Найдите градусную меру угла, радианная мера которого равна:18°72°540°300°108°
- 14. Задача 2: Силы в 40
- 15. Тригонометрияраздел математики, изучающий соотношение сторон и углов
- 16. КотангенсТангенсСинусКосинус
- 17. Тригонометрия – математическая дисциплина, изучающая зависимость между
- 18. Самостоятельная работа1. Переведите в радианную меру углы:1)
- 19. С АНРИС. 1С РИС. 2Н cos2 С
- 20. Слайд 20
- 21. Слайд 21
- 22. Рассмотрим в прямоугольной системе координат окружность единичного
- 23. Слайд 23
- 24. ху11
- 25. Синус угла определяется как ордината точки
- 26. Понятие синуса встречается уже в III в.
- 27. 11-1-1
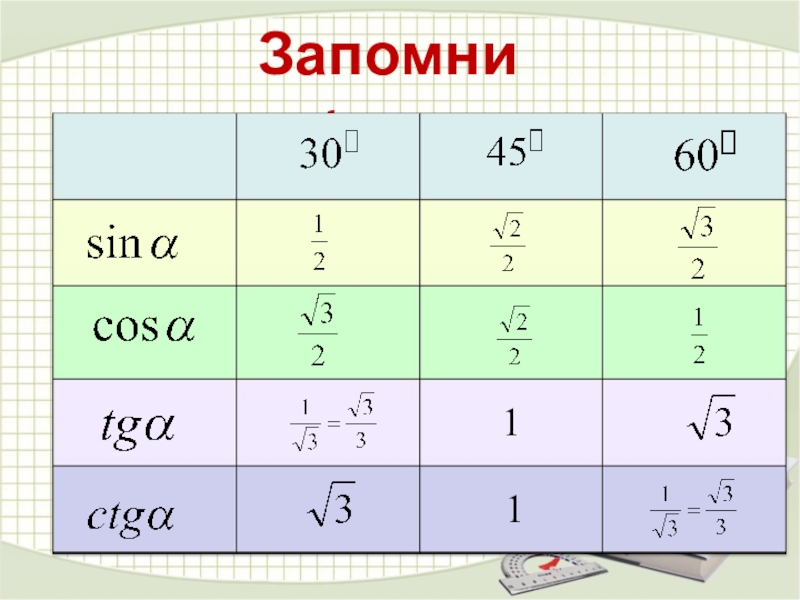
- 28. Запомним !11
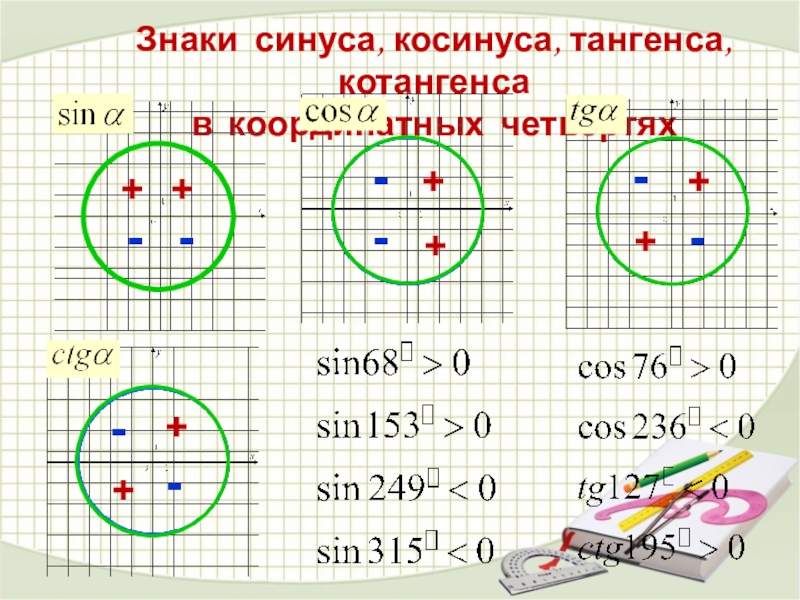
- 29. Знаки синуса, косинуса, тангенса, котангенсав координатных четвертях++++++++--------
- 30. Тренинг. Решение упражнений. Алгоритм решения
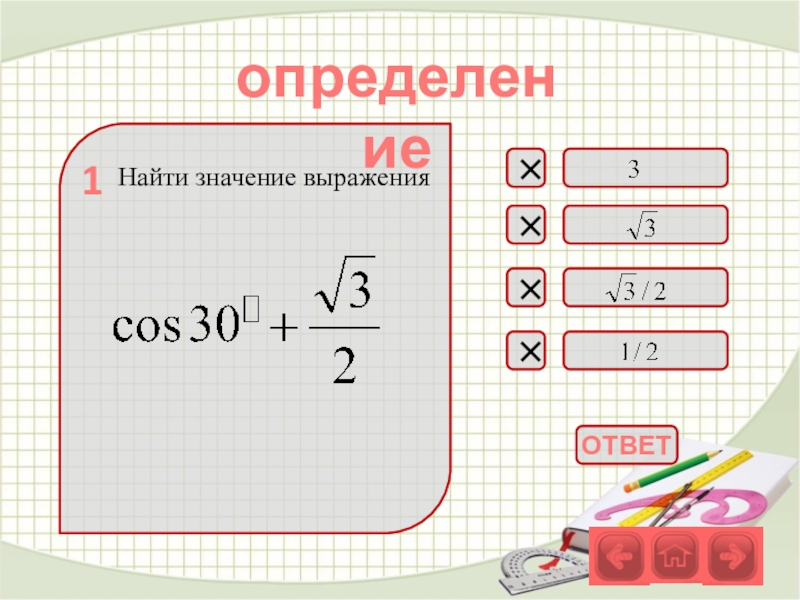
- 31. Найти значение выраженияопределение1
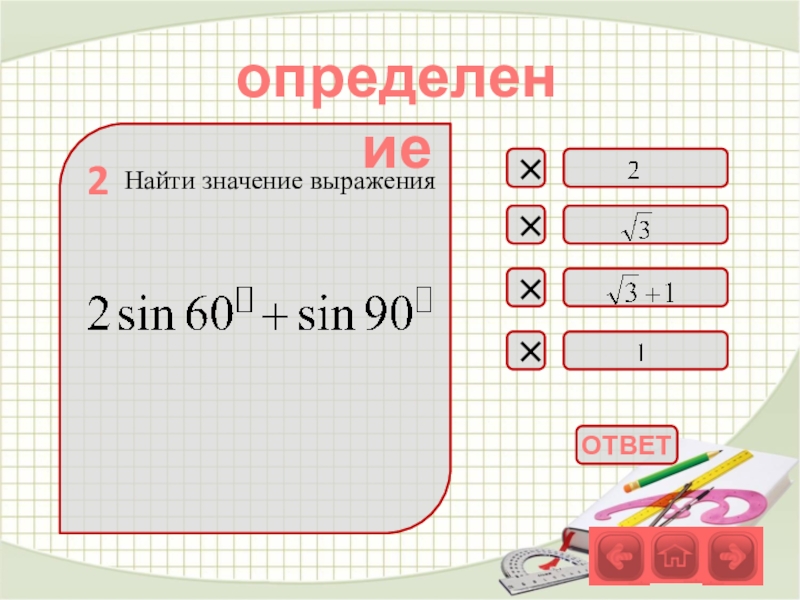
- 32. Найти значение выраженияопределение2
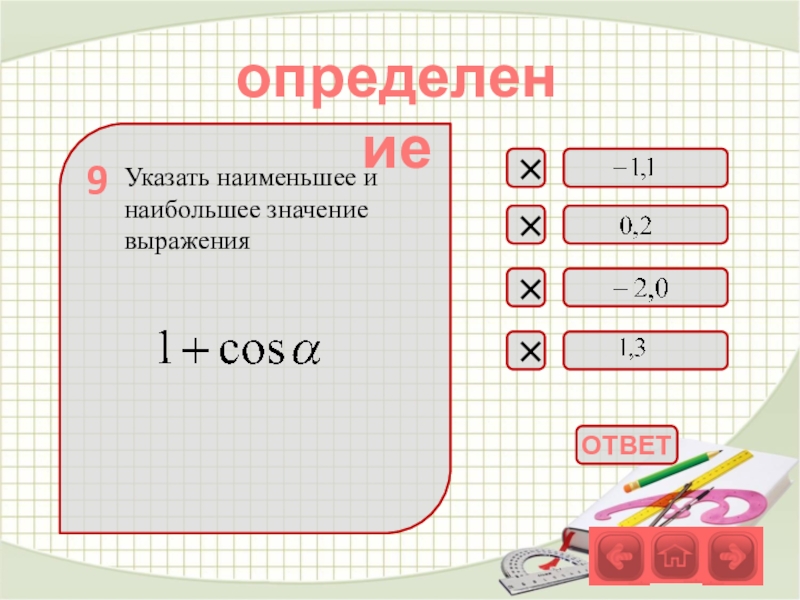
- 33. Указать наименьшее и наибольшее значение выраженияопределение9
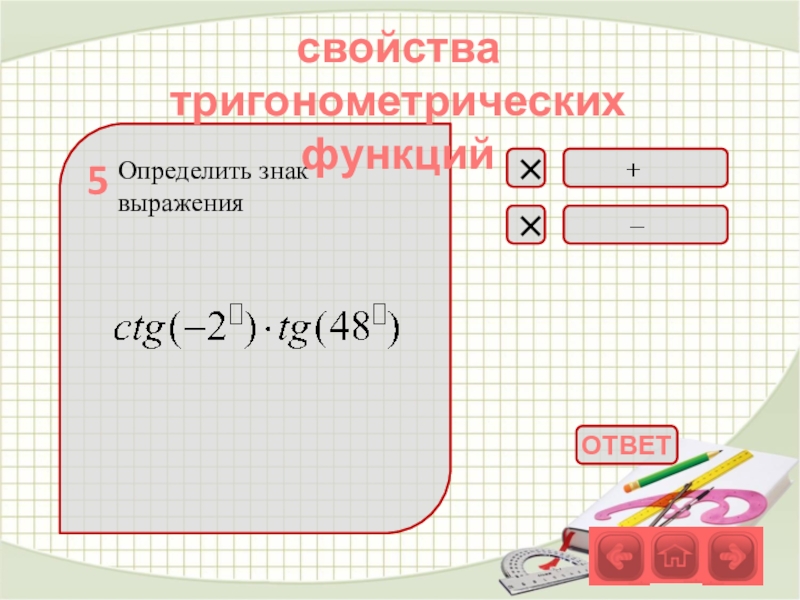
- 34. Определить знак выражениясвойства тригонометрических функций5
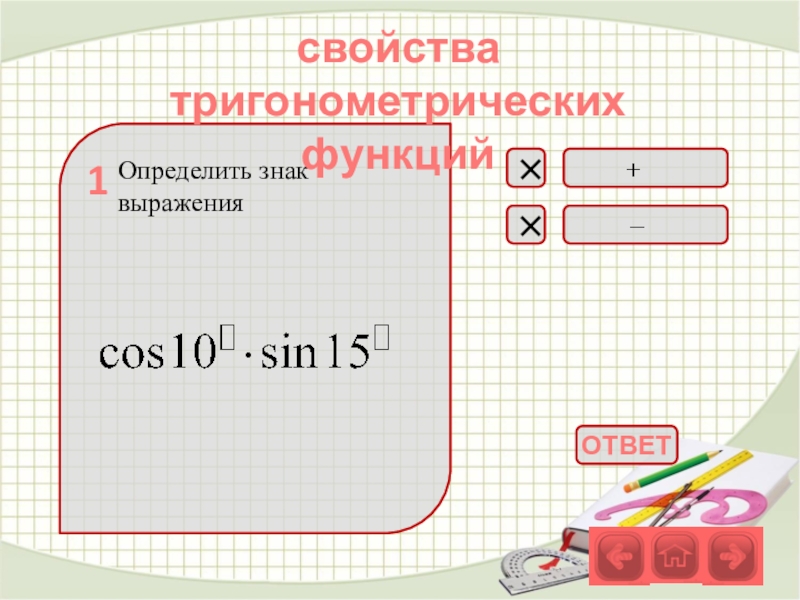
- 35. Определить знак выражениясвойства тригонометрических функций1
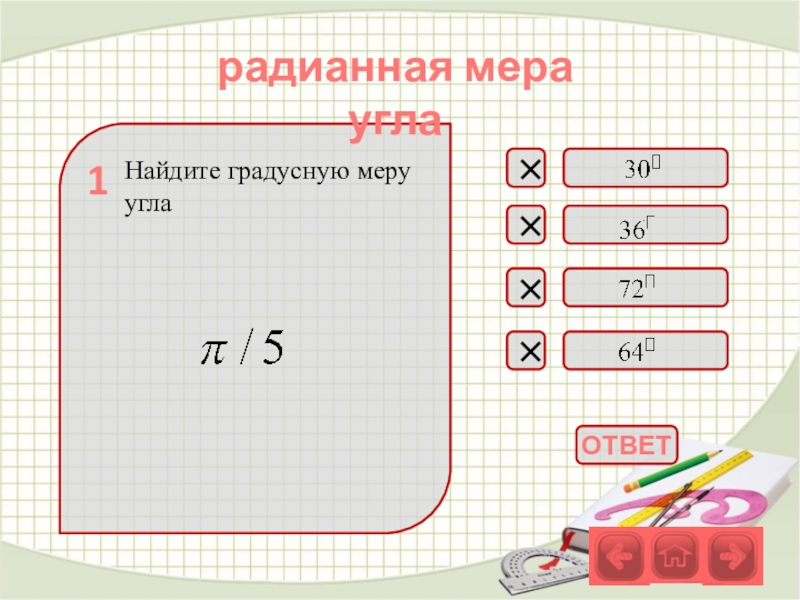
- 36. Найдите градусную меру угла1радианная мера угла
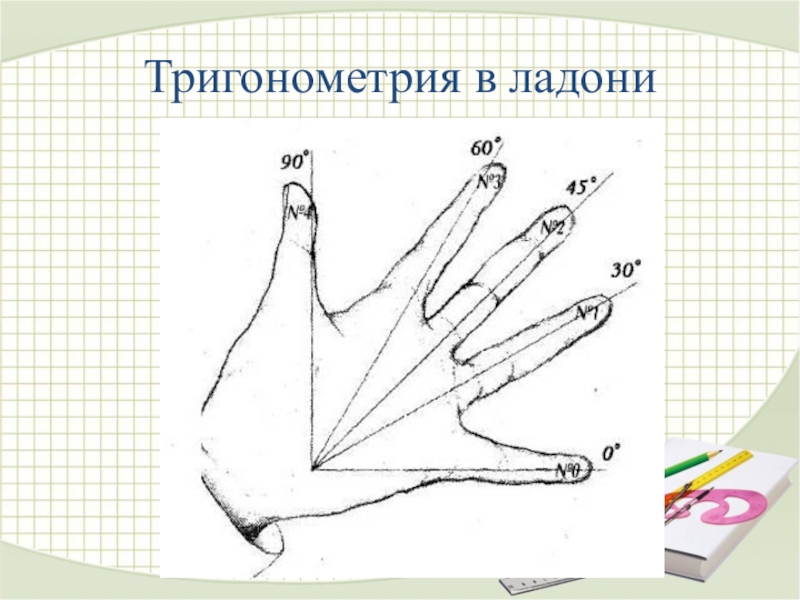
- 37. Тригонометрия в ладони
- 38. Слайд 38
- 39. Синусом угла α называется отношение ординаты точки
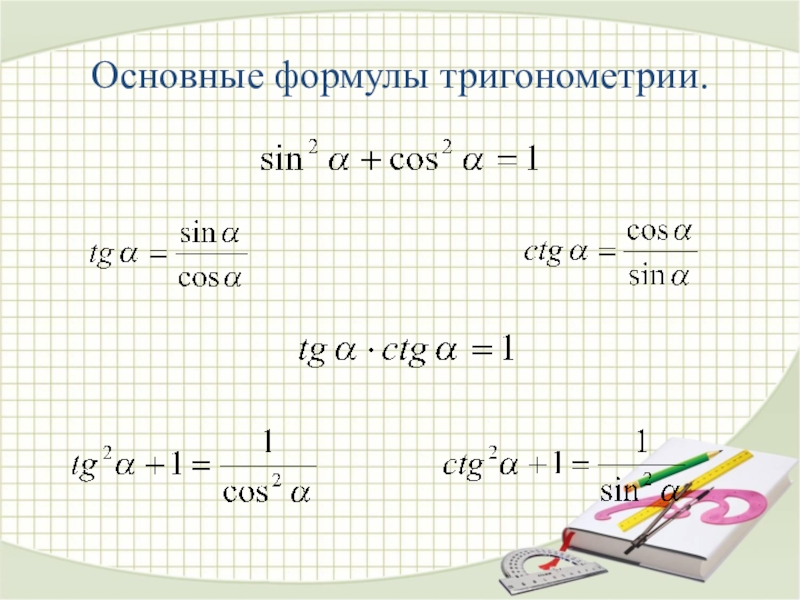
- 40. Основные формулы тригонометрии.
- 41. Домашнее задание1) Выучить формулы перевода из градусной
- 42. Ответьте на вопросы:1) Что означает «тригонометрия»?2) Разделом
- 43. Спасибо за внимание!Не забывайте готовиться к урокам!
- 44. Слайд 44
Цели урока:Сформировать умения и навыкирассмотреть понятия радианной меры угла, вращательного движения, синуса, косинуса, тангенса, котангенса угла, основные тригонометрические тождества, формулы приведениясформировать умения и навыки применять тригонометрические тождества, формулы приведения
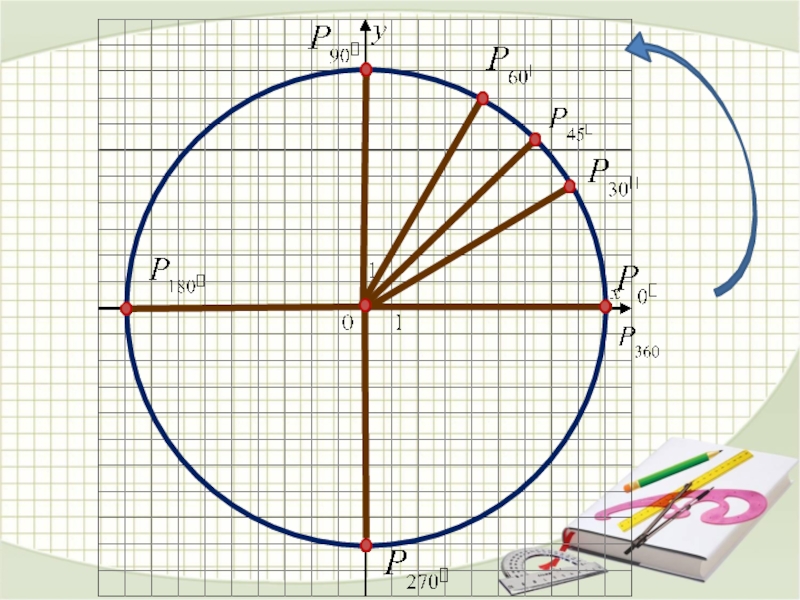
Слайд 1Тема урока:
”Основные понятия тригонометрии: радианная мера угла, вращательное движение, синус, косинус,
Слайд 2Цели урока:
Сформировать умения и навыки
рассмотреть понятия радианной меры угла, вращательного движения,
синуса, косинуса, тангенса, котангенса угла, основные тригонометрические тождества, формулы приведения
сформировать умения и навыки применять тригонометрические тождества, формулы приведения
Слайд 4
Тригонометрические функции в тригонометрии.
Что такое синус, косинус, тангенс и котангенс?
Мальчик
поднимается в гору. АВ-склон горы, ВС-высота горы.
Задача: Как определить крутизну горы?
Можно измерить высоту горы ВС.
2. Но достаточно ли это?
3. Необходимо знать и длину склона АВ
4. Как изменится крутизна горы , если увеличить высоту ВС и уменьшить длину склона горы.
ВЫВОД: Чем больше высота горы ВС и меньше длина склоны АВ, тем круче гора, т.е. тем больше угол
и наоборот, чем длиннее склон горы и меньше высота горы, тем меньше крутизна горы, значит и угол
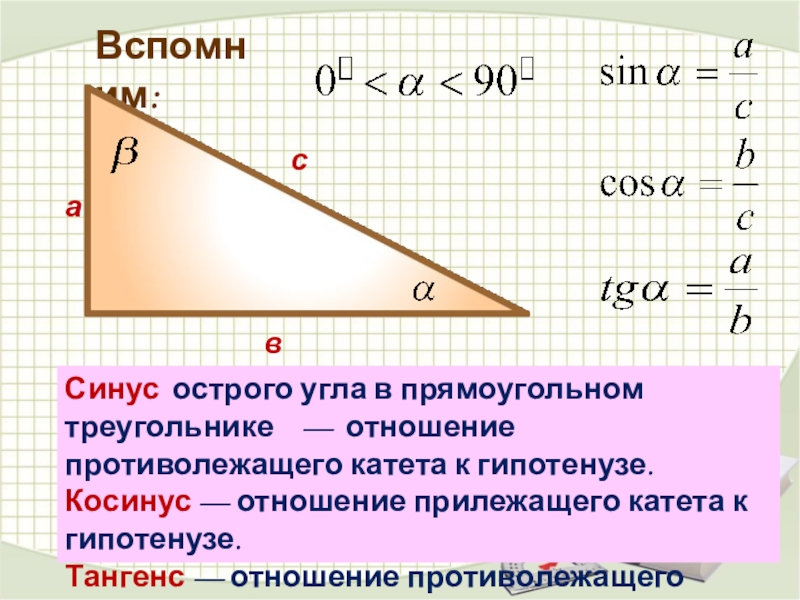
Слайд 5Вспомним:
а
в
с
Синус острого угла в прямоугольном треугольнике — отношение противолежащего катета
к гипотенузе.
Косинус — отношение прилежащего катета к гипотенузе.
Тангенс — отношение противолежащего катета к прилежащему.
Косинус — отношение прилежащего катета к гипотенузе.
Тангенс — отношение противолежащего катета к прилежащему.
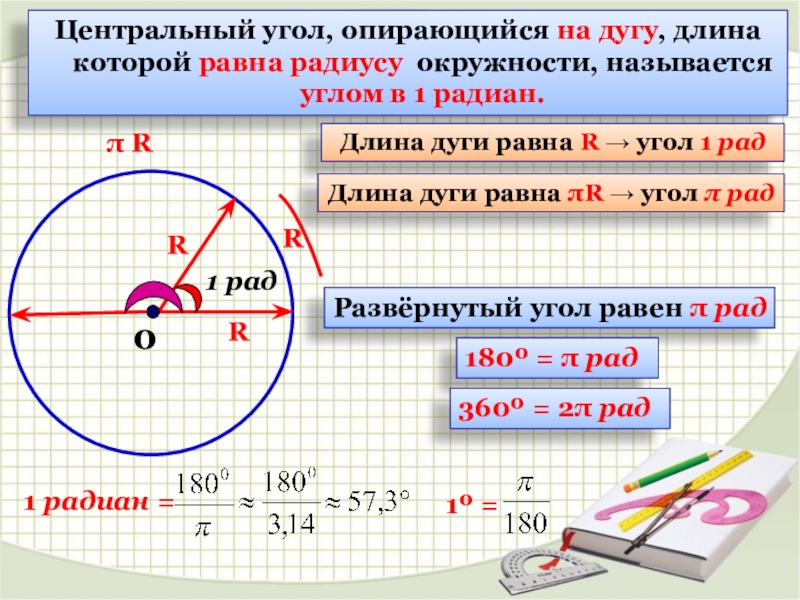
Слайд 8Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется
углом в 1 радиан.
0
R
R
R
1 рад
Длина дуги равна R → угол 1 рад
Длина дуги равна πR → угол π рад
Развёрнутый угол равен π рад
π R
180º = π рад
360º = 2π рад
1 радиан =
1º =
Слайд 9 Если угол содержит α радиан, то его градусная мера равна
Если угол содержит α градусов, то его радианная мера равна
Слайд 12Выразите угол в радианах с помощью π:
45°=
150°=
90°=
360°=
30°=
270°=
135°=
60°=
180°=
- 210°=
- 720°=
Слайд 14Задача 2:
Силы в 40 Н и 56 Н
действуют на одну и ту же точку тела под прямым углом. Найдите равнодействующую этих сил и углы, образуемые ею с каждой из составляющих.
Решение:
Т.к угол между этими силами равен 90, то отобразив проекцию равнодействующей этих сил на оси Х и У, выведем следующее выражение:
F2 =F12 + F22 ;
F2 =4736 H;
F =69 H.
Ответ: 69 Н, 450 ,450
x
Y
Слайд 15Тригонометрия
раздел математики, изучающий соотношение сторон и углов в треугольнике
(«три» - три,
«гониа» - угол, «метриа» - измеряю)
Слайд 17Тригонометрия – математическая дисциплина, изучающая зависимость между сторонами и углами треугольника.
Тригонометрические
вычисления применяются практически во всех областях геометрии, физики и инженерного дела, при измерении расстояний до недалёких звёзд в астрономии, между ориентирами в географии, при контроле системы навигации, в теории музыки, акустике, оптике, электронике, теории вероятностей, статистике, биологии, медицине (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтике, химии, сейсмологии, метеорологии, океанологии, картографии, архитектуре, экономике, электронной технике, машиностроении, компьютерной графике.
Слайд 18Самостоятельная работа
1. Переведите в радианную меру углы:
1) 60
2) 145
3)
240
I вариант
II вариант
1) 320
2) 105
3) 40
2. Переведите в градусную меру углы:
1)
2)
1)
2)
Слайд 19
С
А
Н
РИС. 1
С
РИС. 2
Н
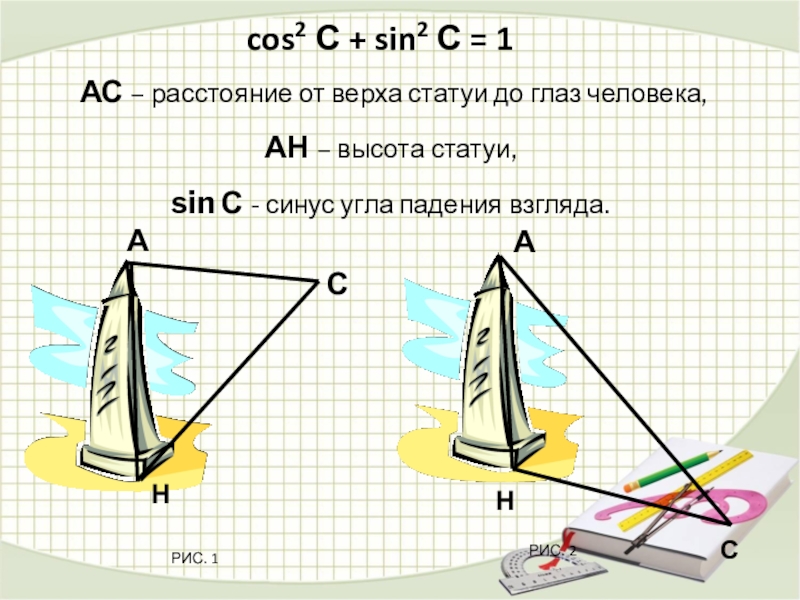
cos2 С + sin2 С =
1
АС – расстояние от верха статуи до глаз человека,
АН – высота статуи,
sin С - синус угла падения взгляда.
А
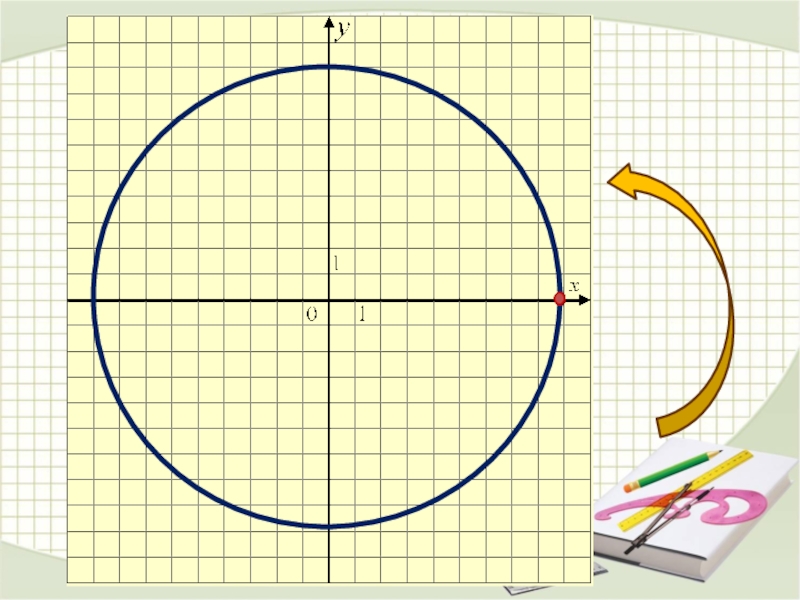
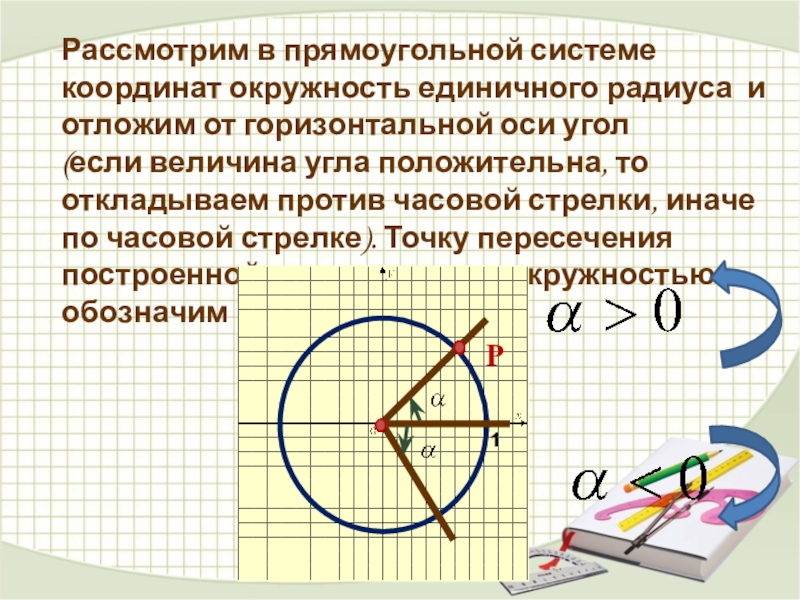
Слайд 22Рассмотрим в прямоугольной системе координат окружность единичного радиуса и отложим от
горизонтальной оси угол
(если величина угла положительна, то откладываем против часовой стрелки, иначе по часовой стрелке). Точку пересечения построенной стороны угла с окружностью обозначим Р.
(если величина угла положительна, то откладываем против часовой стрелки, иначе по часовой стрелке). Точку пересечения построенной стороны угла с окружностью обозначим Р.
1
Р
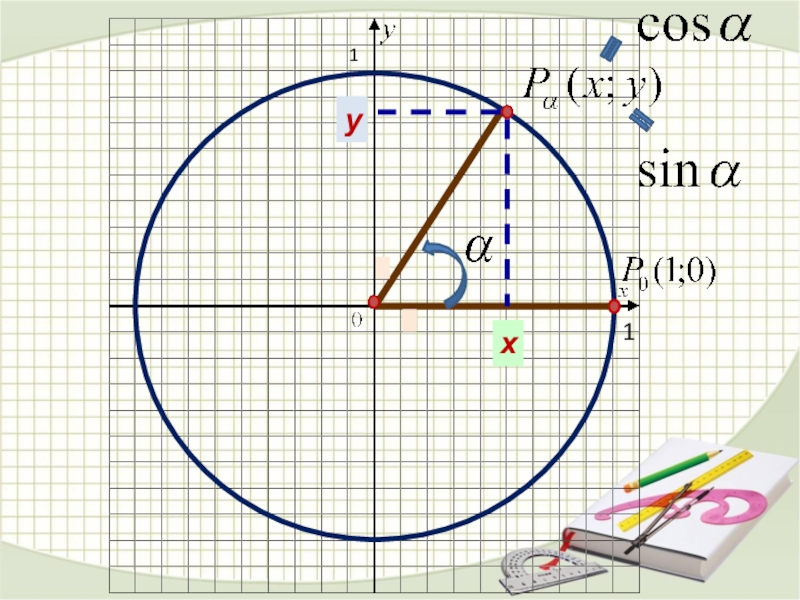
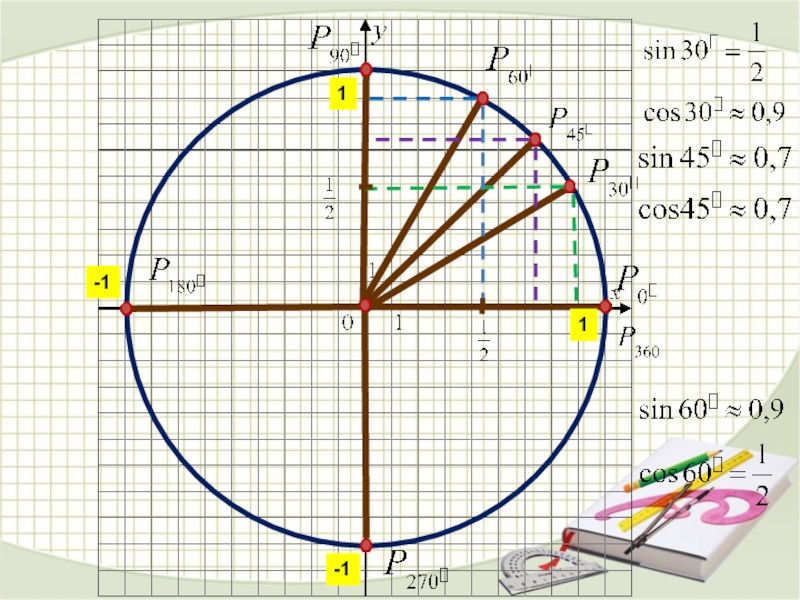
Слайд 25Синус угла определяется как ордината
точки
Косинус — абсцисса точки
Тангенс – отношение ординаты к абсциссе
точки
Котангенс – отношение абсциссы к ординате
точки
Слайд 26Понятие синуса встречается уже в III в. до н. э.
и
имел название джива (тетева лука) ,
в IX в. заменено на арабское слово
джайб (выпуклость) , XII в. заменено на латинское
синус (изгиб, кривизна) .
Косинус – это дополнительный синус.
Тангенс переводится с латинского
как «касающийся»
в IX в. заменено на арабское слово
джайб (выпуклость) , XII в. заменено на латинское
синус (изгиб, кривизна) .
Косинус – это дополнительный синус.
Тангенс переводится с латинского
как «касающийся»
Слайд 30Тренинг. Решение упражнений.
Алгоритм решения
Решение
Какие знаки имеют следующие выражения:
1) cos 150;
2) sin 320;
3) tg 220;
4) ctg 400.
Упростить:
Вычислить: По таблице значений находим значение аргумента каждой тригонометрической функции:
Какие знаки имеют следующие выражения:
1) cos 150;
2) sin 320;
3) tg 220;
4) ctg 400.
Упростить:
Вычислить: По таблице значений находим значение аргумента каждой тригонометрической функции:
1) 90<150<180 (II четверть), cos 150<0;
2) 270<320<360 (IV четверть), sin320<0;
3) 180<220<270 (III четверть), tg220>0;
4) 360<400<360+90 (I четверть), ctg 400>0.
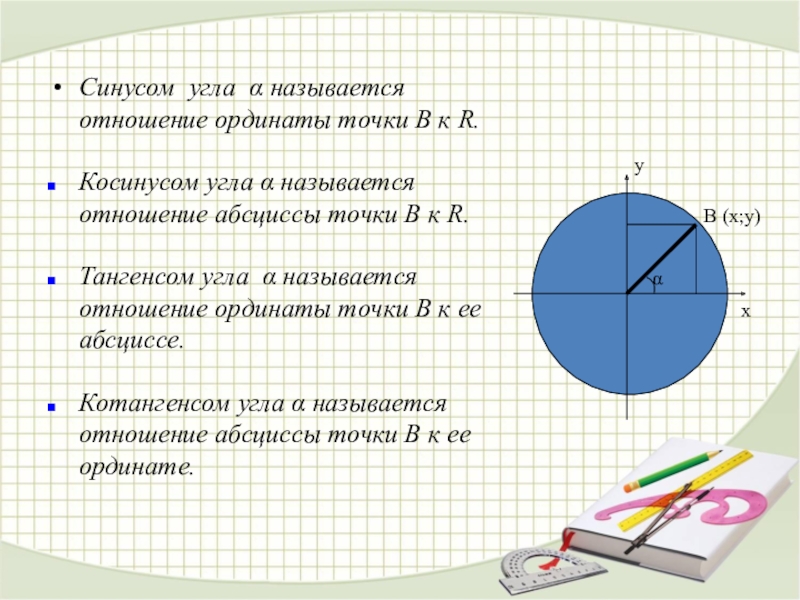
Слайд 39Синусом угла α называется отношение ординаты точки В к R.
R
Косинусом угла
α называется отношение абсциссы точки В к R.
Тангенсом угла α называется отношение ординаты точки В к ее абсциссе.
Котангенсом угла α называется отношение абсциссы точки В к ее ординате.
Слайд 41Домашнее задание
1) Выучить формулы перевода из градусной меры угла в радианную
и обратно
2) Переведите в радианную меру углы: 75, 15, 130, 220, 340
3) Переведите в градусную меру углы:
, , , ,
Слайд 42Ответьте на вопросы:
1) Что означает «тригонометрия»?
2) Разделом какой науки являлась тригонометрия
в начале развития?
3) Почему окружность «единичная»?
4)Какие единицы измерения углов Вы знаете?
5) Чему равно радиан?
6) Как перевести из градусной меры в радианную и обратно?
7) Было ли интересно на уроке?
Слайд 43Спасибо за внимание!
Не забывайте готовиться к урокам!
Тема следующего урока
«Синус,косинус
и тангенс суммы и разности двух углов.Синус и косинус двойного угла»
Написать реферат на данную тему, о её применении и привести примеры.
Удачи!
Написать реферат на данную тему, о её применении и привести примеры.
Удачи!
http://www.myshared.ru/slide/719041/
