нем есть
Мария, Сулейман, Остап, Берта, Бей и Бендер.
Сколько имен должен написать милиционер, чтобы среди них обязательно оказалось имя «преступника»?
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Материалы по САНПИН. Комбинаторика
Содержание
- 1. Материалы по САНПИН. Комбинаторика
- 2. Задача 2 (размещения). Десять стульев были проданы
- 3. Слайд 3
- 4. Сколько стратегий поиска стульев (порядка поиска стульев)
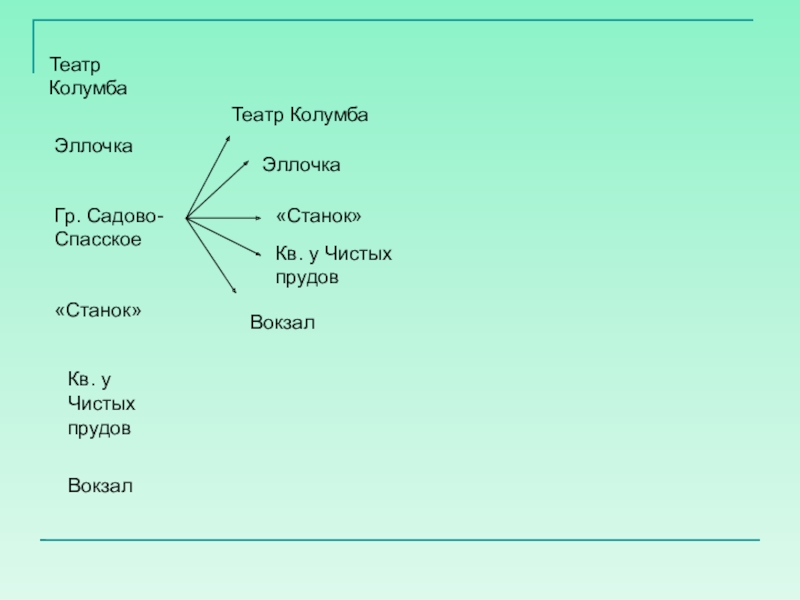
- 5. Театр КолумбаЭллочкаГр. Садово-Спасское«Станок»Кв. у Чистых прудовВокзалТеатр КолумбаЭллочка«Станок»Кв. у Чистых прудовВокзал
- 6. Ответ к задаче 2- вариантов стратегий просчитал Остап Бендер мгновенно.
- 7. Перестановки - комбинации из n элементов, отличающиеся
- 8. Сравнительная таблица подсчета числа перестановок и размещений
- 9. Сочетания
- 10. Задача 3: Членами подпольной организации
- 11. СочетанияКомбинации по m различных элементов, выбранных их
- 12. Задача 3: Членами подпольной организации
- 13. Слайд 13
- 14. Ответ к задаче 3:
- 15. ПерестановкиФормула для подсчета количества всевозможных перестановок:
- 16. РазмещенияФормула для нахождения количества размещений различных m
- 17. Сочетания Формула для нахождения количества сочетаний m элементов из n:
- 18. На занятии мы узнали Для того,
- 19. Спасибо за внимание!
Задача 2 (размещения). Десять стульев были проданы с аукциона в розницу. Остап Бендер отправил по их следу беспризорников. Он узнал:
Слайд 2Задача 2 (размещения).
Десять стульев были проданы с аукциона в розницу.
Остап Бендер отправил по их следу беспризорников. Он узнал:
Слайд 4
Сколько стратегий поиска стульев (порядка поиска стульев) Остап Бендер смог просчитать
мгновенно, если за один миг он просчитывал все варианты развития событий на два шага вперед?
Слайд 5Театр Колумба
Эллочка
Гр. Садово-Спасское
«Станок»
Кв. у Чистых прудов
Вокзал
Театр Колумба
Эллочка
«Станок»
Кв. у Чистых прудов
Вокзал
Слайд 7Перестановки - комбинации из n элементов, отличающиеся друг от друга только
порядком их расположения
Найти все перестановки цифр числа 1542 и 8362 ( на баллы) и их количество
Размещения - комбинации по m различных элементов, выбранных из множества, содержащего n элементов, которые отличаются друг от друга не только порядком, но и составом элементов
Пример. Всевозможные размещения из трех элементов 123 и 561 по два элемента:12, 13, 21, 23, 31, 32.
А с повторениями + 11, 22, 33
Найти все перестановки цифр числа 1542 и 8362 ( на баллы) и их количество
Размещения - комбинации по m различных элементов, выбранных из множества, содержащего n элементов, которые отличаются друг от друга не только порядком, но и составом элементов
Пример. Всевозможные размещения из трех элементов 123 и 561 по два элемента:12, 13, 21, 23, 31, 32.
А с повторениями + 11, 22, 33
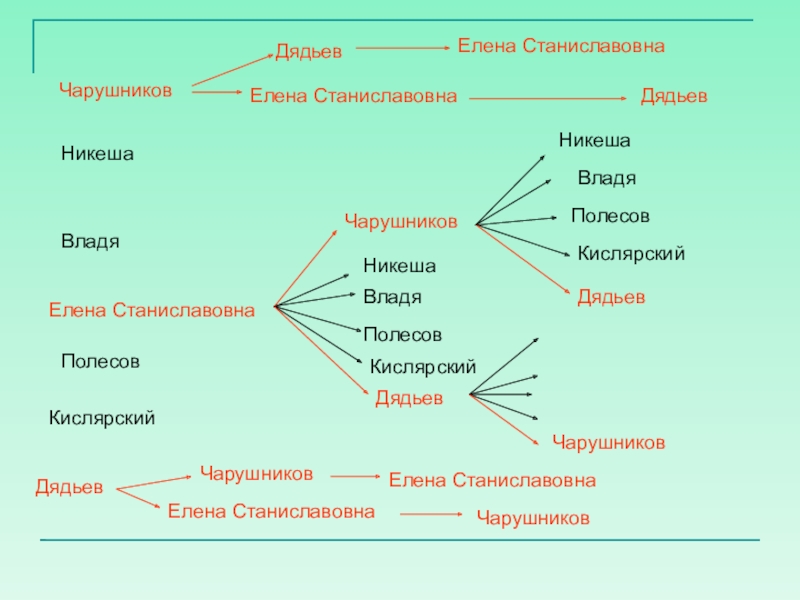
Слайд 10Задача 3: Членами подпольной организации были 7 человек: 1. Чарушников,
2. Никеша,
3. Владя,
4. Полесов,
5. Елена Станиславовна,
6. Кислярский,
7. Дядьев.
Остап устраивал собрания подпольщиков.
На них он приглашал по 3 члена союза.
На каждом собрании Остап Бендер зарабатывал по 1 тысяче рублей.
Сколько денег Остап Бендер сможет собрать с подпольщиков, если будет приглашать на собрания каждый раз новый состав членов подпольной организации?
Слайд 11Сочетания
Комбинации по m различных элементов, выбранных их множества n данных элементов,
которые отличаются друг от друга только составом элементов называются сочетаниями
Слайд 12Задача 3: Членами подпольной организации были 7 человек: 1. Чарушников,
2. Никеша,
3. Владя,
4. Полесов,
5. Елена Станиславовна,
6. Кислярский,
7. Дядьев.
Остап устраивал собрания подпольщиков.
На них он приглашал по 3 члена союза.
На каждом собрании Остап Бендер зарабатывал по 1 тысяче рублей.
Слайд 15Перестановки
Формула для подсчета количества всевозможных перестановок:
Слово «факториал» в переводе с латинского означает «производящий действие».
Перестановками называют комбинации из n элементов, отличающиеся друг от друга только порядком их расположения
Слайд 16Размещения
Формула для нахождения количества размещений различных m элементов из n:
Размещениями называются
комбинации по m различных элементов, выбранных из множества, содержащего n элементов, которые отличаются друг от друга не только порядком, но и составом элементов.
Слайд 18На занятии мы узнали
Для того, чтобы стать Великим комбинатором
надо уметь быстро просчитывать все варианты развития событий.
В этом нам помогают формулы:
1.
2.
3.
В этом нам помогают формулы:
1.
2.
3.
- Формула подсчета количества сочетаний
- формула подсчета количества размещений
- Формула подсчета количества перестановок
