Учитель математики
Гриднева С.Л.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Мастер -класс Применение производной функции
Содержание
- 1. Мастер -класс Применение производной функции
- 2. «Три пути ведут к знанию: путь размышления —
- 3. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ ПРИ РЕШЕНИИ ЗАДАЧ ЕГЭ
- 4. Алексей Николаевич Крылов (1863-1945)«Человек обращается к математике
- 5. -Зачем нужна производная? -Где мы встречаемся с
- 6. «Лишь дифференциальное исчисление дает естествознанию возможность изображать математически не только состояния, но и процессы: движение»Ф.ЭНГЕЛЬС
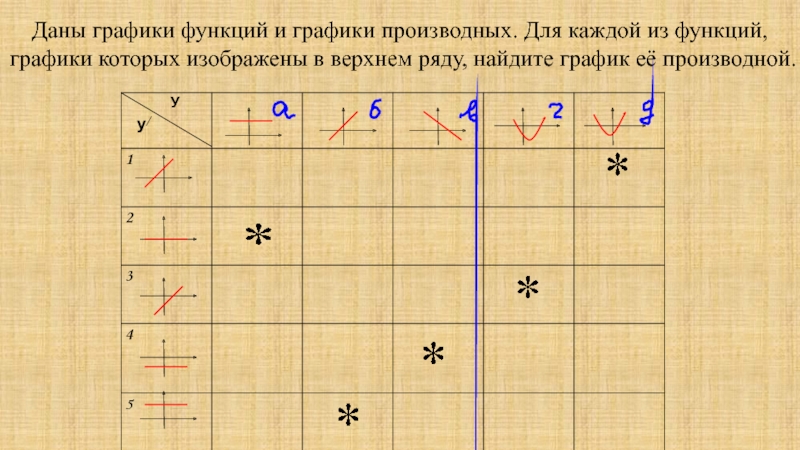
- 7. Даны графики функций и графики производных. Для
- 8. Найдите пары «функция – график производной этой функции»
- 9. Завершите фразы: «Если на отрезке [1; 3] производная …, то на этом отрезке функция у…
- 10. Готовимся к ЕГЭТРЕНАЖЁР по теме «ПРОИЗВОДНАЯ»Задание 7
- 11. 1) На рисунке изображен график функции у
- 12. 5118 2) Непрерывная функция у = f(x)
- 13. 3)На рисунке изображен график производной функции у
- 14. О1 2 3 4
- 15. -4 -3 -2
- 16. -4 -3 -2
- 17. 7) На рисунке изображен график производной функции.
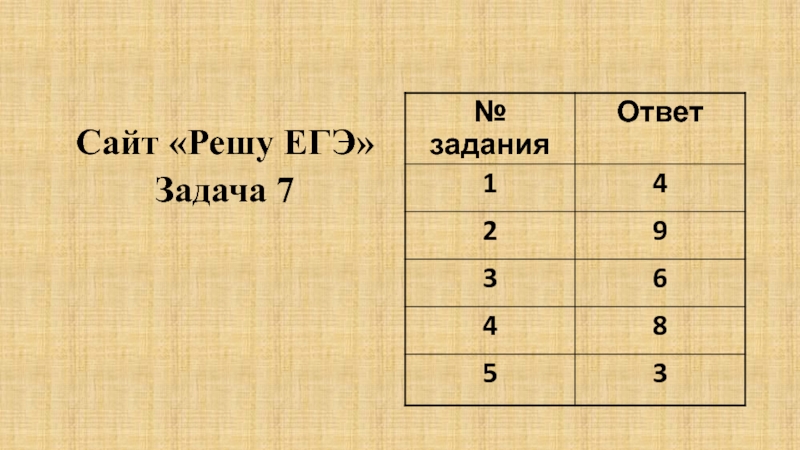
- 18. Сайт «Решу ЕГЭ»Задача 7
- 19. Физминутка
- 20. Алгоритм исследования функции на экстремумы:найти область определения
- 21. Алгоритм отыскания наибольшего и наименьшего значения функции
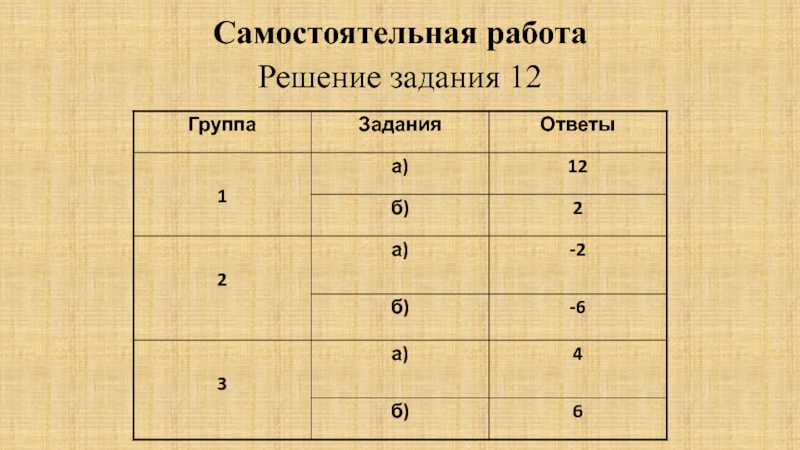
- 22. Самостоятельная работаРешение задания 12
- 23. Слайд 23
- 24. «Ум заключается не только в знании, но и в умении применять знания на практике»Аристотель
«Три пути ведут к знанию: путь размышления — это путь самый благородный, путь подражания — это путь самый легкий и путь опыта — это путь самый горький»Конфуций
Слайд 1МКОУ Докучаевская СОШ Мастер-класс по математике в 11 классе по теме: «ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
ФУНКЦИИ ПРИ РЕШЕНИИ ЗАДАЧ ЕГЭ»
Слайд 2«Три пути ведут к знанию: путь размышления — это путь самый благородный,
путь подражания — это путь самый легкий и путь опыта — это путь самый горький»
Конфуций
Конфуций
Слайд 4Алексей Николаевич Крылов (1863-1945)
«Человек обращается к математике не затем, чтобы любоваться
неисчислимыми сокровищами, ему прежде всего нужно ознакомиться со столетиями испытанными инструментами и научиться ими правильно и искусно владеть»
Слайд 5
-Зачем нужна производная?
-Где мы встречаемся с производной и используем её?
-Можно ли без производной обойтись в математике и не только?
Слайд 6«Лишь дифференциальное исчисление дает естествознанию
возможность изображать математически не только состояния,
но и процессы: движение»
Ф.ЭНГЕЛЬС
Ф.ЭНГЕЛЬС
Слайд 7Даны графики функций и графики производных. Для каждой из функций, графики
которых изображены в верхнем ряду, найдите график её производной.
![Завершите фразы: «Если на отрезке [1; 3] производная …, то на этом отрезке функция у…](/img/thumbs/8761206480ee3a70df02a8a3eb10cfce-800x.jpg "Мастер -класс Применение производной функции Завершите фразы: «Если на отрезке [1; 3] производная …, то на этом отрезке функция у…")
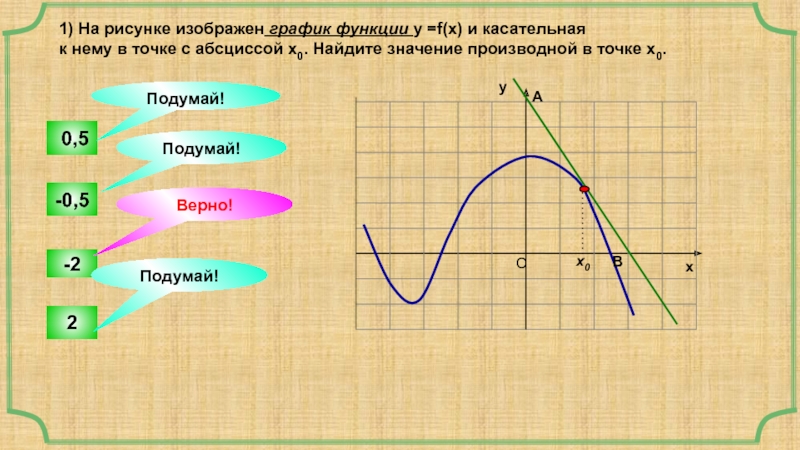
Слайд 111) На рисунке изображен график функции у =f(x) и касательная
к
нему в точке с абсциссой х0. Найдите значение производной в точке х0.
-2
-0,5
2
0,5
Подумай!
Подумай!
Верно!
Подумай!
х0
y
x
О
В
А
Слайд 125
11
8
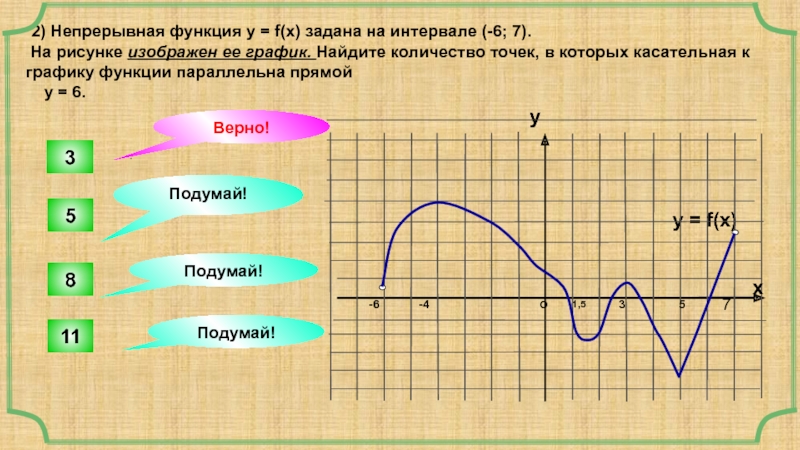
2) Непрерывная функция у = f(x) задана на интервале (-6;
7).
На рисунке изображен ее график. Найдите количество точек, в которых касательная к графику функции параллельна прямой
y = 6.
На рисунке изображен ее график. Найдите количество точек, в которых касательная к графику функции параллельна прямой
y = 6.
y = f(x)
y
x
3
Подумай!
Подумай!
Подумай!
Верно!
-6
7
.
О
-4
3
5
1,5
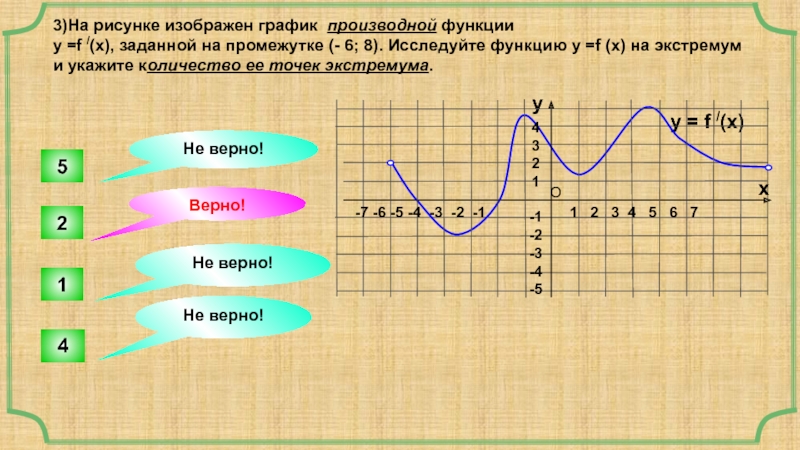
Слайд 133)На рисунке изображен график производной функции
у =f /(x), заданной на
промежутке (- 6; 8). Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек экстремума.
2
1
4
5
Не верно!
Не верно!
Верно!
Не верно!
y = f /(x)
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
О
Слайд 14О
1 2 3 4 5 х
4) На
рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите точку максимума функции.
1
4
-3
-1
Точка перегиба!
Точка минимума!
Верно!
Подумай!
y
-3
-1
Слайд 15 -4 -3 -2 -1
1 2
3 4 5 х
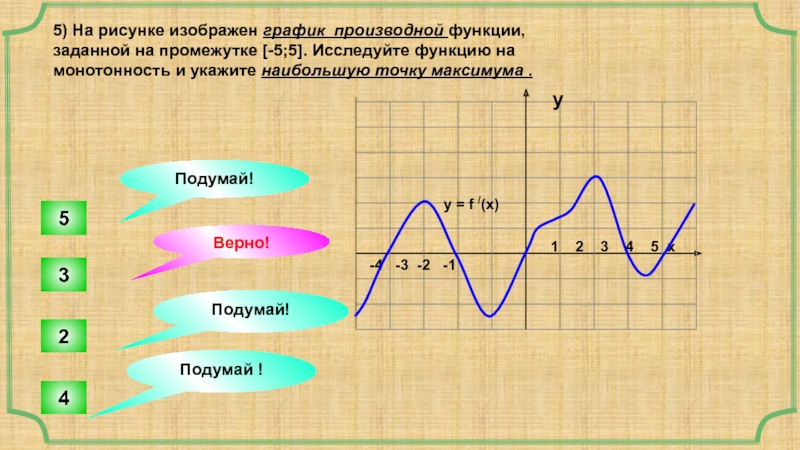
5) На рисунке изображен график производной функции,
заданной на промежутке [-5;5]. Исследуйте функцию на
монотонность и укажите наибольшую точку максимума .
3
2
4
5
Подумай!
Подумай !
Верно!
Подумай!
y = f /(x)
y
Слайд 16 -4 -3 -2 -1
1 2
3 4 5 х
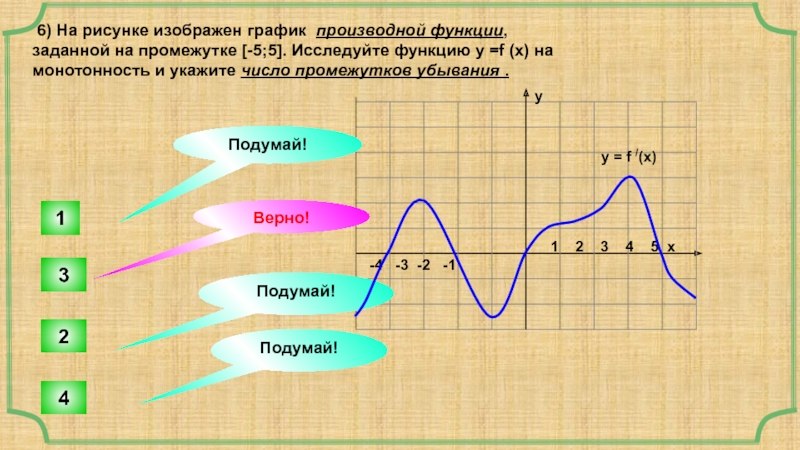
6) На рисунке изображен график производной функции,
заданной на промежутке [-5;5]. Исследуйте функцию у =f (x) на
монотонность и укажите число промежутков убывания .
3
2
4
1
Подумай!
Подумай!
Верно!
Подумай!
y = f /(x)
y
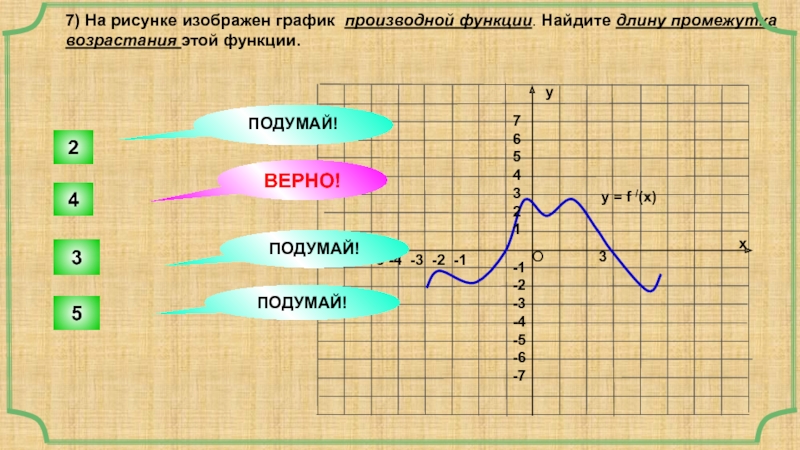
Слайд 177) На рисунке изображен график производной функции. Найдите длину промежутка возрастания
этой функции.
О
-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
4
2
3
5
ПОДУМАЙ!
ПОДУМАЙ!
ВЕРНО!
ПОДУМАЙ!
y
х
3
y = f /(x)
Слайд 20Алгоритм исследования функции на экстремумы:
найти область определения функции;
найти производную;
найти критические точки
функции;
отметить на координатной прямой все критические точки;
определить знак производной на каждом из полученных промежутков.
(Задание 12)
отметить на координатной прямой все критические точки;
определить знак производной на каждом из полученных промежутков.
(Задание 12)
Слайд 21Алгоритм отыскания наибольшего и наименьшего значения функции на отрезке:
найти область определения
функции;
найти производную;
найти критические точки и отобрать из них те, которые лежат внутри данного промежутка;
вычислить значения функции в отобранных точках и на концах отрезка;
выбрать из полученных значений наибольшее или наименьшее.
(Задание 12)
найти производную;
найти критические точки и отобрать из них те, которые лежат внутри данного промежутка;
вычислить значения функции в отобранных точках и на концах отрезка;
выбрать из полученных значений наибольшее или наименьшее.
(Задание 12)
Слайд 23 Домашнее задание
1. Продолжить работать с открытым банком
заданий ЕГЭ: решить все задания 7, 12 вариантов 1-5
(сайт «РЕШУ ЕГЭ»).
2. Решить задания 7,12 ЕГЭ 2019, математика профильная, Вариант1-10.
заданий ЕГЭ: решить все задания 7, 12 вариантов 1-5
(сайт «РЕШУ ЕГЭ»).
2. Решить задания 7,12 ЕГЭ 2019, математика профильная, Вариант1-10.
