- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Логарифмическая функция, её свойства и график
Содержание
- 1. Логарифмическая функция, её свойства и график
- 2. Определение. Логарифмом положительно числа b по положительному
- 3. Теорема об обратных функциях Если функция f(x)
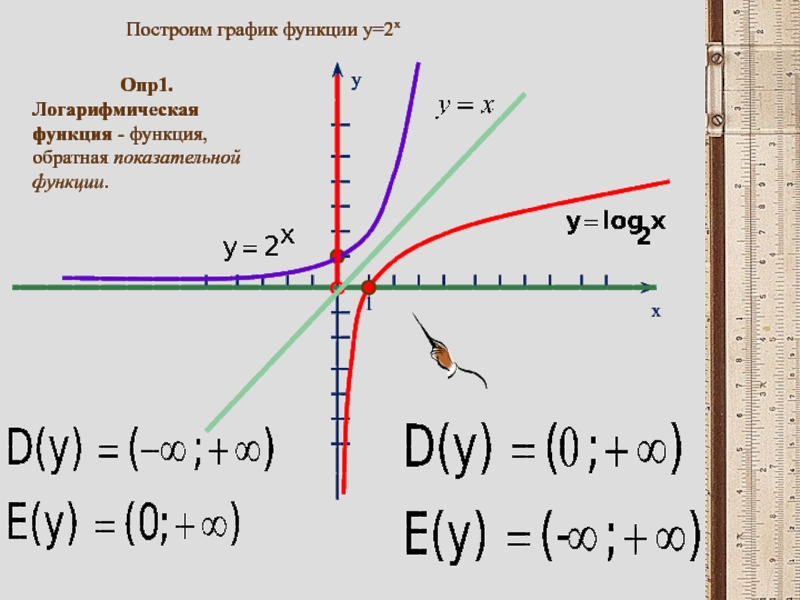
- 4. yx1Построим график функции y=2xОпр1.Логарифмическая функция - функция, обратная показательной функции.
- 5. yx1Построим график функции y=(0.5)x
- 6. Опр.2Функция вида y = loga х
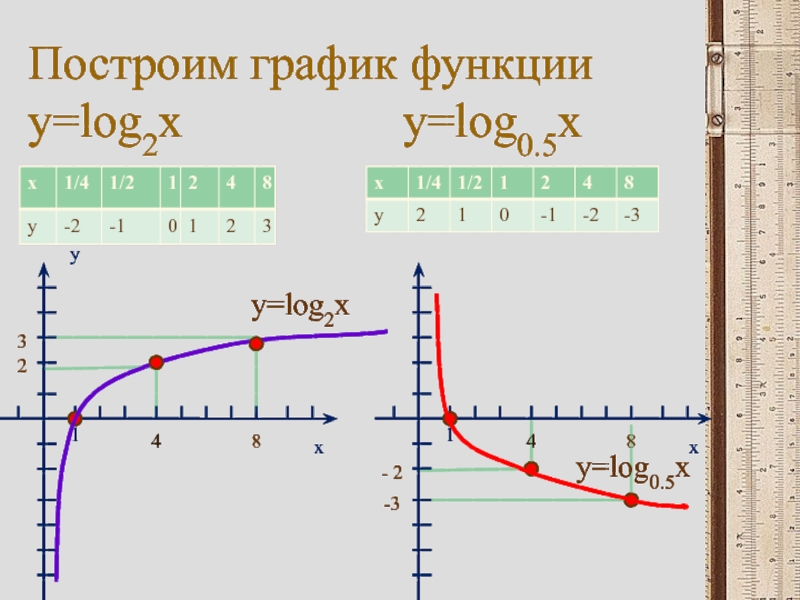
- 7. Построим график функции y=log2x
- 8. Свойства функцииСвойства функции y=loga x, при a>11)
- 9. Логарифмическая комедия математический софизм «2>3»
- 10. Работа в группах№1Найдите наибольшее и наименьшее значение
- 11. Найти наименьшее и набольшее значении функции на
- 12. Решить уравнения и неравенства а) lоg4x=0; б) lоg4x>0 в) lоg4x
- 13. y0 1 2 3
- 14. Решить уравнение lоg4x=5-xxy14Построим график функции y= lоg4xи
- 15. Построить графики функции функцииy=logxxD(y)=(0;1) (1;+∞) учитывая, что logaa=1, строим график y=1xy1
- 16. Построить графики функции функцииy=2log2xD(y)= (0;+∞) учитывая, что alogac=c, строим график y=xxy1
- 17. Построить графики функции функцииy=xlogx2D(y)=(0;1) (1;+∞) учитывая, что
- 18. Применение логарифмов в физике, химии, биологии
- 19. Физики шутят: “ Математика – царица всех
- 20. Преобразование графиков функцииxy1 2 3
- 21. Преобразование графиков функцииxy1 2 3
- 22. Преобразование графиков функцииxy1 2 3
- 23. Известно завещание знаменитого американского государственного деятеля
- 24. Вычисления с помощью логарифма
- 25. Используемая литература:Задача на 2 слайде:http://www.bankrabot.com/part2/work_12766.htmlУчебник: Мордкович А.Г.,
Слайд 2Определение.
Логарифмом положительно числа b по положительному и отличному от 1
Слайд 3Теорема об обратных функциях
Если функция f(x) определена и
монотонна на
причем D(f)=X,
E(f)=Y, то
существует обратная ей функция g(x), определенная на Y, т.е. D(g)=Y
E(g)=X,
причем, монотонность сохраняется. Графики взаимнообратных функций симметричны относительно прямой y=x
Слайд 4y
x
1
Построим график функции y=2x
Опр1.
Логарифмическая функция - функция, обратная показательной функции.
Слайд 6Опр.2
Функция вида y = loga х
(где а > 0,
1) D(y):(0;+∞) Это следует из определения логарифма, так как выражение logax имеет смысл только при x > 0.
Устная работа
Найти D(y), если известно, что а > 0, а ≠ 1
а) y = loga х +1
б) y = loga (х+1)
в) y = loga (1-x)
Слайд 8Свойства функции
Свойства функции y=loga x, при a>1
1) D(F):(0;+∞)
2) не является ни
3) возрастает на своей области определения
4) не ограничена ни сверху, ни снизу
5) не имеет ни наибольшего, ни наименьшего значений
6) непрерывна
7) E(F):(- ∞;+ ∞)
8) выпукла вверх
x y y=logax a>1 y=logax 0 Устно
Свойства функции y=loga x, при 0
2) не является ни четной, ни нечетной
3) убывает на своей области определения
4) не ограничена ни сверху, ни снизу
5) не имеет ни наибольшего, ни наименьшего значений
6) непрерывна
7) E(F):(- ∞;+ ∞)
8) выпукла вниз
Выполняем задание 15.12
Слайд 10Работа в группах
№1Найдите наибольшее и наименьшее значение функции на заданном промежутке
№2 Решите уравнение и неравенства
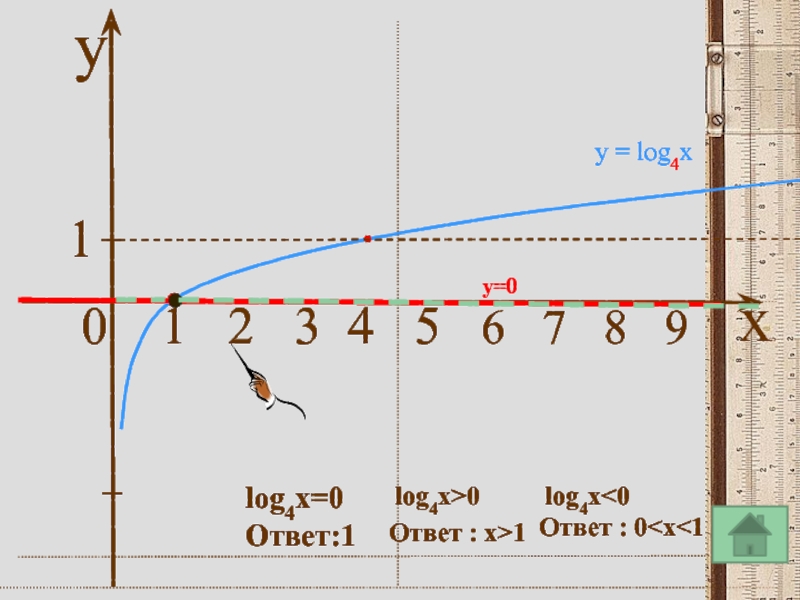
а) lоg4x=0; б) lоg4x>0 в) lоg4x<0
№3 Решите уравнение lоg4x=5-x
№4 Постройте графики функций а)y=logxx
б) y=2log2x в) y=xlogx2
подсказка
подсказка
подсказка
подсказка
подсказка
подсказка
Слайд 11Найти наименьшее и набольшее значении функции на заданном промежутке
y=lgx x€ [1;1000]
Решение:
Следовательно своего наименьшего и наибольшего значения достигает на концах отрезка
yнаим=lg1=0
yнаиб=lg1000=3
Слайд 12Решить уравнения и неравенства а) lоg4x=0; б) lоg4x>0 в) lоg4x
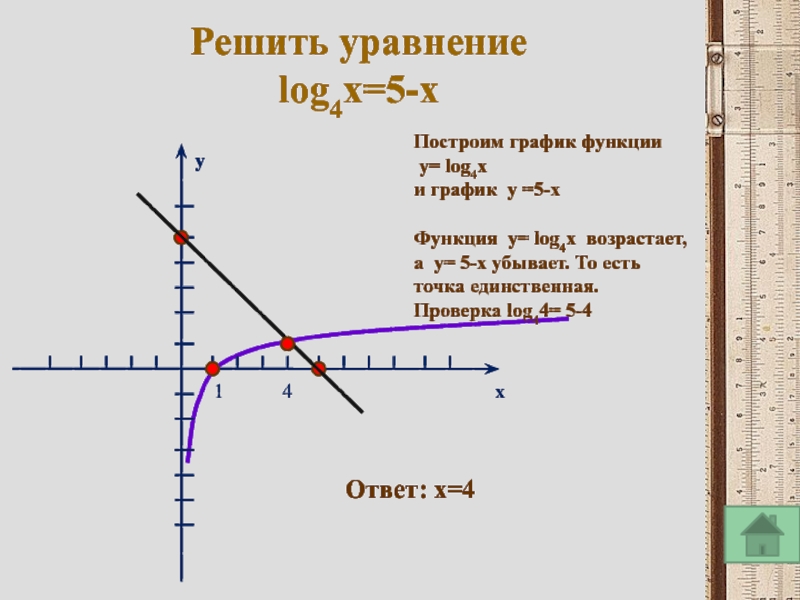
Слайд 14Решить уравнение
lоg4x=5-x
x
y
1
4
Построим график функции
y= lоg4x
и график y =5-x
Функция y=
а y= 5-x убывает. То есть точка единственная.
Проверка lоg44= 5-4
Ответ: x=4
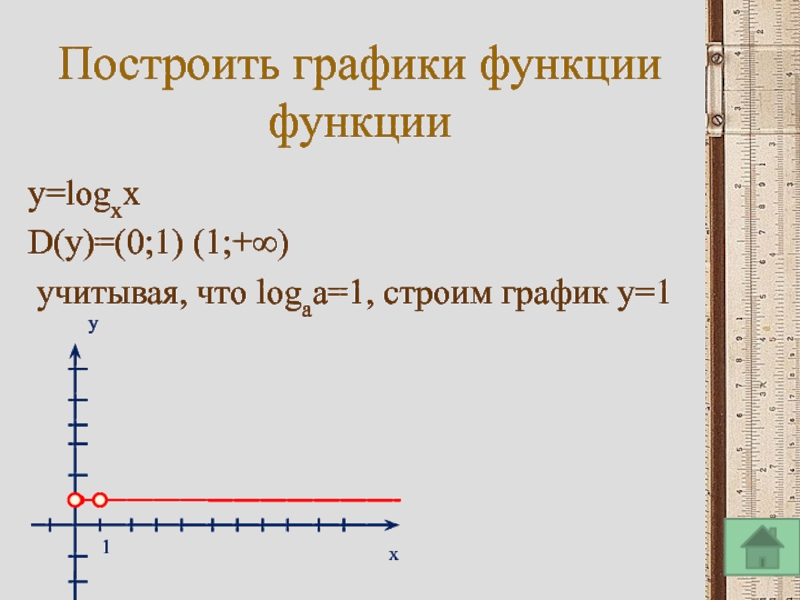
Слайд 15Построить графики функции
функции
y=logxx
D(y)=(0;1) (1;+∞)
учитывая, что logaa=1, строим график y=1
x
y
1
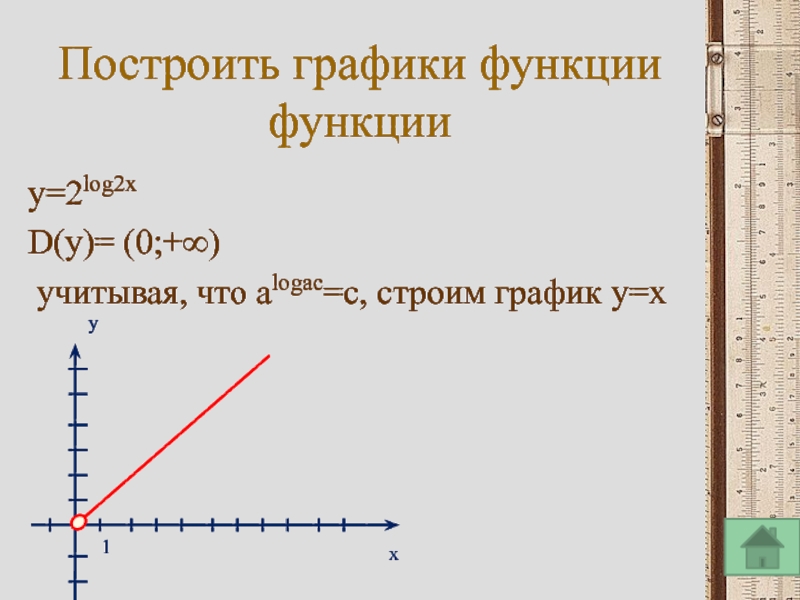
Слайд 16Построить графики функции
функции
y=2log2x
D(y)= (0;+∞)
учитывая, что alogac=c, строим график y=x
x
y
1
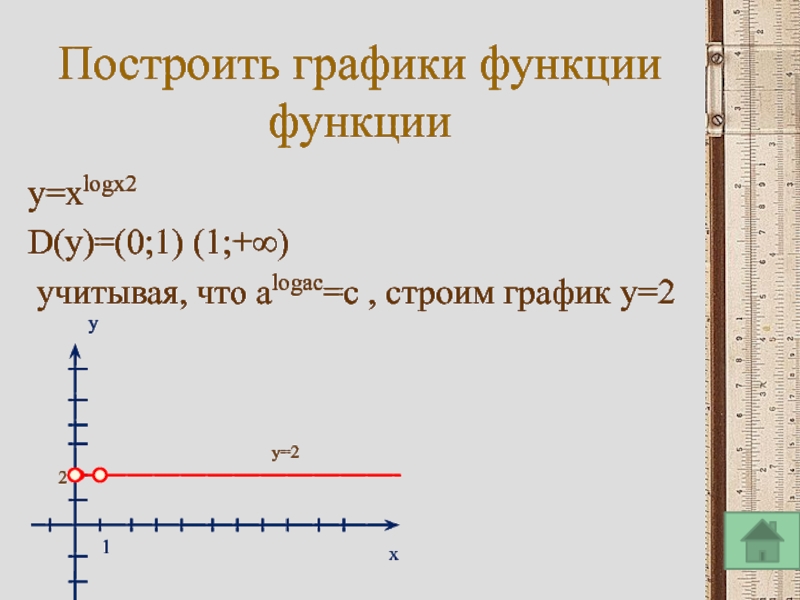
Слайд 17Построить графики функции
функции
y=xlogx2
D(y)=(0;1) (1;+∞)
учитывая, что alogac=c , строим график y=2
y=2
2
x
y
1
Слайд 19Физики шутят: “ Математика – царица всех наук, но служанка физики”.
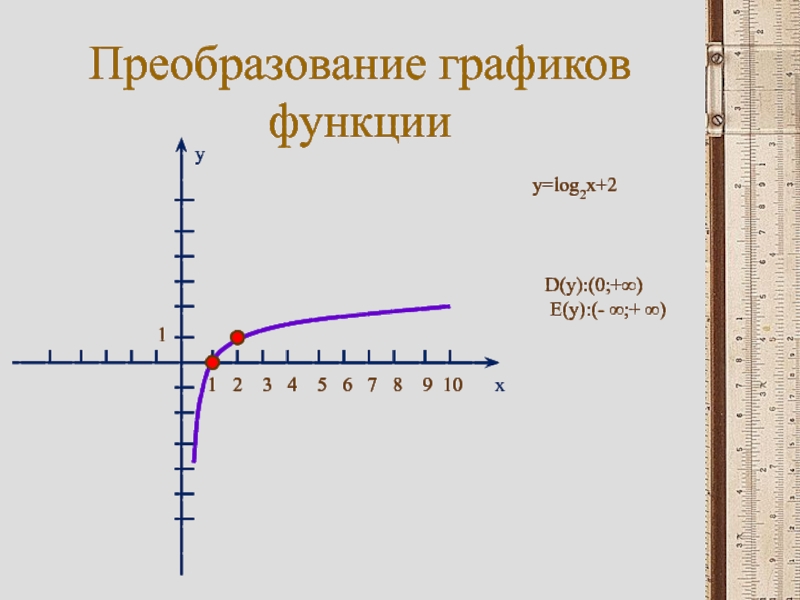
Слайд 21Преобразование графиков функции
x
y
1 2 3 4 5
1
y=log2(x+2)
D(y):(-2;+∞)
E(y):(- ∞;+ ∞)
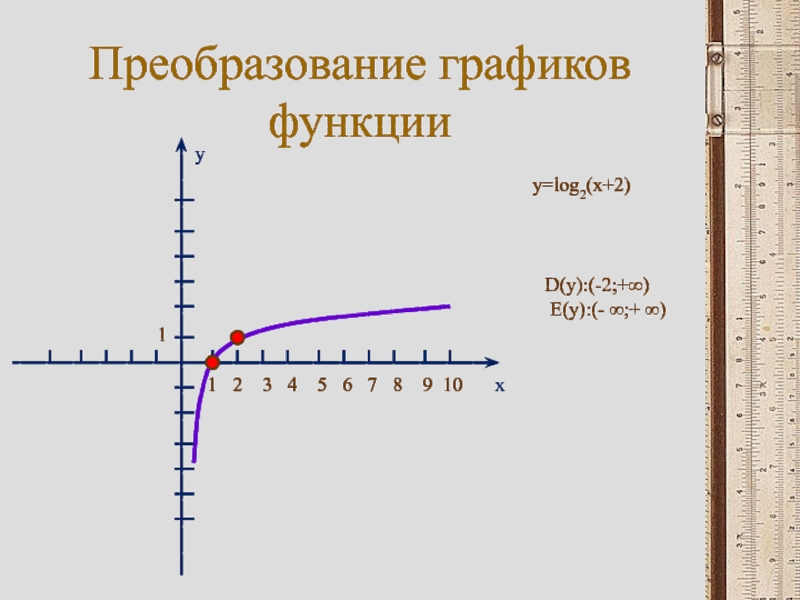
Слайд 22Преобразование графиков функции
x
y
1 2 3 4 5
1
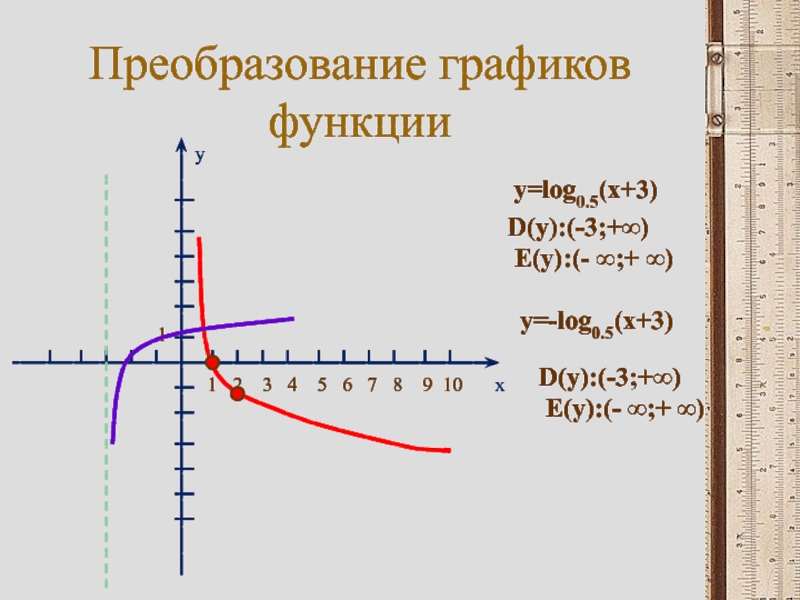
y=log0.5(x+3)
D(y):(-3;+∞)
E(y):(- ∞;+ ∞)
y=-log0.5(x+3)
D(y):(-3;+∞)
E(y):(- ∞;+ ∞)
Слайд 23 Известно завещание знаменитого американского государственного деятеля Бенджамина Франклина. Вот отрывок
Слайд 25Используемая литература:
Задача на 2 слайде:http://www.bankrabot.com/part2/work_12766.html
Учебник: Мордкович А.Г., «Алгебра и начала анализа»,
Задачник: Мордкович А.Г., «Алгебра и начала анализа», профильный уровень
http://www.matica.info/material1.html -завещание Франклина.







![Логарифмическая функция, её свойства и график Работа в группах№1Найдите наибольшее и наименьшее значение функции на заданном промежутке Работа в группах№1Найдите наибольшее и наименьшее значение функции на заданном промежутке y=lgx x€ [1;1000]№2 Решите уравнение и](/img/thumbs/8972f563d7bb12c19060e6666708e02a-800x.jpg)
![Логарифмическая функция, её свойства и график Найти наименьшее и набольшее значении функции на заданном промежуткеy=lgx x€ [1;1000]Решение: Найти наименьшее и набольшее значении функции на заданном промежуткеy=lgx x€ [1;1000]Решение: функция y=lgx непрерывная и возрастающая.Следовательно своего](/img/thumbs/b429f219839e579021fe218e4002eadb-800x.jpg)