- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Квадратичная функция в 8 класс
Содержание
- 1. Квадратичная функция в 8 класс
- 2. Страница 1. «Функция – одна из основных
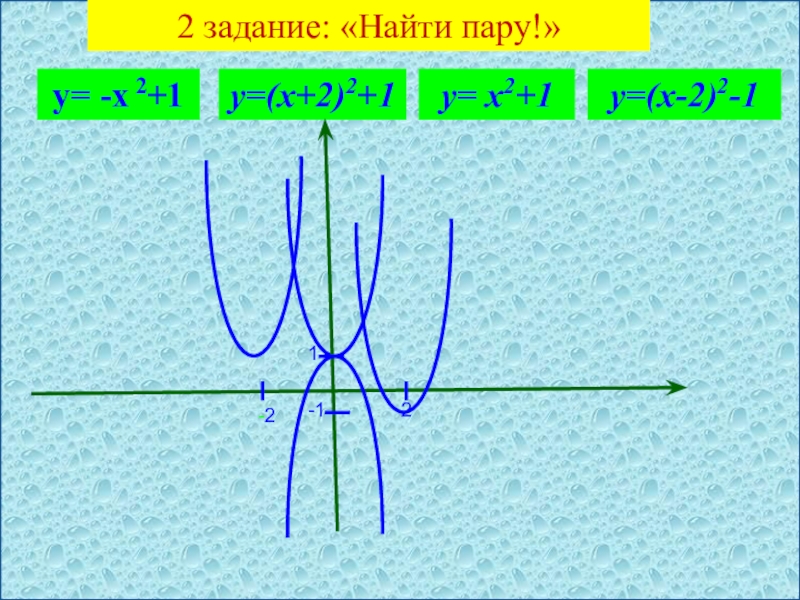
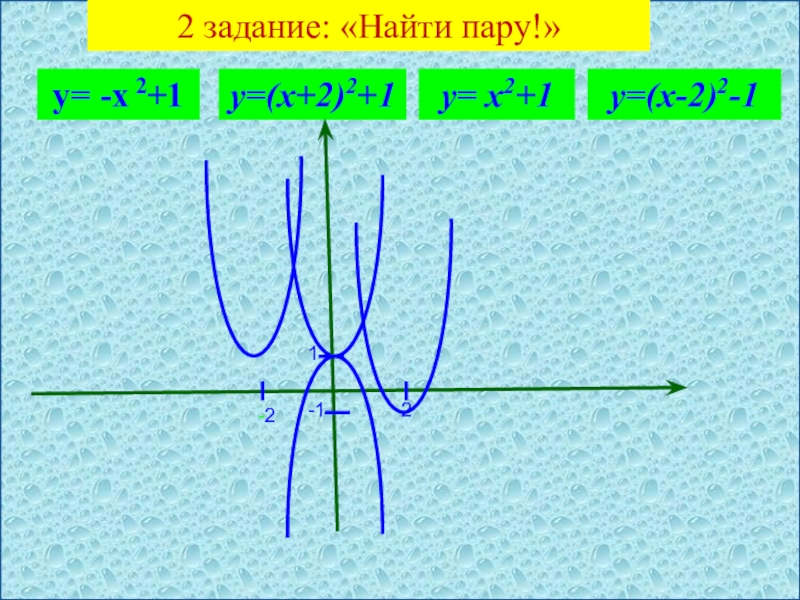
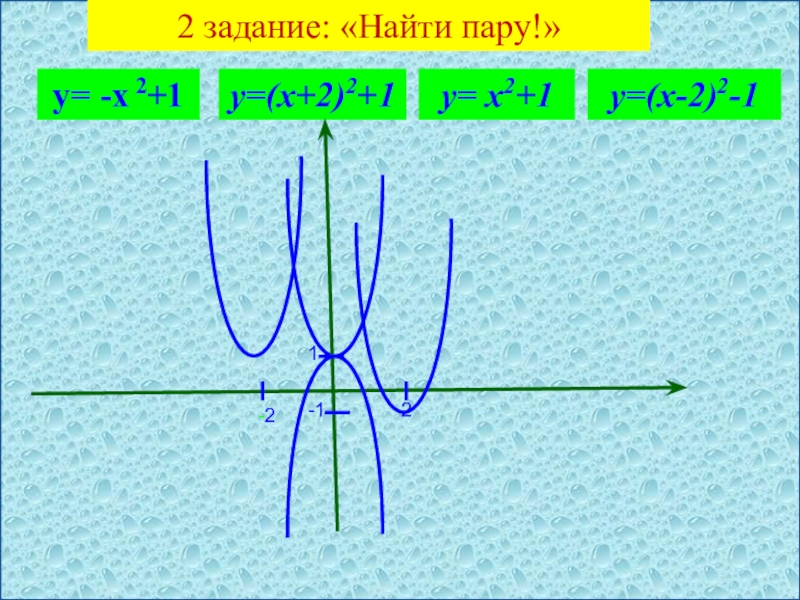
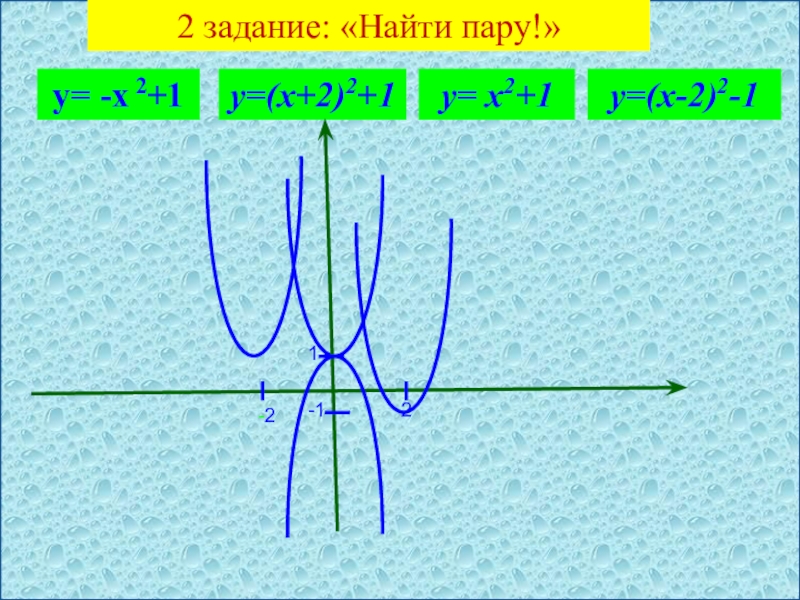
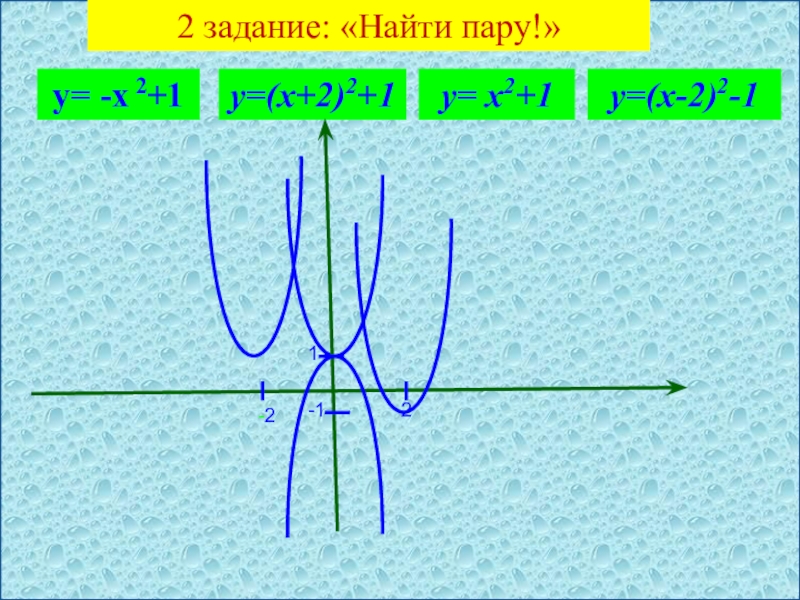
- 3. 2 задание: «Найти пару!» у= -х 2+1у= х2+1у=(х+2)2+1у=(х-2)2-12-21-1
- 4. Исторические тайны Функция по-латински означает –
- 5. 2 задание: «Найти пару!» у= -х 2+1у= х2+1у=(х+2)2+1у=(х-2)2-12-21-1
- 6. 2 задание: «Найти пару!» у= -х 2+1у= х2+1у=(х+2)2+1у=(х-2)2-12-21-1
- 7. 2 задание: «Найти пару!» у= -х 2+1у= х2+1у=(х+2)2+1у=(х-2)2-12-21-1
- 8. 2 задание: «Найти пару!» у= -х 2+1у= х2+1у=(х+2)2+1у=(х-2)2-12-21-1
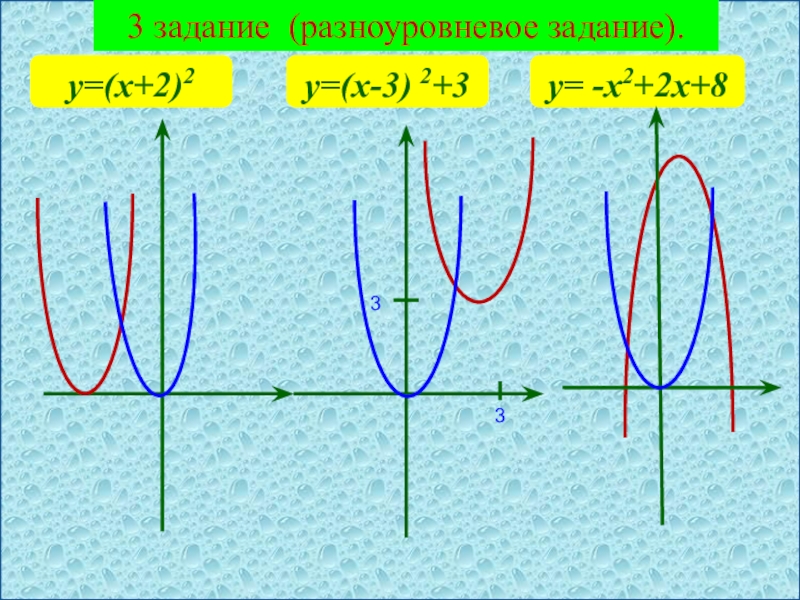
- 9. 3 задание (разноуровневое задание). у=(х+2)2у= -х2+2х+8у=(х-3) 2+33 3
- 10. Парабола по–гречески дополнительно. Прямой конус не проходит
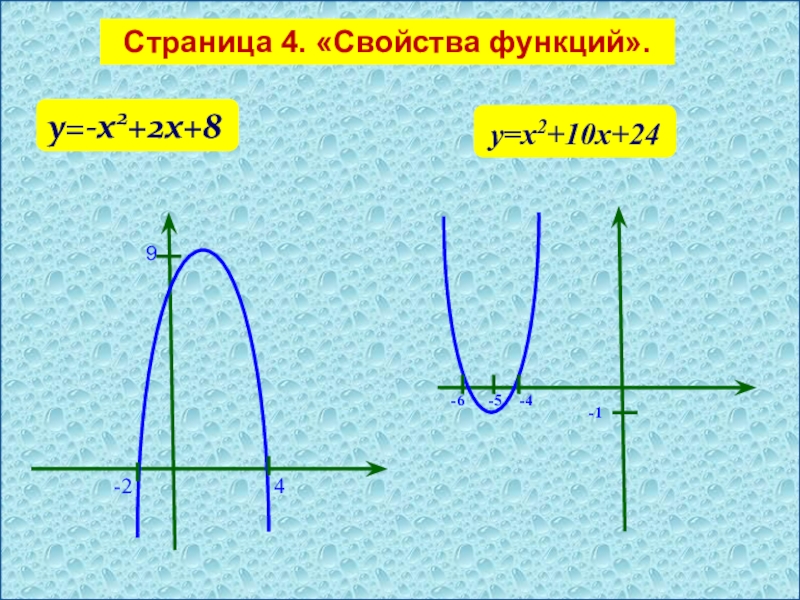
- 11. Страница 4. «Свойства функций». у=-х2+2х+8 у=х2+10х+24 4-29-5-4-6-1
- 12. Страница 5. «Проверь свои знания!» Задача 1: В каком
- 13. Страница 5. «Проверь свои знания!» Задача 1: В каком
Страница 1. «Функция – одна из основных математических понятии»;Страница 2. «График функции-множество точек координатных плоскостей»;Страница 3. «Парабола-график квадратичной функций»;Страница 4. «Своиства функций»;Страница 5. «Проверь свой знания!»
Слайд 2
Страница 1. «Функция – одна из
основных математических понятии»;
Страница 2. «График
функции-множество точек координатных плоскостей»;
Страница 3. «Парабола-график квадратичной функций»;
Страница 4. «Своиства функций»;
Страница 5. «Проверь свой знания!»
Страница 3. «Парабола-график квадратичной функций»;
Страница 4. «Своиства функций»;
Страница 5. «Проверь свой знания!»
Слайд 4
Исторические тайны
Функция по-латински означает – выполнение.
В 1692г. немецкий
математик Готфрид Лейбниц
(1646-1716) останавивался в своих работах о
роли функции, а в 1718 г. швейцарский
математик Иоганн Бернулли (1667-1748)
отметил, что функция – математическое
понятие, выражающее переменную через другую.
.
Шуточных вопросы: В течение 12 месяцев
меняются 30 и 31 число, а в каком месяце
встрается 28 число?
(1646-1716) останавивался в своих работах о
роли функции, а в 1718 г. швейцарский
математик Иоганн Бернулли (1667-1748)
отметил, что функция – математическое
понятие, выражающее переменную через другую.
.
Шуточных вопросы: В течение 12 месяцев
меняются 30 и 31 число, а в каком месяце
встрается 28 число?
Слайд 10
Парабола по–гречески дополнительно. Прямой конус не проходит через вершину и линию,
которая образуется при пересечении плоскости и касательной. В 200 г. до н. э. Апполлонии впервые ввёл научное название парабола.
Задача. Верх стола четырехугольный, если отрезать один угол, то сколько углов остается?
Задача. Верх стола четырехугольный, если отрезать один угол, то сколько углов остается?
Исторические тайны
Слайд 12
Страница 5. «Проверь свои знания!»
Задача 1:
В каком значении а, ось симметрии
параболы у=ах2-16х+1 является прямой: х=4
Задача 2:
В каком значении в и с, если вершина параболы у=х2-6х+с является (6; -12)?
Задача 3:
Найти значения а и в в точках М(1;2) и N(2;10) в графике функции у=ах2+вх-18.
Задача 2:
В каком значении в и с, если вершина параболы у=х2-6х+с является (6; -12)?
Задача 3:
Найти значения а и в в точках М(1;2) и N(2;10) в графике функции у=ах2+вх-18.
Слайд 13
Страница 5. «Проверь свои знания!»
Задача 1:
В каком значении а, ось симметрии
параболы у=ах2-16х+1 является прямой: х=4
Задача 2:
В каком значении в и с, если вершина параболы у=х2-6х+с является (6; -12)?
Задача 3:
Найти значения а и в в точках М(1;2) и N(2;10) в графике функции у=ах2+вх-18.
Задача 2:
В каком значении в и с, если вершина параболы у=х2-6х+с является (6; -12)?
Задача 3:
Найти значения а и в в точках М(1;2) и N(2;10) в графике функции у=ах2+вх-18.