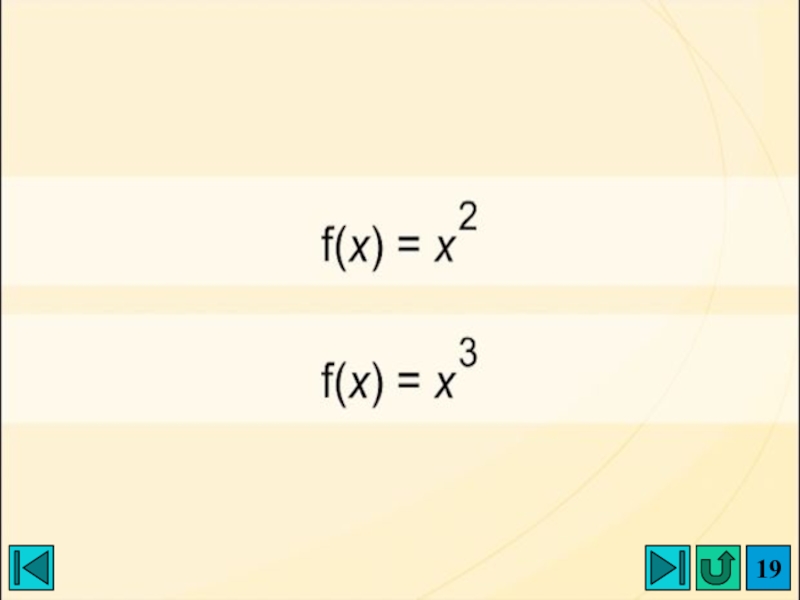функции
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему КРИТИЧЕСКИЕ ТОЧКИ И ЭКСТРЕМУМЫ ФУНКЦИИ
Содержание
- 1. КРИТИЧЕСКИЕ ТОЧКИ И ЭКСТРЕМУМЫ ФУНКЦИИ
- 2. Найти значения х, при которых значение f(x) равно 0
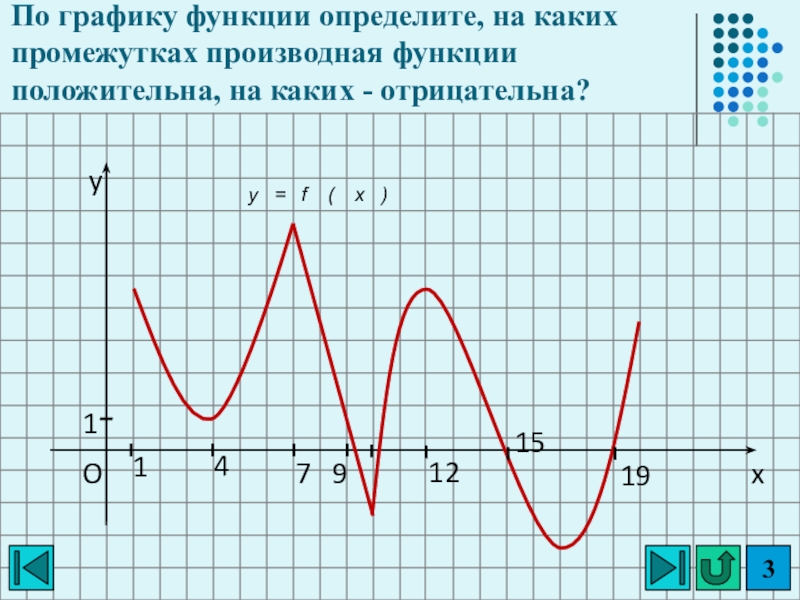
- 3. xyO11479121519По графику функции определите, на каких промежутках производная функции положительна, на каких - отрицательна?
- 4. y = f ´(х) По графику производной
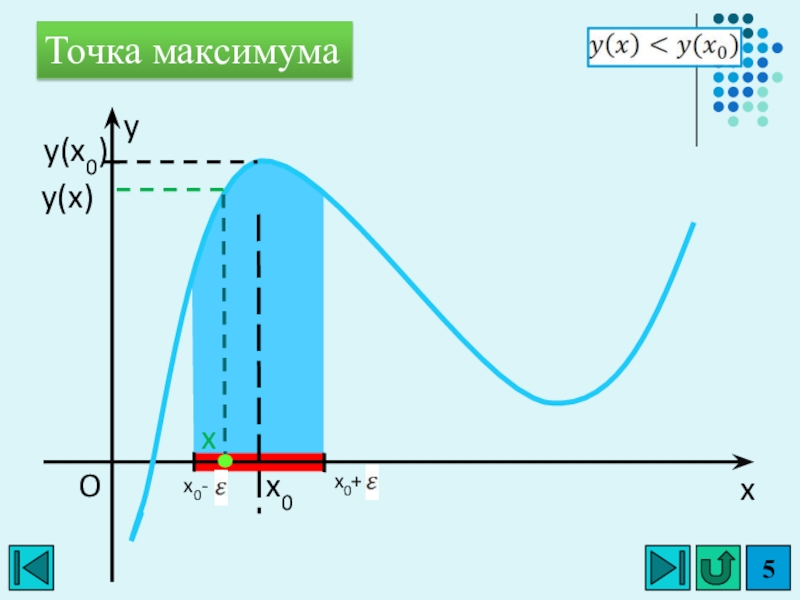
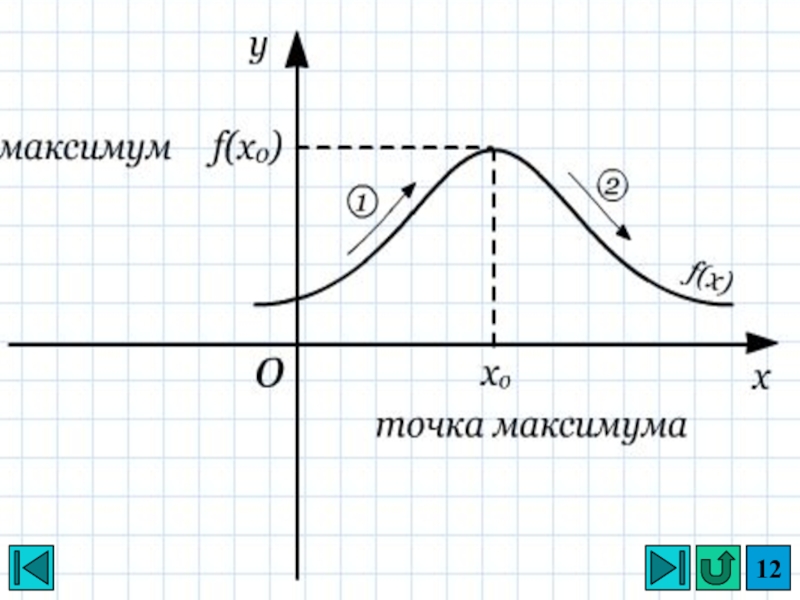
- 5. xyOx0Точка максимумаx0+x0-xy(x0)y(x)
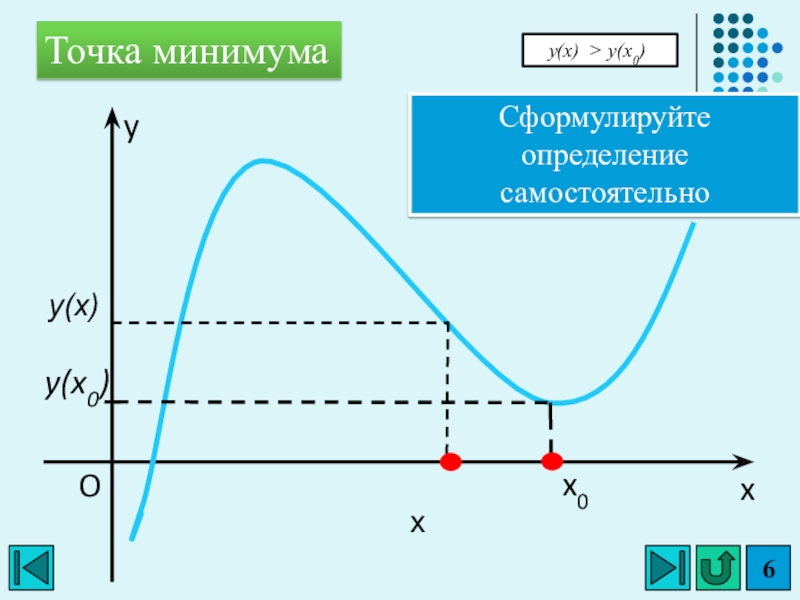
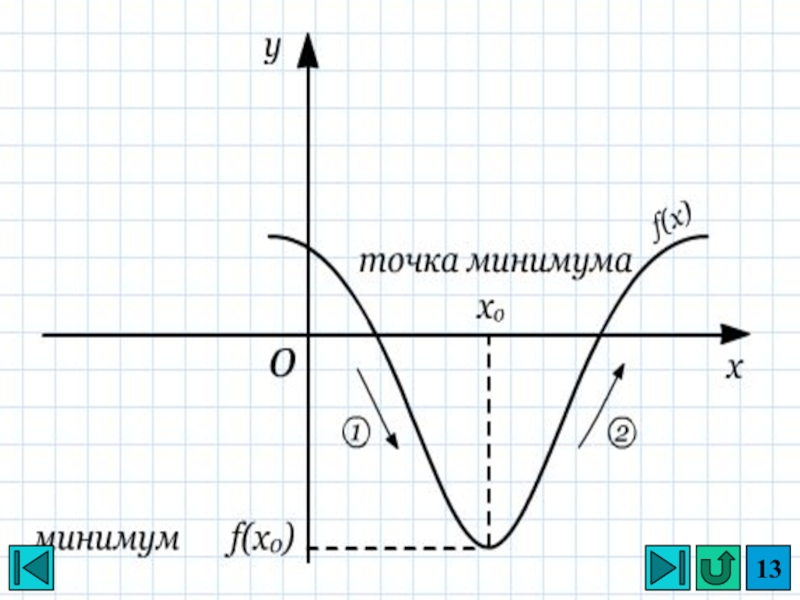
- 6. xOx0Точка минимумаy(x0)yСформулируйте определение самостоятельноy(х) > y(x0)
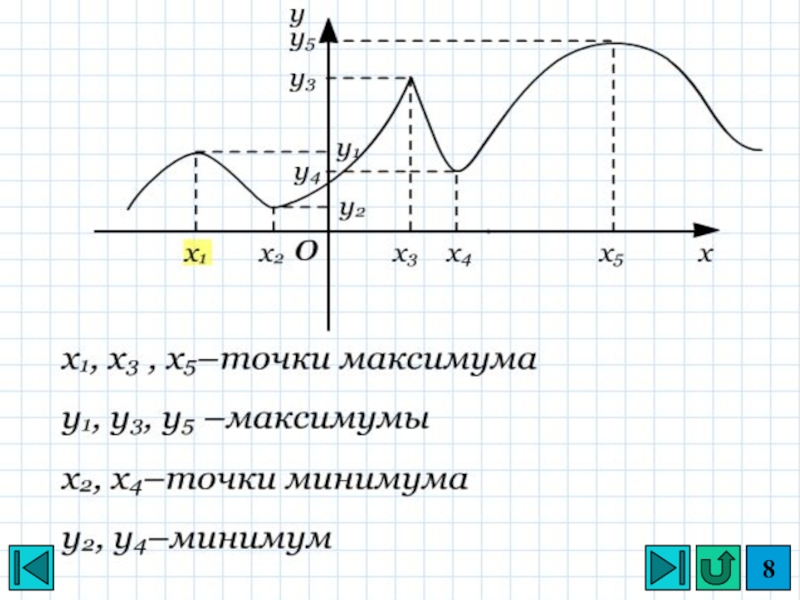
- 7. Точки максимума и минимума называются точками экстремума функции
- 8. Слайд 8
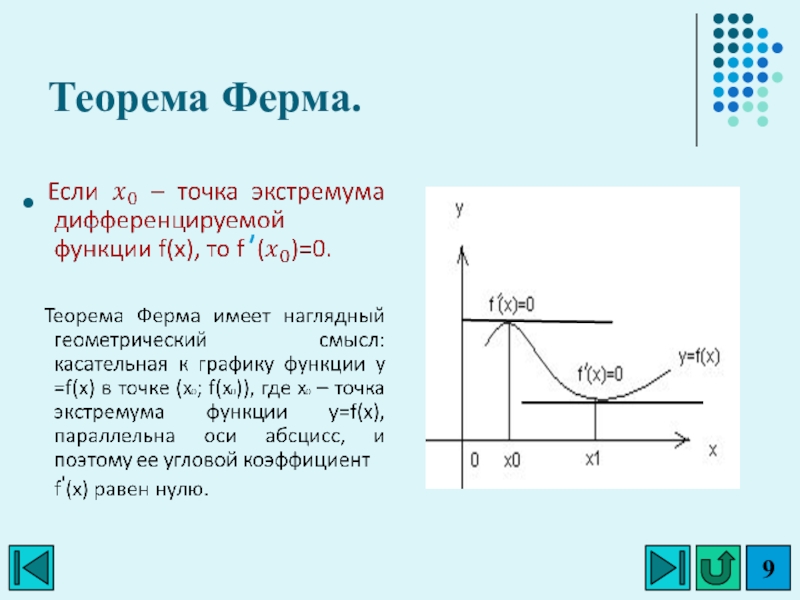
- 9. Теорема Ферма.
- 10. Внутренние точки области определения функции,
- 11. Для того, чтобы точка была точкой экстремума
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Необходимое и достаточное условие экстремума. Для того
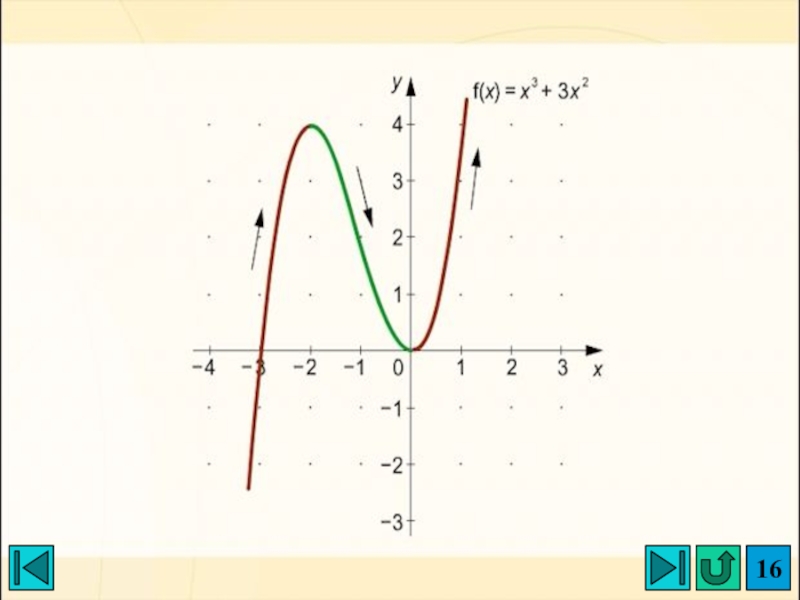
- 16. Слайд 16
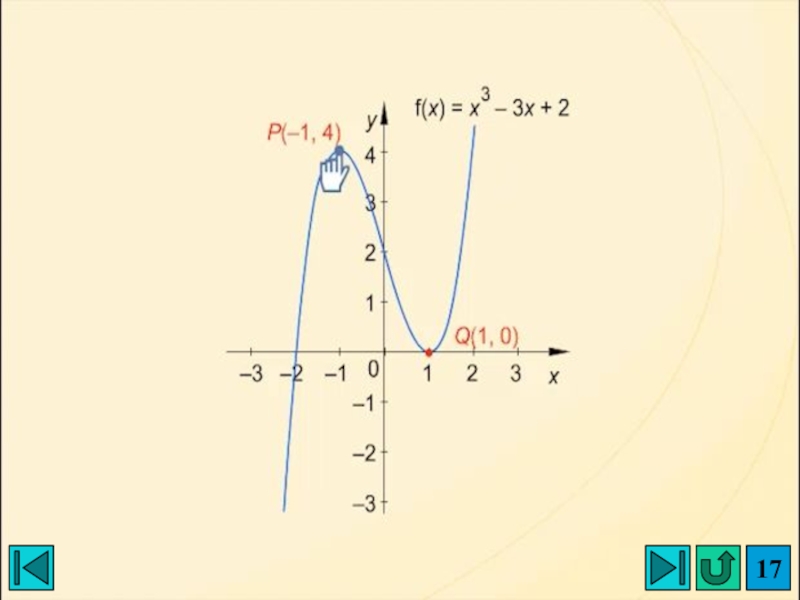
- 17. Слайд 17
- 18. Алгоритм нахождения точек экстремума: Найти производную функции.Решить
- 19. Слайд 19
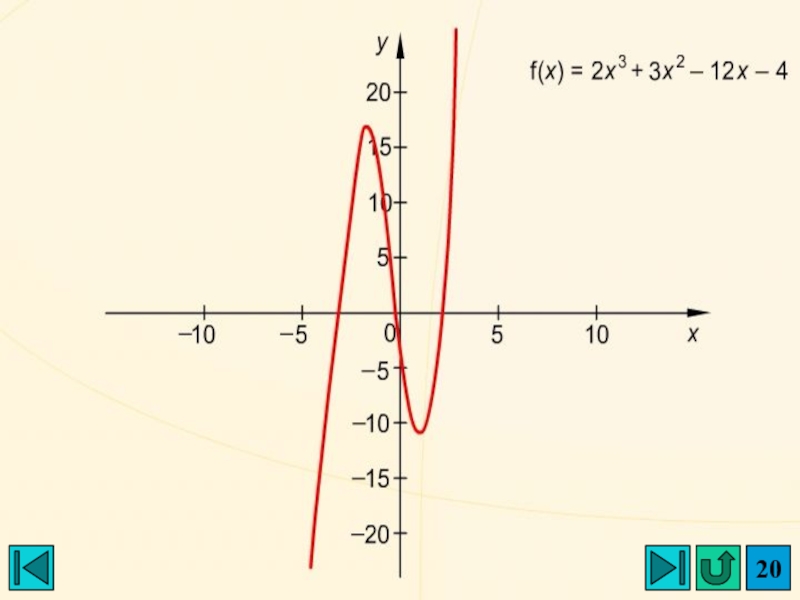
- 20. Слайд 20
Найти значения х, при которых значение f(x) равно 0
Слайд 3x
y
O
1
1
4
7
9
12
15
19
По графику функции определите, на каких промежутках производная функции положительна, на
каких - отрицательна?
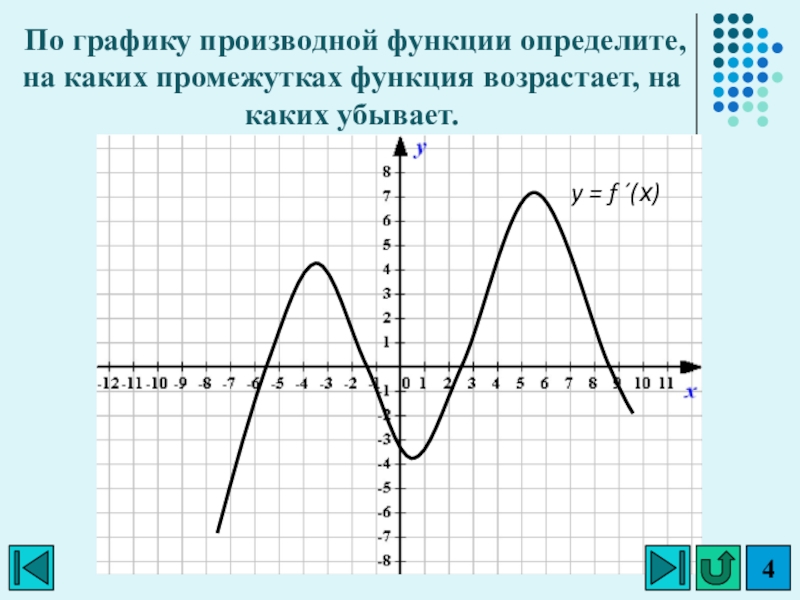
Слайд 4y = f ´(х)
По графику производной функции определите, на каких
промежутках функция возрастает, на каких убывает.
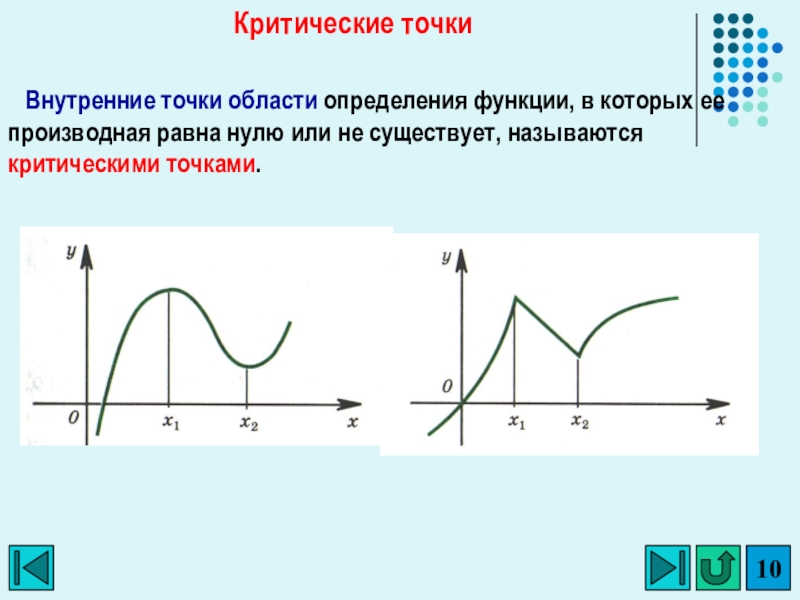
Слайд 10 Внутренние точки области определения функции, в которых ее производная
равна нулю или не существует, называются критическими точками.
Критические точки
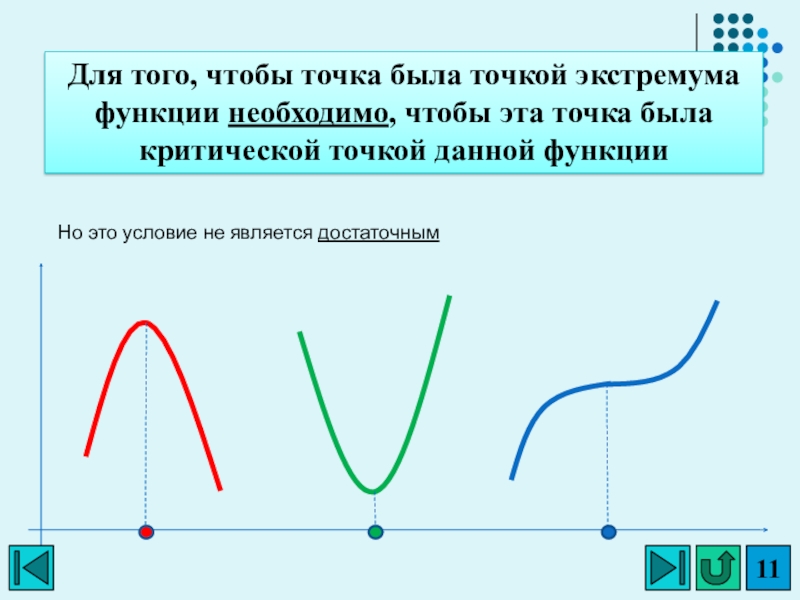
Слайд 11Для того, чтобы точка была точкой экстремума функции необходимо, чтобы эта
точка была критической точкой данной функции
Но это условие не является достаточным
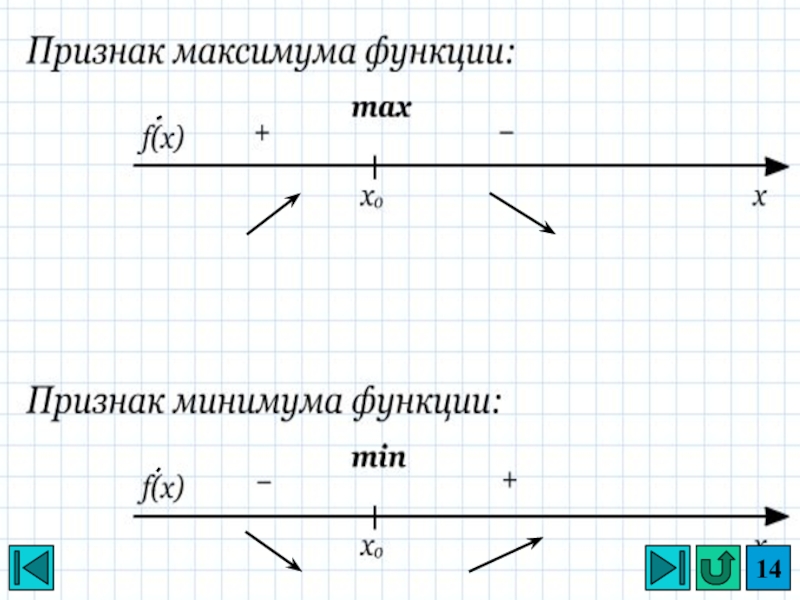
Слайд 15Необходимое и достаточное условие экстремума.
Для того , чтобы точка х0
была точкой экстремума функции f(х):
необходимо , чтобы х0 была критической точкой функции;
достаточно, чтобы при переходе через критическую точку х0 производная меняла знак.
необходимо , чтобы х0 была критической точкой функции;
достаточно, чтобы при переходе через критическую точку х0 производная меняла знак.
Слайд 18Алгоритм нахождения точек экстремума:
Найти производную функции.
Решить уравнение f ´(х)=0, и
найти тем самым стационарные точки.
Методом интервалов установить промежутки знакопостоянства производной.
Если при переходе через точку х0:
- производная не меняет знак, то х0 – точка перегиба;
- производная меняет знак с «+» на «-», то х0 точка максимума;
- производная меняет знак с «-» на «+», то х0 точка минимума.
Методом интервалов установить промежутки знакопостоянства производной.
Если при переходе через точку х0:
- производная не меняет знак, то х0 – точка перегиба;
- производная меняет знак с «+» на «-», то х0 точка максимума;
- производная меняет знак с «-» на «+», то х0 точка минимума.