это то, чего можно добиться»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Координатный метод решения задач 11 класс
Содержание
- 1. Координатный метод решения задач 11 класс
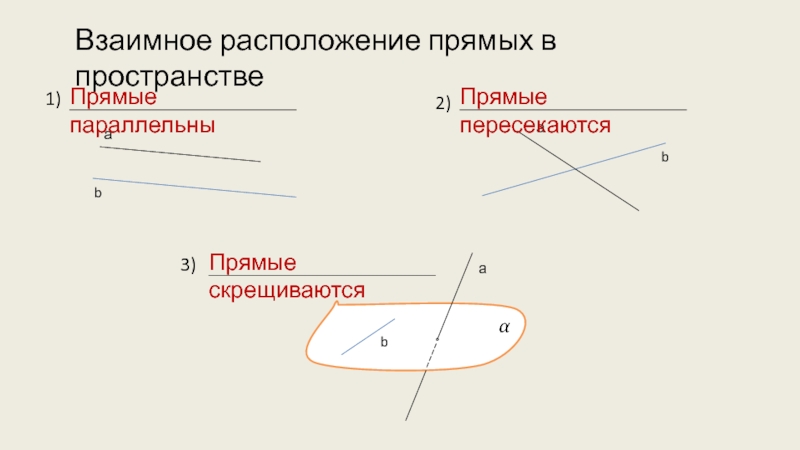
- 2. Взаимное расположение прямых в пространстве 1)2)3)аbаbbаПрямые параллельныПрямые пересекаютсяПрямые скрещиваются
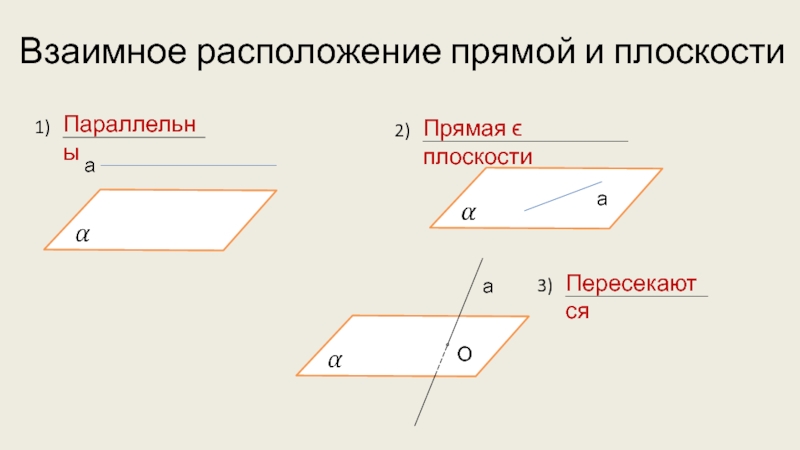
- 3. Взаимное расположение прямой и плоскости1)а2)а3)аОПараллельныПрямая ϵ плоскостиПересекаются
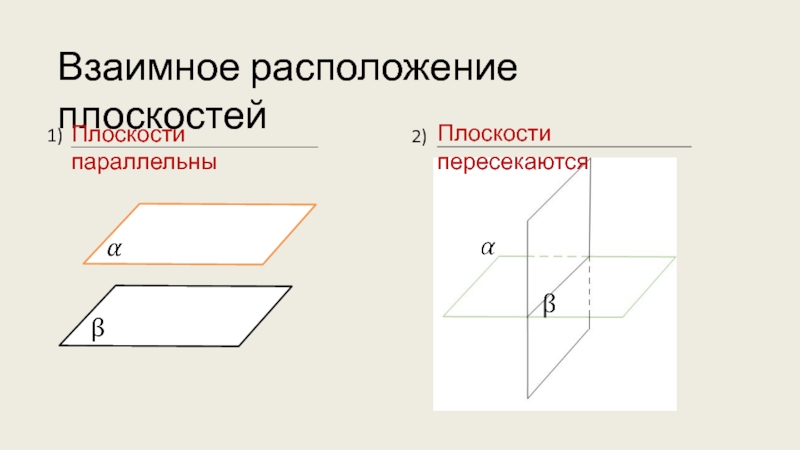
- 4. Взаимное расположение плоскостей1)2)Плоскости параллельныПлоскости пересекаются
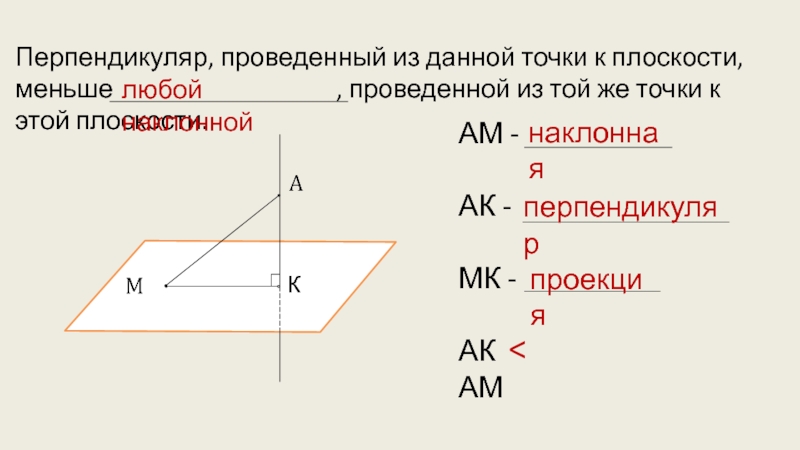
- 5. Перпендикуляр, проведенный из данной точки к плоскости,
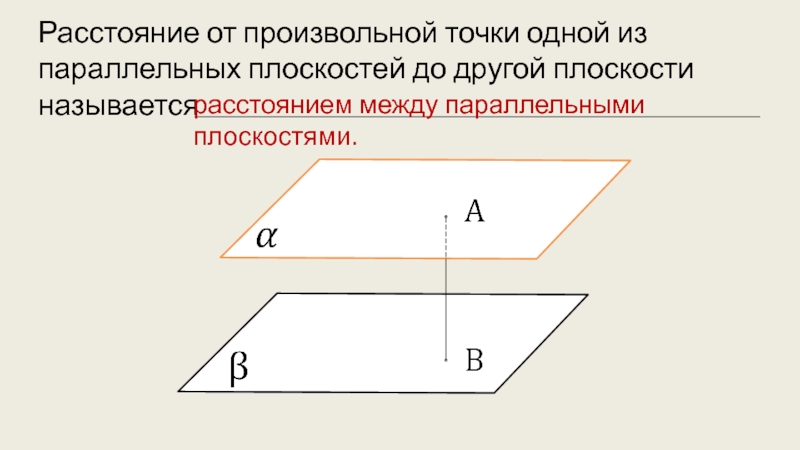
- 6. Расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости называетсярасстоянием между параллельными плоскостями.
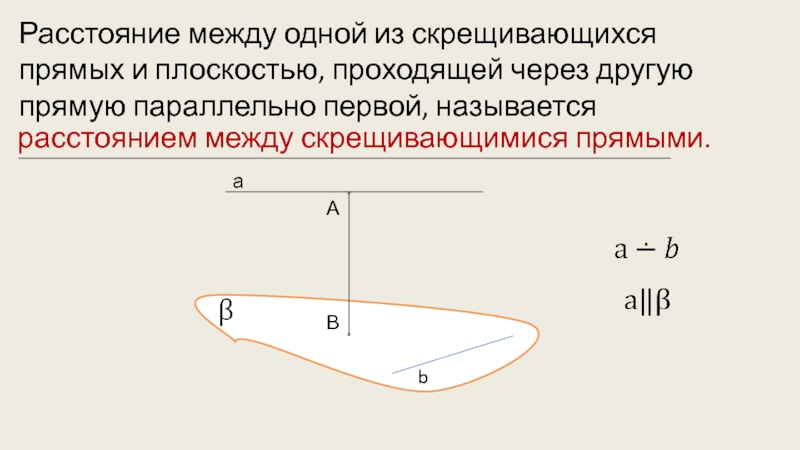
- 7. Расстояние между одной из скрещивающихся прямых и
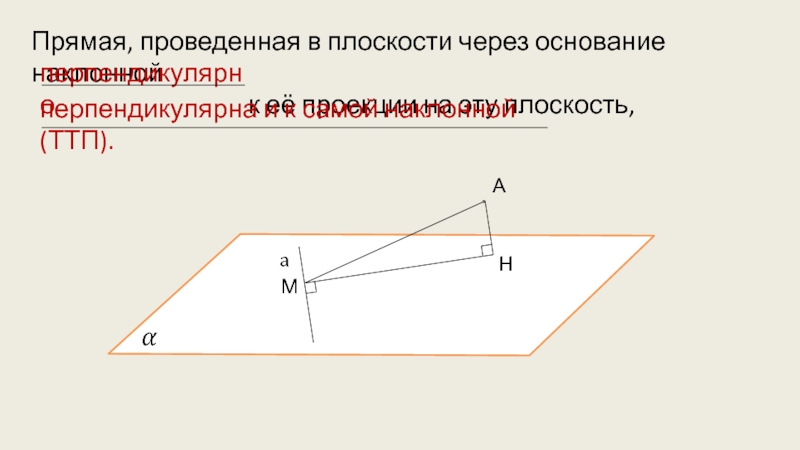
- 8. Прямая, проведенная в плоскости через основание наклонной
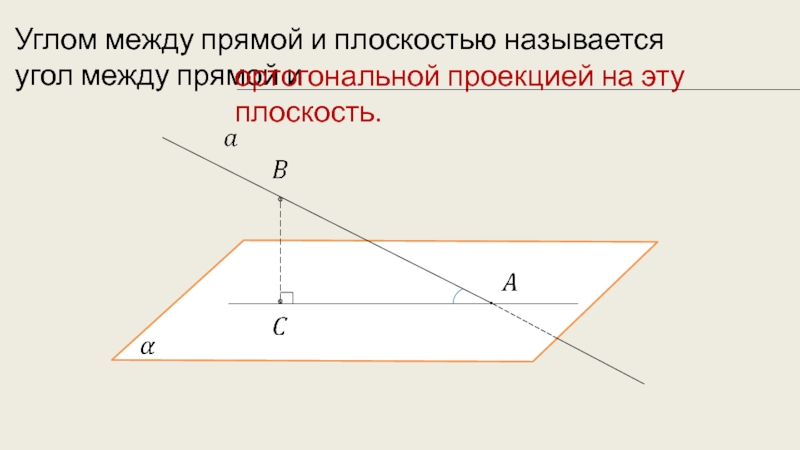
- 9. Углом между прямой и плоскостью называется угол между прямой иортогональной проекцией на эту плоскость.
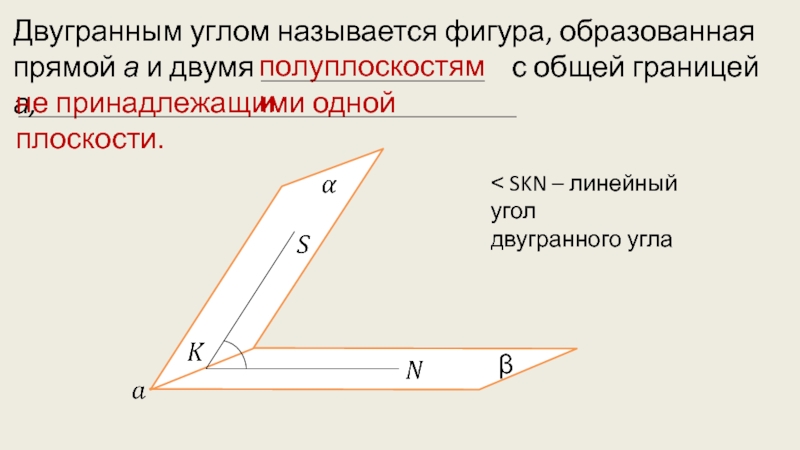
- 10. Двугранным углом называется фигура, образованная прямой а
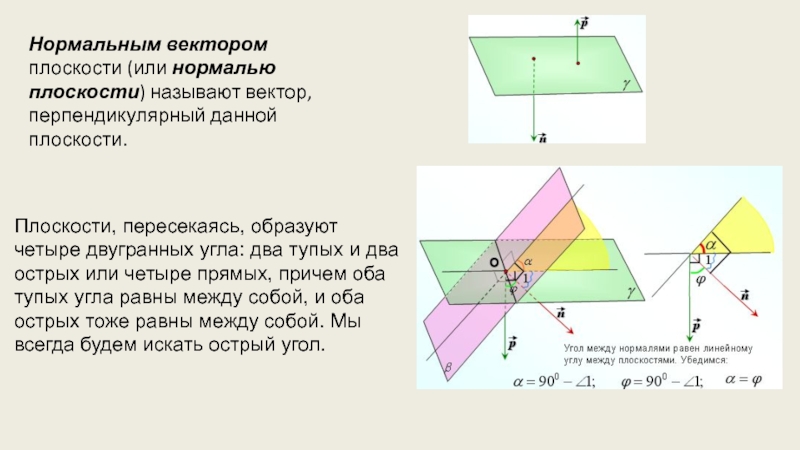
- 11. Нормальным вектором плоскости (или нормалью плоскости) называют
- 12. Угол между векторами вычисляется по формуле:Но при
- 13. Слайд 13
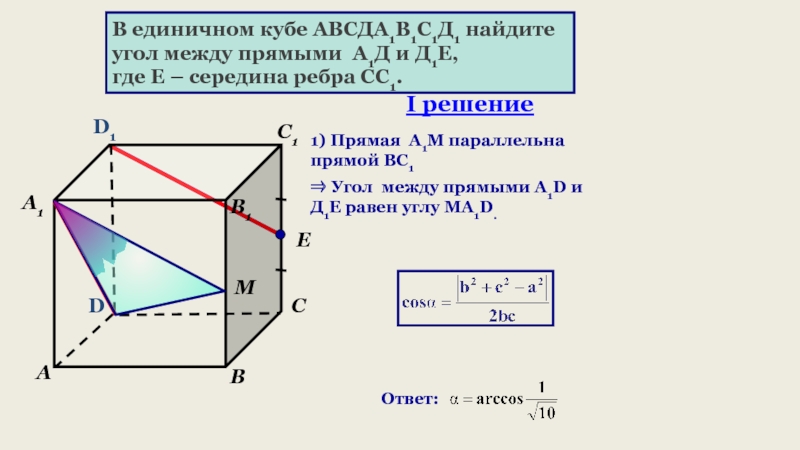
- 14. В единичном кубе АВСДА1В1С1Д1 найдите угол между
- 15. В единичном кубе АВСДА1В1С1Д1 найдите угол между
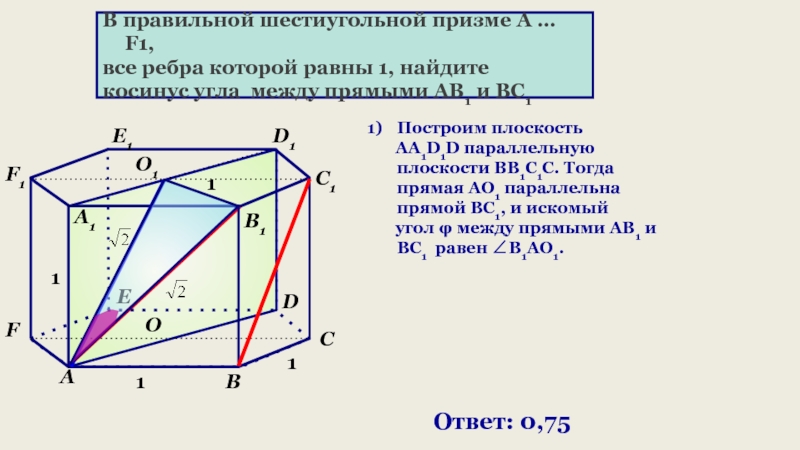
- 16. В правильной шестиугольной призме A … F1,
- 17. В правильной шестиугольной призме A … F1,
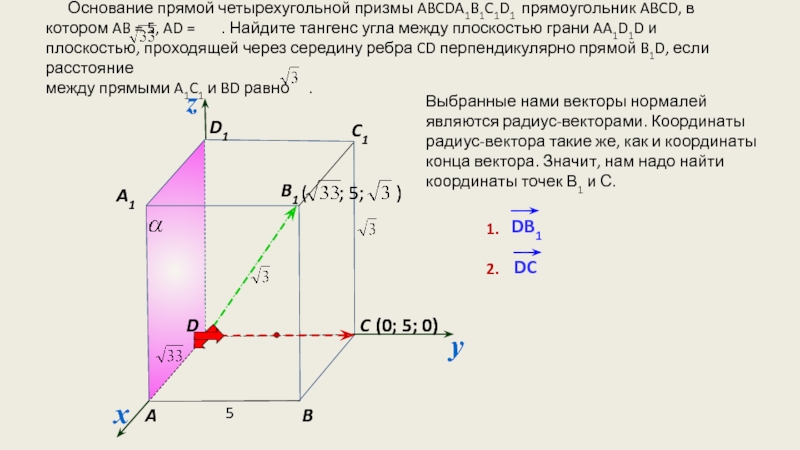
- 18. Основание прямой четырехугольной призмы
- 19. (0; 5; 0) Основание прямой
- 20. Теперь найдем тангенс:
- 21. «Ты скажешь, эта жизнь – одно
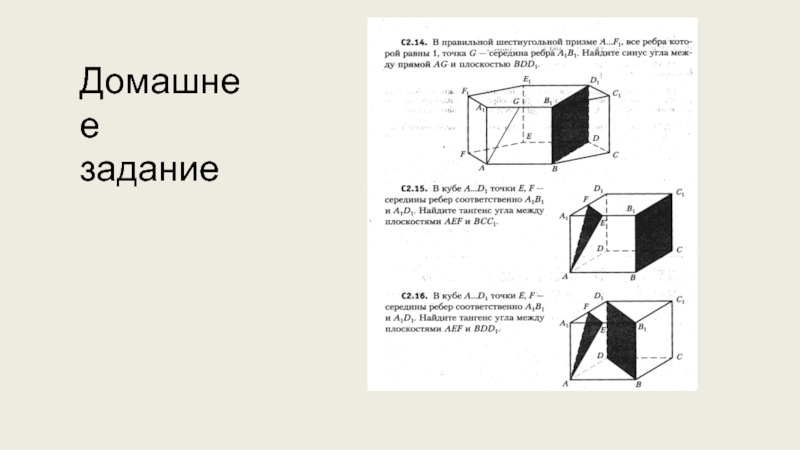
- 22. Домашнее задание
Взаимное расположение прямых в пространстве 1)2)3)аbаbbаПрямые параллельныПрямые пересекаютсяПрямые скрещиваются
Слайд 1Координатный метод решения стереометрических задач при подготовке
к ЕГЭ
А.С. Макаренко «Мастерство-
Слайд 2Взаимное расположение прямых в пространстве
1)
2)
3)
а
b
а
b
b
а
Прямые параллельны
Прямые пересекаются
Прямые скрещиваются
Слайд 5Перпендикуляр, проведенный из данной точки к плоскости, меньше
, проведенной из той же точки к этой плоскости.
любой наклонной
АМ -
АК -
МК -
АК АМ
наклонная
перпендикуляр
проекция
<
Слайд 6Расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости
называется
расстоянием
между параллельными плоскостями.
Слайд 7Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую
прямую параллельно первой, называется
расстоянием между скрещивающимися прямыми.
а
b
А
В
Слайд 8Прямая, проведенная в плоскости через основание наклонной
к её проекции на эту плоскость,
перпендикулярно
перпендикулярна и к самой наклонной(ТТП).
М
А
Н
Слайд 9Углом между прямой и плоскостью называется угол между прямой и
ортогональной проекцией
на эту плоскость.
Слайд 10Двугранным углом называется фигура, образованная прямой а и двумя
с общей границей а,
полуплоскостями
не принадлежащими одной плоскости.
β
˂ SKN – линейный угол
двугранного угла
Слайд 11
Нормальным вектором плоскости (или нормалью плоскости) называют вектор,
перпендикулярный данной плоскости.
Плоскости, пересекаясь, образуют четыре двугранных угла: два тупых и два острых или четыре прямых, причем оба тупых угла равны между собой, и оба острых тоже равны между собой. Мы всегда будем искать острый угол.
Слайд 12Угол между векторами вычисляется по формуле:
Но при решении задач можно выбрать
нормаль так, что угол между векторами будет тупым, а угол между плоскостями не может быть 90°<α<180°. Тогда, чтобы получить косинус острого угла, надо взять полученное числовое значение для косинуса со знаком «–». А лучше применить знак модуля:
Слайд 14В единичном кубе АВСДА1В1С1Д1 найдите
угол между прямыми А1Д и Д1Е,
где Е – середина ребра СС1.
1) Прямая A1М параллельна прямой ВС1
М
Угол между прямыми А1D и Д1Е равен углу МA1D.
I решение
Ответ:
Слайд 15В единичном кубе АВСДА1В1С1Д1 найдите
угол между прямыми А1Д и Д1Е,
где Е – середина ребра СС1.
Ответ:
II решение
1) Введем систему координат, считая началом координат (·) А, осями координат – прямые АВ, АД, АА1.
Слайд 16В правильной шестиугольной призме A … F1,
все ребра которой равны
1, найдите
косинус угла между прямыми AB1 и BC1
косинус угла между прямыми AB1 и BC1
1
1
1
1
Ответ: 0,75
О
О1
Построим плоскость
АА1D1D параллельную плоскости ВВ1С1С. Тогда прямая AO1 параллельна прямой BC1, и искомый
угол φ между прямыми AB1 и BC1 равен B1AO1.
Слайд 17В правильной шестиугольной призме A … F1,
все ребра которой равны
1, найдите
косинус угла между прямыми AB1 и BC1
косинус угла между прямыми AB1 и BC1
1
1
1
1
Ответ: 0,75
II решение
1) Введем систему координат, считая началом координат точку A (0; 0; 0), тогда
Слайд 18 Основание прямой четырехугольной призмы ABCDA1B1C1D1 прямоугольник ABCD, в
котором AB = 5, AD = . Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно .
D1
B
A
D
B1
C1
A1
5
Найдем расстояние между прямыми
A1C1 и BD и решим задачу методом координат.
C
y
Слайд 19(0; 5; 0)
Основание прямой четырехугольной призмы ABCDA1B1C1D1 прямоугольник
ABCD, в котором AB = 5, AD = . Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние
между прямыми A1C1 и BD равно .
между прямыми A1C1 и BD равно .
D1
B
A
D
B1
C1
A1
5
Выбранные нами векторы нормалей являются радиус-векторами. Координаты радиус-вектора такие же, как и координаты конца вектора. Значит, нам надо найти координаты точек В1 и С.
C
y
(0; 5; 0)
Слайд 21 «Ты скажешь, эта жизнь – одно мгновенье Её цени,
в ней черпай вдохновенье
Как проведешь её, так и пройдёт
Не забывай: она - твоё творенье!»
О. Хайям
